Характер движения системы будет существенно зависеть от соотношения между величинами n и k. Здесь различают три случая:
1. n < k. Случай малого сопротивления. Уравнение (5) имеет два различных комплексных корня.
2.n = k. Случай критического сопротивления. Уравнение (5) имеет два кратных
корня.
3.n > k. Случай большого сопротивления. Уравнение (5) имеет два вещественных отрицательных корня.
1. Случай малого сопротивления.
При n < k подкоренное выражение в равенстве (6) отрицательное. Введем обозначение
k1 =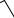 
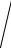k2 −n2
1,2 = – n k1 i
Тогда общее решение уравнения (4) будет иметь вид
q(t) = e–nt (C1cos k1t + C2 sin k1t)
q(t) = A e–nt sin (k1t + )
Движение, определяемое уравнениями (7) или (8), называется затухающими колебаниями
T1 = |
2 |
= |
|
2 |
|
|
|
|
(9) |
|
k1 |
|
|
|
|
|
k 2 − n2 |
Условный период затухающих колебаний – величина постоянная, не зависящая от начальных условий. Так как k1< k, то 2 /k1>2 /k, т.е. условный период затухающих колебаний больше периода собственных колебаний системы при отсутствии сопротивления.
Переменную величину Аe–nt называют условной амплитудой затухающих колебаний.
Для характеристики затухания часто пользуются безразмерной величиной D, которая называется декрементом затухания. Декрементом затухания называется отношение двух
последовательных амплитудных значений обобщенной координаты q, взятых условный период Т1.
Пусть
qi |
= A e |
−nti |
|
|
sin (k1ti + ); |
|
|
|
|
|
qi+1 = A e−n (ti +T1 ) |
sin [(k1ti+T1) + )]= A e−nti e−nT1 |
sin (k1ti+ ); |
Тогда |
D = |
qi |
= enT1 |
|
|
|
. |
|
|
|
|
|
|
|
qi+1 |
|
|
2. Случай критического сопротивления.
При n = k корни 1,2 = – n характеристического уравнения (5) действительные и кратные. При кратных корнях общее решение дифференциального уравнения (4) будет иметь вид
q(t) = e–nt (C1 + C2 t), |
(14) |
Такое движение не имеет никаких признаков периодичности и называется апериодическим движением.
3. Случай большого сопротивления.
При n > k корни характеристического уравнения (5) действительные, различные и отрицательные. Введем обозначение
|
|
|
|
|
|
1,2 = – n k2 |
k2 = |
n |
2 |
− k |
2 |
|
|
|
|
|
|
q(t) = e–nt (C1 |
e−k2t + C |
2 |
e k 2t |
) |
|
|
|
|
|
|
|
|
385 |
|
|
|
|
|
|
|
|
|
3.63. Вынужденные колебания механической системы
без учета сопротивления
Рассмотрим движение механической системы с одной степенью свободы, около положения устойчивого равновесия, когда на точки системы, кроме потенциальных сил, начинают действовать возмущающие силы. При этом обобщенная сила Q(t), характеризующая внешнее воздействие на колебательную систему, изменяется по закону синуса или косинуса:
где Н, р и – соответственно амплитуда, частота и начальная фаза обобщенной силы.
d |
T |
− |
T |
= − |
|
+ Q(t) . |
(2) |
|
|
|
|
|
|
|
|
dt |
q |
|
q |
|
q |
|
|
T = |
1 |
aq |
2 |
; П(q) = |
1 |
сq |
2 |
. |
(3) |
|
|
2 |
|
2 |
|
|
|
|
|
|
T = |
1 |
aq2 |
; |
|
П(q) = |
|
1 |
сq2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
T |
= 0, |
|
T |
= aq, |
|
|
d |
T = aq, |
П |
= сq. |
|
|
|
|
|
|
q |
|
|
|
q |
|
|
|
|
|
|
dt q |
|
|
q |
|
|
|
d |
T |
− |
T |
= − |
|
|
+ Q(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
q |
|
q |
|
|
|
q |
|
|
|
|
q + k2q = hsin( pt + ) |
|
|
|
|
|
|
, |
|
где |
k2 = c/a, h = H/a. |
q(t) = q1 + q2 .
q1 = C1cos kt + C2 sin kt = Asin (kt + ).
Частное решение q2 неоднородного уравнения (4) называют вынужденным колебанием системы. Оно определяется в зависимости от соотношения частот k и p свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (p k)
1. Случай отсутствия резонанса.
В этом случае p k и частное решение q2 следует искать в той же форме, что и правая часть уравнения (5)
В результате подстановка q2 в (5) приводит к соотношению
B(k2 |
– p2) = h, откуда |
B = k2 |
h |
− p2 |
|
|
|
|
q(t) = C1cos kt + C2 sin kt + |
|
|
|
|
|
|
h |
|
|
sin(pt+ ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2 − p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(t) = A1 sin (kt + ) + |
|
|
|
|
|
|
h |
|
|
sin(pt+ ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2 − p2 |
|
|
|
|
|
|
|
|
|
|
|
|
C = q − |
|
h |
sin ; |
C |
|
= |
q0 |
− |
|
|
hp |
cos |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
0 |
k2 |
− p2 |
|
|
|
k k(k |
2 − p2 ) |
|
|
|
|
|
|
|
|
Введем в рассмотрение амплитуду вынужденных колебаний
тогда чисто вынужденные колебания можно представить в следующем виде
q2(t) = A2 sin(pt + + ), |
(14) |
где – сдвиг по фазе вынужденных колебаний относительно колебаний возмущающей
силы. Из (13) и (14) видно, что
=
При p < k фаза вынужденных колебаний совпадает с фазой возмущающей силы. При p > k сдвиг фаз равен , т.е. вынужденные колебания находятся в противоположной фазе по отношению к возмущающей силе.
