
Добавил:
euroduck97
ac3402546@gmail.com
Направление обучения: транспортировка нефти, газа и нефтепродуктов
группа ВН (Вечерняя форма обучения)
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Динамика точки и системы / ДИНАМИКА
.pdf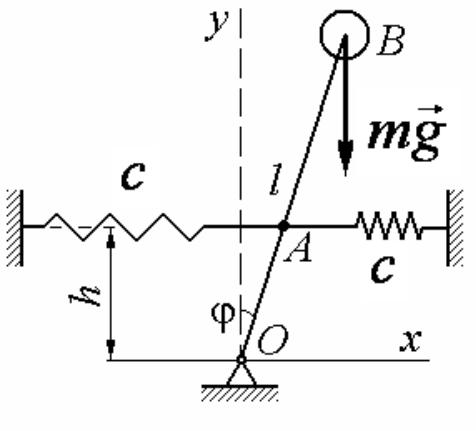
Пример 3.20.
Астатический обращенный маятник. m – масса маятника
l – длина маятника
ОА= h
с – жесткость пружин
q ≡ φ – обобщенная координата
( ) = 1 + 2.
1 = – mg y= – mgl (1 – cos ).
= 2 |
c( xA )2 |
= с(h )2 . |
|
2 |
|||
2 |
363 |
||
|



Потенциальная энергия
|
|
П |
|
2 П |
|
q2 |
|
3 П |
|
q3 |
|||||
П(q) = П0 |
+ |
|
q + |
|
2 |
|
|
|
+ |
|
3 |
|
|
|
+... |
q |
|
2 |
q |
|
6 |
||||||||||
|
|
q |
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П(q) = 1 2 П q2
2 q2 0
|
2 П |
с = const – обобщенный |
||||
с = |
q |
2 |
|
коэффициент жесткости |
||
|
|
0 |
||||
|
|
|
|
|||
|
|
|
|
П(q) = |
1 |
сq2 |
|
|
|
|
|
||
|
|
|
|
2 |
367 |
|
|
|
|
|
|
|
|


Решение:
q(t) = C1cos kt + C2 sin kt.
Произвольные постоянные C1 и C2 определим из начальных условий:
при t = 0 q = q0 и q = q0
C = q ; |
C |
|
|
= |
q0 |
|
||
2 |
|
|||||||
1 |
0 |
|
|
|
k |
|||
|
|
|
|
|
|
|
||
q(t) = q |
cos kt + |
q0 |
sin kt |
|||||
0
k |
370 |
|
Соседние файлы в папке Динамика точки и системы
