Для самостоятельного решения:

Задача 102

Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут досмотр от 7 до 10 автомобилей; б) за пол часа успеет пройти досмотр только 1 автомобиль.

Таможня пройдена, достаём припрятанное:

 Гипергеометрическое распределение вероятностей

Пожалуй, второе по распространённости после биномиального распределения, в котором нет ничего гиперсложного. Да и сложного тоже:

Пусть в совокупности из объектов содержатся объектов, обладающие некоторым признаком. Из этой совокупности случайным образом и без возвращения извлекается n

объектов. Тогда случайная величина X – количество «особых» объектов в выборке –

распределена по гипергеометрическому закону.

С гипергеометрическим законом распределения вероятностей мы неоднократно сталкивались ранее и фактически полностью построили в Задаче 26:

В ящике находится N 20 деталей, среди которых M 5 бракованных. Наудачу извлекаются n 2 детали. Найти вероятность того, что:

а) обе детали будут качественными; б) одна деталь будет качественной, а одна – бракованной; в) обе детали бракованны

По сути дела, здесь фигурирует случайная величина X – количество бракованных деталей в выборке. Прорешаем данную задачу под другим углом зрения, а именно,

бракованных.

1) x1 1

C151 C51 15 5 75 способами можно извлечь 1 качественную деталь и 1 бракованную.

По тому же определению:

бракованными.

Таким образом, закон распределения количества бракованных деталей в выборке:

Контроль: 3821 1538 382 3838 1

Заметьте, что здесь уже предпочтительны обыкновенные дроби – они и точнее и смотрятся лучше.

Теперь разберём более содержательную задачу, в которой я расскажу вам об общих формулах и полезных технических приёмах решения. Как в передаче «Что? Где? Когда?» выносят чёрные ящики, так в теории вероятностей предлагают урны с шарами :)

Задача 103

Из урны, содержащей 6 белых и 4 черных шара, случайным образом и без возвращения извлекают 3 шара.

! Примечание: оговорка «без возвращения» является важной, но её часто опускают, подразумевая этот факт по умолчанию

Составить функцию распределения случайной величины X – числа черных шаров среди выбранных. Найти математическое ожидание и дисперсию этой случайной величины. Построить многоугольник и функцию распределению. Вычислить вероятность

того, что в выборке будет не менее двух чёрных шаров. Вычислить P X M (X ) (X ) .

Как говорится, весь джентльменский набор / полная дамская сумочка.

Кстати, если не нравятся шары, можете представить, что это белые и чёрные котята или…, не знаю, например, красные и чёрные карты.

Решение: поскольку в условии речь идёт о выборке объектов из совокупности и о количестве «особенных» объектов в этой выборке, то предложенная случайная величина имеет гипергеометрическое распределение вероятностей.

Обозначим исходные данные стандартными буквами:

N 6 4 10 – размер совокупности;

M 4 – количество черных шаров в совокупности («особенный» признак); n 3 размер выборки.

Очевидно, что случайная величина X (кол-во чёрных шаров в выборке) может принять следующие значения:

x xi 0, 1, 2, 3

Следует отметить, что этих значений может быть и меньше. В каком случае?

В случае если M n , то есть, если во всей совокупности чёрных шаров МЕНЬШЕ, чем размер выборки. Так, если в урне всего 2 чёрных шара, то значение x3 3 отпадёт.

Для вычисления гипергеометрических вероятностей существует формула, но я вам крайне советую вникать в смысл выполняемых действий.

Сначала вычислим знаменатель дроби:

значение нам потребуется при вычислении каждой вероятности. И каждую вероятность мы вычислим по формуле:

белых шара.

По классическому определению:

шаров.

Результаты лучше записывать в трёх видах: несокращённой обыкновенной дробью, сокращённой обыкновенной дробью и десятичной дробью (с 3-4-5 знаками после запятой). Это упростит решение, и скоро будет понятно, как.

Кроме того, вероятности выгодно и приятно знать заранее. Для этого можно использовать экселевскую функцию =ГИПЕРГЕОМЕТ(x; n; M; N) или сразу воспользоваться Калькулятором (Пункт 8). Едем дальше:

белых шара.

Таким образом, количество чёрных шаров в выборке распределено по следующему закону:

Вероятности записываем обыкновенными дробями!

Контроль: 16 12 103 301 305 1530 309 301 3030 1 , ч.т.п.

В крайнем случае можно использовать десятичные дроби (если обыкновенные сильно наворочены), единственное, нужно следить, чтобы сумма округлённых значений равнялась единице и при необходимости «подгонять» некоторые вероятности. Однако помните, что это уже будет не точным ответом!

Но десятичные значения, безусловно, удобны для построения многоугольника распределения:

Математическое ожидание и дисперсию гипергеометрического распределения можно вычислить в обход общего алгоритма – по специальным формулам:

M ( X ) MN n 104 3 1,2 – среднее количество чёрных шаров в выборке (при многократном повторении таких выборок).

D( X ) MN n ... – мера рассеяния количества чёрных шаров относительно матожидания.

Составим функцию распределения вероятностей. И здесь как раз пригодятся несокращённые обыкновенные дроби. Вычислим накопленные частоты:

p0 12020 16 0,1667 – десятичные значения нужны для ручного построения

графика.

p0 p1 12020 12060 12080 23 0,66667

p0 p1 p2 12020 12060 12036 116120 3029 0,96667 p0 p1 p2 ..

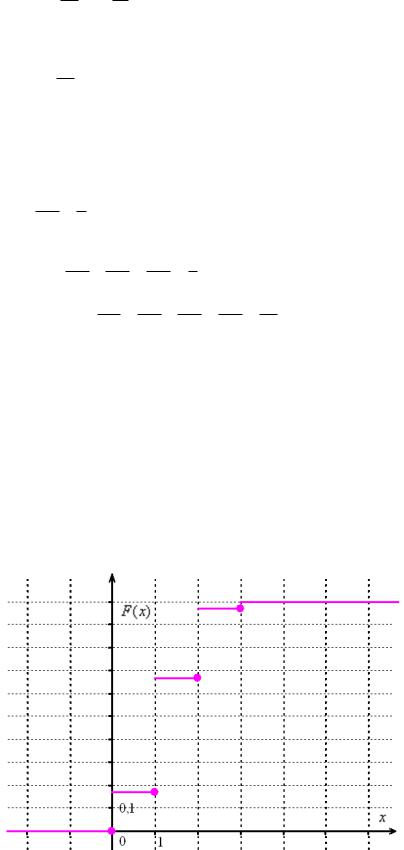
Таким образом, искомая функция:

0 при х 0;

1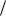6 при 0 х 1; F (x) ... при 1 х 2;

... при 2 х 3;

1 при х 3.

– её значения тоже записываем обыкновенными дробями! Дабы соблюсти точность. Строим график:

Выходим на финишную прямую. Вычислим P X 2 – вероятность того, что в

выборке будет не менее двух чёрных шаров. Это можно сделать не единственным способом. Прямым суммированием вероятностей несовместных исходов:

P X 2 p2 p3 103 301 309 301 1030 13

или с помощью функции распределения и штатной формулы

P(a X b) F (b) F (a) :

P X 2 P(2 X ) F ( ) F (2) 1 23 13

Напоминаю, что здесь существуют критично важные тонкости (см. по ссылке

выше).

И, наконец, рассчитываем стандартную вероятность P X M (X ) (X ) того, что значение случайной величины X отклонится от математического ожидания не более чем на одно среднее квадратическое отклонение (X ) D(X ) 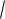0,56 0,75 :

P X M ( X ) ( X ) P ( X ) X M ( X ) ( X )

P M ( X ) ( X ) X M ( X ) ( X )

... F 1,2 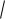0,56 23 16 12

Готово.

Основная трудность гг-распределений состоит в технике вычислений – в них нужно грамотно управляться с дробями, которые частенько получаются страшноватыми.

Это к слову, относится и к другим распределениям – дана где-нибудь вероятность p 32 ,

и, пожалуйста, обыкновенные дроби рулят.

Ну, и конечно, не забываем о том, КАКАЯ ИМЕННО дана случайная величина. Так, в разобранном задании может быть предложена величина X – количество белых шаров в выборке, и тогда решение примет «зеркальный» характер.

Миниатюрная задача для закрепления материала:

Задача 104

В группе из шести студентов два отличника. Наугад выбрали двух человек. Составить закон распределения случайной величины X – число отличников среди выбранных. Найти математическое ожидание и дисперсию. Построить график функции распределения.

Желающие могут решить эту же задачу для случая, когда в группе всего лишь один отличник ;)

…Есть? Отлично!