Добавил:

AAA1 aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский национальный университет радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1-1 Высшая математика / visshaya_matematika_chast_IV

.pdf

Скачиваний:

Добавлен:

31.01.2021

Размер:

10.23 Mб

Скачать

☆

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 3738 / 5638 39 40 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

§8. Основні формули інтегрального числення функцій однієї змінної	371

§8. Основніформулиінтегральногочисленняфункційоднієї змінної

І. Невизначений інтеграл

Основна таблиця інтегралів

xα dx =

xα +1

+ C , ( α ≠ −1), 1 dx = dx = x + C .

∫

∫dx

= ln

+ C .

∫ax dx =

+ C

, ( a > 0, a ≠ 1).

ln a

4.∫ex dx = ex + C .

5.∫cos x dx = sin x + C .

6.∫sin x dx = −cos x + C .

7.∫cosdx2 x = tg x + C .

8.∫sindx2 x = −ctg x + C .

9.	∫	dx	= arcsin x + C .
		1− x2
10.	∫	dx	= arcsin	x	+ C .
		a2 − x2		a

11.∫1+dxx2 = arctg x + C .

12.∫a2dx+ x2 = a1 arctg ax + C .

13. ∫	2dx	2	=	1	ln	a + x	+ C .

				2a		a − x
a	− x

372	Глава 7. Довідковий матеріал

14.

= ln

x +

x2 ± a2 + C .

∫ x2 ± a2

15.

∫

x dx

= x2 ± a2 + C .

x2 ± a2

16.

∫ dx

= ln

+ C .

sin x

∫

17.

= ln

+ C .

cosx

18.∫tg x dx = −ln cosx + C .

19.∫ctg x dx = ln sin x + C .

20.∫sh x dx = ch x + C .

21.∫ch x dx = sh x + C .

22.∫chdx2x = th x + C .

23.∫shdx2x = −cth x + C .

Заміна змінної

f (x) dx =

x = ϕ (t)

= f (ϕ (t)) ϕ ′(t) dt .

∫

dx = ϕ ′(t) dt

∫

Інтегрування частинами

∫

u dv = uv −

v du .

Інтегрування найпростіших дробів

1) ∫ A

dx = A ln

x − a

+ C .

x − a

2) ∫

+ C .

− k (x − a)

k −1

(x − a)

B − A

Ax + B

x + 2

3) ∫ 2

dx =

ln(x

+ px + q) +

arctg

+ C .

+ px + q

q −

§8. Основні формули інтегрального числення функцій однієї змінної

373

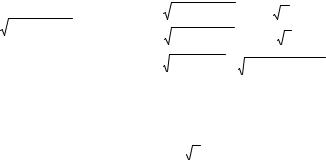
Ax + B

dx =

A (t2 + a2 )−k+1

+ B − A

Ik , де

∫(x2 + px

+ q)k

− k +1

= t −

dx = dt

∫(x2 + px + q)k

∫(t

+ a2 )k

q −

= a2

> 0

2k − 3

Ik−1, k > 1 .

2a2 (k −1) (t2 + a2 )k−1

a2 2k − 2

При k = 1: I =

arctg

+ C .

∫t2 + a2

Інтегрування ірраціональних функцій

Інтеграл

Підстановка

r 1

r 2

x = tk ,

де k – загальний знаменник

∫R x, x

, x

,…, x

дробів

, i

= 1, n .

r 2

ax + b

= tk ,

ax+b

cx + d

∫R

,…,

де k – загальний знаменник

cx+d

дробів

, i

= 1, n .

Підстановки Ейлера:

а) ax2

+ bx + c = t ± x a , a > 0 ;

∫R x,

+ bx + c

б) ax

+ bx + c = x t ± c , c > 0 ;

в) ax2 +bx+c

= a (x − x )(x − x ) =

= t (x − x1 ) .

Диференціальний

біном

∫xm (a + bxn ) p dx

а)

p – ціле число

а) t = s

x , де s – загальний

знаменник дробів m і n

374	Глава 7. Довідковий матеріал

б)

m +1

– ціле число

б) a + bxn

= ts , де s – знаменник

дробу p

в)

m +1

+ p – ціле число

в) ax−n + b = t s , де

s – знамен-

ник дробу p

Інтегрування тригонометричнихфункцій

t =tg

∫R(sin x, cos x) dx

;

sin x =

; cos x =

1− t2

+ t2

∫R(sin x, cos x) dx , де:

а)

R(−sin x, cos x) = −R(sin x, cos x) ;

t = cos x ;

б)

R(sin x, − cos x) = −R(sin x, cos x) ;

t = sin x ;

в)

R(−sin x, − cos x) = R(sin x, cos x)

t = tg x

∫R(tg x)dx

t = tg x

∫R(sin

t = tg x ;

x, cos

x) dx ,

sin2 x =

; cos2

x =

n , m – парні, хоча б одне з них

+ t2

1+ t2

від’ємне

∫R (sinn x, cosm x) dx ,

sin2 x =

1− cos 2x

; cos2

x =

1+ cos 2x

n = 2k , m = 2 p

∫cos mx cos nx dx

cosmxcosnx =

[cos(m + n)x + cos(m − n)x]

∫sin mx cos nx dx

sin mxcosnx = 12[sin (m + n)x + sin (m − n)x]

∫sin mx sin nx dx

sin mxsin nx =

[cos(m − n)x − cos(m + n)x]

Тригонометричні підстановки

− x

x = asint

або x = a cos t

∫R x,

+ x

x = a tg t або x = a ctg t

∫R x,

R x,

− a

cost

∫

; cth2 x −1 =

; ch2 x =

ch 2x +1 2

§8. Основні формули інтегрального числення функцій однієї змінної	375

Інтегрування гіперболічних функцій

Аналогічно інтегруванню тригонометричних функцій з урахуванням формул:

sh2 x =

1− th2

ch2 x − sh2 x = 1 ; ch2 x + sh2 x = ch2x ; 2sh x ch x = sh 2x ;

ch 2x −1 2

x = 1 ch2 x

;

sh2 x

ІІ. Визначений інтеграл

Формула Ньютона-Лейбніца

ba = F(b) − F(a)

∫f (x) dx = F(x)

Заміна змінної

x = ϕ

(t), dx = ϕ ′(t) dt

f [ϕ (t)]ϕ ′(t) dt

f (x) dx =

∫

ϕ (α )

= a,

ϕ (β )

= b

∫

Інтегрування частинами

udv = uv

− v du

∫

ІІІ. Застосування визначеного інтеграла

Площа плоскої фігури D

Декартова система координат

D : y = f (x), f (x) ≥ 0,

x = a, x = b, y = 0 .

S = ∫f (x) dx

D : y = f1(x), y = f2 (x),

f1(x) ≤ f2 (x),

S = ∫[ f2 (x) − f1 (x)]dx

x = a, x = b, a ≤ b .

Полярна система координат

D : ρ = ρ (ϕ ), α ≤ ϕ ≤ β .

S = 21 ∫ρ 2 (ϕ )dϕ

376	Глава 7. Довідковий матеріал

Параметричне задання

D : y = f (x), x [a,b],

x = x (t),

y = y(t), α ≤ t ≤ β .

x = x (t),

y = y(t),

S = ∫y(x) dx = dx = x′(t)dt,

ax = a, t = α , x = b, t = β .

= ∫y(t)x′(t)dt

Довжина кривої L

Декартова система координат			b
L : y = f (x), a ≤ x ≤ b .			l = ∫ 1 + y′2 (x) dx
			a
Полярна система координат			β
L : ρ = ρ (ϕ ), α ≤ ϕ ≤ β .			l = ∫ ρ 2 (ϕ ) + ρ ′2 (ϕ ) dϕ
			α
Параметричне задання
	L R2		β
	x = x (t),		β	2			2
	x = x (t),	α ≤ t ≤ β ;	l = ∫ x′	2	(t) + y′		2	(t) dt
L :	y = y(t),	α ≤ t ≤ β ;	l = ∫ x′		(t) + y′			(t) dt
	y = y(t),		α
	L R3
x = x (t),
	y = y(t), α ≤ t ≤ β .		β
L :	y = y(t), α ≤ t ≤ β .		l = ∫ x′2 (t) + y′2 (t) + z′2 (t) dt
	z = z(t),		α
	z = z(t),		α
	Об’єм тіла за площами паралельних перерізів
S(x) – площа перерізутіла					b
площиною, перпендикуляр-			V = ∫S(x) dx
ною осі Ox , a ≤ x ≤ b					a
ною осі Ox , a ≤ x ≤ b

		Об’єм тіла обертання
Декартова система координат						b
D : y = f (x), y = 0, x = a, x = b,			Vx = π ∫y2 (x)dx
вісь обертання – Ox						a
вісь обертання – Ox
D : y1 = f1(x), y2 = f2 (x),			b
0 ≤ f1(x) ≤ f2 (x),			b		2	(x) −		2	(x)]dx
0 ≤ f1(x) ≤ f2 (x),					2			2
	x = a, x = b,		Vx = π ∫[ f2				f1
	x = a, x = b,		a
вісь обертання – Ox
D : x = ϕ ( y), x = 0, y = c, y = d,						d
вісь обертання – Oy			Vy = π			∫ϕ 2 ( y)dy
						c

§8. Основні формули інтегрального числення функцій однієї змінної

377

D : x1 = ϕ 1( y), x2 = ϕ 2 ( y),

0 ≤ ϕ 1 ( y) ≤ ϕ 2 ( y),

Vy = π ∫[ϕ

( y)]dy

y = c, y = d,

( y) − ϕ 1

вісь обертання – Oy

Полярна система координат

D : ρ = ρ (ϕ

V =

∫ρ

3 (ϕ ) sinϕ dϕ

ϕ 1 = α , ϕ 2 = β (α < β )

Площа поверхні обертання

Декартова система координат

l : y = f (x) ≥ 0, a ≤ x ≤ b .

Px = 2π ∫f (x) 1+ f ′2 (x) dx

Полярна система координат

l : ρ

= ρ (ϕ ), α ≤

ϕ ≤ β .

= 2π ∫ρ sinϕ

ρ 2 (ϕ ) + ρ ′2 (ϕ

) dϕ

Параметричне задання

x = x (t),

α ≤

t ≤ β ;

Px = 2π ∫y(t) x′2 (t) + y′2 (t) dt

l :

y = y(t),

Статичні моменти плоскої кривої l

відносно координатних осей

l : y = f (x), a ≤ x ≤ b ;

відносно осі Ox

M x = ∫f (x) 1 + f ′2 (x) dx

l : y = f (x), a ≤ x ≤ b ;

відносно осі Oy

M y = ∫x

1 + f ′2 (x) dx

Статичні моменти плоскої фігури D відносно координатних осей

D : y = f (x), y = 0, x = a, x = b ;

відносно осі Ox

M x =

f 2 (x) dx

∫a

D : y = f (x), y = 0, x = a, x = b ;

відносно осі Oy

M y

= ∫x f (x) dx

Моменти інерції плоскої кривої l

відносно координатних осей

l : y = f (x), a ≤ x ≤ b ;

відносно осі Ox

I x = ∫f 2 (x) 1 + f ′2 (x) dx

l : y = f (x), a ≤ x ≤ b ;

відносно осі Oy

I y = ∫x2

1 + f ′2 (x) dx

378	Глава 7. Довідковий матеріал

Моменти інерції плоскої фігури D відносно координатних осей

D : y = f (x), y = 0, x = a, x = b ;

відносно осі Ox

I x

f 3 (x) dx

3 a∫

D : y = f (x), y = 0, x = a, x = b ;

відносно осі Oy

I y = ∫x2 f (x) dx

Координати центра ваги плоскої кривої l

= M y

∫x 1 + f ′2 (x) dx

= a

∫ 1 + f ′2 (x) dx

l : y = f (x), a ≤ x ≤ b

M x

∫f (x) 1 + f ′2 (x) dx

yc =

= a

∫ 1 + f ′2 (x) dx

Координати центра ваги плоскої фігури D

M y

∫x f (x) dx

∫f (x) dx

D : y = f (x), y = 0, x = a, x = b

M x

∫f 2 (x) dx

2∫f (x) dx

Робота змінної сили F = F(x)

a ≤ x ≤ b

A = ∫F(x) dx

§8. Основні формули інтегрального числення функцій однієї змінної

379

ІV. Невласні інтеграли

Невласні інтеграли І роду

+∞

∫f (x) dx ;

∫f (x) dx;

Типи

−∞

+∞

∫

f (x) dx

∫

f (x) dx +

f (x) dx, c R

−∞

+∞

Означення

∫

f (x) dx = lim

f (x) dx , інтеграл збігається за умови

b→∞

∫

існування скінченної границі справа

+∞

a+∞ = F(+∞ )− F(a) ,

Обчислення

∫f (x) dx = F(x)

F(+∞ )=

lim F(x) ,

x→+∞

F(x)

– первісна функції

f (x)

на проміжку [a, + ∞

)

+∞

∫f (x) dx

(1)

∫g(x) dx

(2)

1) 0 ≤ f (x)≤ g(x) x +[a∞,

)

Ознаки

а) інтеграл (2) збіжний

інтеграл (1) збіжний;

б) інтеграл (1) розбіжний

інтеграл (2) розбіжний;

порівняння

2) f (x) > 0, g(x) > 0 x [a+,∞ )

lim

f (x)

A> 0

інтеграли (1), (2) обидва

g(x)

x→+∞

збігаються або обидва розбігаються

Інтеграл для

+∞

−

збігається, якщо p >1,

порівняння

∫1

p ≤

розбігається, якщо

f (x)

– знакозмінна функція на проміжку [a, + ∞ )

+∞

Достатня ознака

∫f (x) dx

(1)

∫

f (x)

(2)

порівняння

інтеграл (2) збігається

інтеграл (1) збігається

380	Глава 7. Довідковий матеріал

	+∞
Абсолютно	∫f (x) dx – абсолютно збіжний,
збіжний	a
збіжний		+∞
інтеграл		+∞
	якщо	∫	f (x)	dx – збіжний


		a
	+∞
Умовно	∫f (x) dx – умовно збіжний,
збіжний	a
інтеграл		+∞			+∞
	якщо	∫	f (x)	dx – розбіжний, а	∫f (x) dx – збіжний
	якщо

		a			a

Невласні інтеграли ІІ роду

	b
	∫f (x) dx , x = a		– особлива точка функції			f (x) ,
	a
	lim f (x) = ∞ ;
	x→ a
	b
Типи	∫f (x) dx , x = b – особлива точка функції					f (x) ,
	a
	lim f (x) = ∞ ;
	x→ b
	b	c	b
	f (x) dx = f (x) dx + f (x) dx , x = c , a < c < b –
	∫	∫	∫
	a	a	c
	особлива точка функції f (x) ,				lim f (x) = ∞
					x→ c
	b		b
	∫f (x) dx = lim		∫f (x) dx , де		x = a – особлива точка
Означення	a	ε→+ 0 a+ε
	функції f (x) . Інтеграл збігається за умови існування
	скінченної границі справа
		b		ba+0 = F(b) − F(a + 0) ,
Обчислення		∫f (x) dx = F(x)


		a	F(a + 0) = lim F(x) ,
			F(a + 0) = lim F(x) ,
				x→ +a 0
	F(x)	– первісна функції f (x)			на проміжку (a, b] ,
	x = a	– особлива точка функції f (x)

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 3738 / 5638 39 40 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

Соседние файлы в папке 1-1 Высшая математика

#
31.01.202141.44 Кб55325.jpg
#
31.01.202110.43 Кб56Individual work 1.pdf
#
31.01.202187.04 Кб56Individual work 2.doc
#
31.01.202153.25 Кб66REKOMENDOVANA_LITERATURA-1.doc
#
31.01.202128.67 Кб56Titul.doc
#
31.01.202110.23 Mб87visshaya_matematika_chast_IV.pdf
#
31.01.2021539.08 Кб55ВМ - график консультаций.jpg
#
31.01.2021458.12 Кб55ВМ - для идиотов.jpg