6.6. Модифицированный алгоритм Роббинса-Монро

Множественная определенность априорной информации о cистеме охватывает случай, когда известны только диапазоны (6.2) изменения диагностических параметров для работоспособного состояния. В реальных ситуациях этот случай имеет место, когда:

- системы еще только находятся в стадии разработки, а к моменту ввода их в эксплуатацию необходимо, чтобы средства диагностирования были готовы к применению;

- системы уже эксплуатируются, но в единичных экземплярах и непродолжительное время.

В этих ситуациях объем и качество априорной информации о системе могут оказаться недостаточными даже для приближенной оценки диапазонов изменения диагностических параметров при различных отказах. В этом случае наиболее конструктивным является подход, основанный на информации о фактах выхода значений диагностических параметров за допустимые интервалы (6.2).

При реализации такого подхода используются бинарные значения диагностических параметров, которые определяются выражением

(6.67)

Тогда в качестве G-преобразования может применяться ортогональная система функций вида (6.11), компоненты которой задаются выражением

, , (6.68)

где – дельта-функция (символ Кронекера).

Пример 6.4. Выполнить G-преобразование наблюдаемого состояния

. (6.69)

Поскольку вектор (6.69) имеет пять координат ( ), ортогональная система (6.11) принимает вид

. (6.70)

Из выражения (6.68) следует, что координатные функции вектора (6.70) определяются следующим образом:

; ;

; ; .

Тогда

.

▲

Очевидно, что в общем случае вектор диагностических параметров в бинарной форме (или вектор бинарных признаков) представляется как

. (6.71)

Вектор (6.71) называется наблюдаемым состоянием системы в бинарной форме.

Обучающая выборка вида (6.5) в случае бинарного представления диагностических параметров записывается как

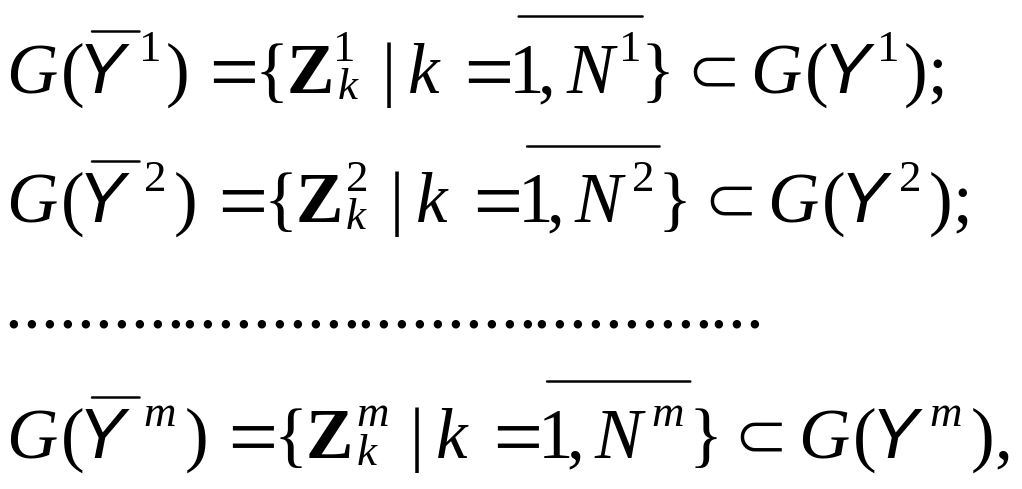(6.72)

где ,  – подмножество G-преобразованных наблюдаемых состояний, представляющее i-й отказ системы; – мощность обучающей выборки по i-му отказу.

Аппроксимирующая функция (6.12) записывается в форме

. (6.73)

Рекуррентные соотношения (6.18) для реализации процесса обучения принимают вид

, , (6.74)

а для каждой координаты вектора E_i соотношения представляются как

, . (6.75)

Изображения, полученные в результате обучения на основе выборки (6.72), имеют форму (6.6):

, . (6.76)

При этом как и в случае G-преобразования на основе ортогонального тригонометрического базиса (6.21) значения координат в выражении (6.76) ограничиваются интервалом , но их содержание будет принципиально иным.

Положительное значение координаты вектора (6.76) указывает на то, что в обучающей выборке (6.72) преобладают такие наблюдаемые состояния, при которых значения j-го диагностического параметра при i-м отказе системы не выходят за допустимый интервал (6.2), и наоборот в случае отрицательного значения.

В рассматриваемом контексте всякая координата в (6.76) представляется как произведение

. (6.77)

Первый сомножитель в выражении (6.77) представляет собой обобщенный символ

, (6.78)

где - функция, которая задается следующим образом [7]:

. (6.79)

Применение функции (6.79) означает, что символ (6.78) имеет два возможных значения: .

Второй сомножитель в (6.77) представляет весовое значение символа (6.78):

. (6.80)

Cимвол выполняет роль индикатора попадания (или непопадания) j-го диагностического параметра в допустимый интервал (6.2). Совокупность обобщенных символов образует вектор

, (6.81)

который является наблюдаемым состоянием в бинарной форме при i-м отказе системы.

Вес ( ) в данном случае может трактоваться как вероятностная оценка принадлежности (или не принадлежности) значения j-го диагностического параметра допустимому интервалу (6.2).

Например, означает, что j-й диагностический параметр выходит за допустимый интервал при i-м отказе системы с вероятностью 0,81. Выход из допустимого интервала указывает на отрицательное значение индикатора ( ) в формуле (6.78), а его вес (6.80) составляет .

На множестве всевозможных элементов вида (6.71), (6.76) порождается структура n-мерного евклидова пространства Z, каждая координата которого ограничена интервалом . Расстояние между элементами в данном пространстве также будет обозначаться через ρ. Например, расстояние между наблюдаемым состоянием (6.71) системы и изображениями (6.76) задается формулой

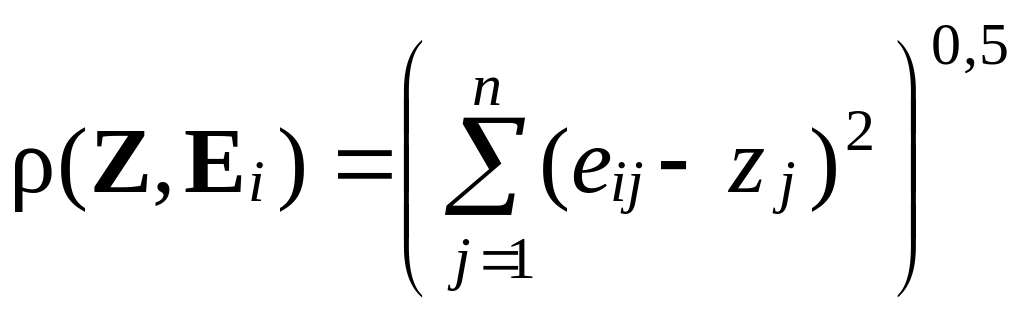, . (6.82)

Очевидно, что результатом обучения с применением тригонометрического базиса (6.21) являются координаты изображения в виде таких абстрактных величин, которым не представляется давать вероятностную интерпретацию.

Из предварительного сравнения подходов к построению изображений на основе первого и второго вариантов множественной определенности априорной информации о системе (подразд. 6.4 и настоящий подраздел) может показаться, что подход на основе второго варианта имеет преимущество. Прежде всего, подобный вывод напрашивается вследствие того, что координаты изображения (6.76) характеризуются весовыми значениями в виде вероятностных оценок. Это упрощает анализ полученной модели распознавания технических состояний.

Однако следует иметь в виду, что преобразование (6.67) ведет к огрублению имеющейся информации по отказам системы. На рис. 6.1 показаны интервалы изменения произвольного диагностического параметра, которым соответствует отрицательное или положительное значения бинарного признака.

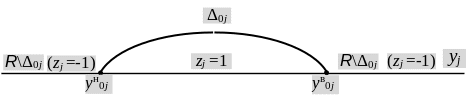
Из рис.6.1 видно, что вне зависимости от величины диагностического параметра в рамках интервала значение бинарного признака одно и то же . Кроме того, в случае выхода диагностического параметра за допустимый интервал ( или, что равносильно ) не учитывается с какой стороны (слева или справа) от на вещественной оси находится значение данного параметра и на каком расстоянии от оно находится. В данном случае бинарный признак имеет значение . Указанные причины свидетельствуют, что подход, основанный на бинарном представлении диагностических параметров, следует применять, когда другие подходы неприменимы.

Пример 6.4. Пусть наблюдаемое состояние системы определяется вектором

. (6.83)

Сформирована обучающая выборка (6.72) для i-го отказа ( ):

, , , , , , (6.84)

, , , , , .

Номер образа в выборке (6.84) совпадает с номером шага обучения, на котором данный образ используется: .

Требуется построить изображение i-го отказа, используя все элементы выборки.

Из (6.20) и (6.68) следует, что первый шаг обучения представляется выражением

.

Начиная со второго шага обучающая процедура реализуется на основе выражения (6.74):

;

.

Таким же образом выполняются последующие шаги обучающей процедуры. Промежуточные и конечные результаты обучения сведены в табл.6.4.

Таблица 6.4

Промежуточные и конечные результаты обучения на основе выборки (6.84)

Zi(1)	Ei(1)	Zi(2)	Ei(2)	Zi(3)	Ei(3)	Zi(4)	Ei(4)
1	1	-1	0	1	0,33	1	0,50
-1	-1	-1	-1	1	-0,33	-1	-0,50
1	1	-1	0	-1	-0,33	-1	-0,50
1	-1	-1	-1	1	-0,33	-1	-0,50
Zi(5)	Ei(5)	Zi(6)	Ei(6)	Zi(7)	Ei(7)	Zi(8)	Ei(8)
1	0,60	1	0,67	1	0,71	1	0,75
-1	-0,60	-1	-0,67	-1	-0,71	-1	-0,75
1	-0,20	-1	-0,33	1	-0,14	1	0,00
1	-0,20	1	0,00	-1	-0,14	-1	-0,25
Zi(9)	Ei(9)	Zi(10)	Ei(10)	Zi(11)	Ei(11)	Zi(12)	Ei(12)
1	0,78	1	0,80	1	0,82	1	0,83
-1	-0,78	-1	-0,80	-1	-0,82	-1	-0,83
1	0,11	1	0,20	1	0,27	1	0,33
-1	-0,33	-1	-0,40	-1	-0,45	-1	-0,50

Из табл.6.4 следует, что, например, восьмой шаг обучающей процедуры определяется выражением

.

Заключительным шагом процесса обучения является двенадцатый:

.

В соответствии с (6.29) в качестве оптимального принимается изображение, полученное на заключительном шаге:

. (6.85)

▲

Необходимо отметить, что в случае применения модифицированного алгоритма Роббинса-Монро также может быть реализована процедура группировки обучающих образов и ранжирования групп (подразд.6.5).

1 В соответствии с обозначениями, принятыми в разд.2, через m обозначается мощность множества отказов системы.

1¹ Понятия ортогональной системы и ортогонального базиса даются в приложении 2.