6.5. Процедура группировки обучающих образов и ранжирования групп

Анализ структуры рекуррентных соотношений показывает, что по мере увеличения числа шагов значимость обучающих образов для формируемого изображения снижается. Указанный факт связан с тем, что коэффициент в соотношениях (6.18) на предыдущем шаге обучения больше, чем на последующем. Поэтому каждый предыдущий образ более значим, чем последующий. Если на начальных шагах обучения используются типичные образы для данного отказа, то увеличивается скорость сходимости процесса обучения к оптимальному вектору [18].

Понятие скорости сходимости может быть дано при сравнении двух вариантов процесса обучения, которые реализуются с различной последовательностью использования элементов выборки. Тот вариант, при котором требуется меньше обучающих образов для достижения заданного условия насыщения (т.е. выполнения неравенства (6.30) или (6.31) при фиксированном значении или ), характеризуется большей скоростью сходимости. Представляется, что в качестве показателя изменения скорости сходимости процесса обучения целесообразно использовать относительную величину

, (6.39)

где – количество элементов выборки, не использованных при обучении (из общего числа ).

Величина (6.39) позволяет сравнивать изменение (в процентах) скорости сходимости различных вариантов процесса обучения на основе одной и той же выборки.

Одним из возможных способов повышения скорости сходимости является группировка обучающих образов и ранжирование полученных групп для определения очередности их использования в процессе обучения.

При группировке рассматривается выборка по i-му виду технического состояния [см. (6.5)]:

. (6.40)

Пусть J – индексное множество обучающих образов из ( , где – мощность множества J). На первом этапе в выборке (6.40) необходимо найти подмножество эквивалентных (неразличимых) между собой элементов. Обучающие образы следует считать эквивалентными, если расстояние между ними по метрике евклидова пространства Y не превышает погрешности δ их регистрации в контрольных точках системы:

, (6.41)

где 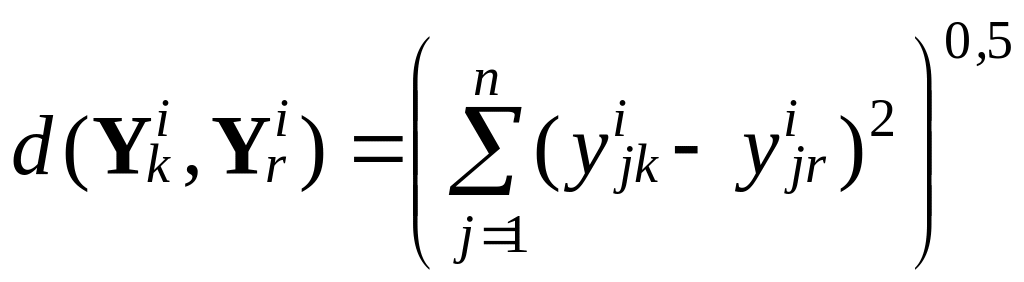– расстояние между и в пространстве Y.

Для определения такого подмножества в выборке (6.40) выделяется произвольное наблюдаемое состояние , которое рассматривается как эталонное для . Затем находится группа элементов

, , (6.42)

находящихся в замкнутой окрестности наблюдаемого состояния c радиусом :

. (6.43)

Под замкнутой окрестностью в данном случае понимается шар в евклидовом пространстве Y c центром в точке . Граничные точки шара охватываются окрестностью, в связи с этим неравенство (6.43) является нестрогим. Поскольку диаметр шара равен δ, в дальнейшем такая окрестность называется δ-окрестностью элемента и обозначается .

Элементы подмножества (6.42) совместно с эталоном находятся в окрестности и образуют группу эквивалентных обучающих образов:

, (6.44)

где – индексное множество эквивалентных обучающих образов первой группы, ; – мощность подмножества (6.44), .

Очевидно, что для любой пары элементов и из группы (6.44) условие (6.41) выполняется. Если имеет место предельный случай данного условия ( ), это свидетельствует, что элементы и принадлежат множеству граничных точек окрестности и находятся на противоположных концах какого-либо ее диаметра.

При (или ) группировка носит вырожденный характер, так как вся обучающая выборка (6.40) представляет собой одну группу эквивалентных образов. Когда

, (6.45)

следует переходить ко второму этапу группировки. На данном этапе анализируется разность множеств и , т.е. подмножество

. (6.46)

В (6.46) выделяется произвольный элемент , который рассматривается как эталонный для данного подмножества. Находится группа элементов

, , (6.47)

которые эквивалентны :

. (6.48)

Элементы подмножества (6.47) совместно с эталоном находятся в окрестности и образуют группу эквивалентных обучающих образов:

, (6.49)

где – индексное множество эквивалентных обучающих образов второй группы, ; – мощность подмножества (6.49), .

При (или ) обучающая выборка (6.40) состоит из двух групп эквивалентных элементов. Когда

, (6.50)

осуществляется переход к третьему этапу группировки. На данном этапе рассматривается подмножество

. (6.51)

В (6.51) выделяется произвольный элемент , который рассматривается как эталонный для данного подмножества. Находится группа элементов

, , (6.52)

которые эквивалентны : .

Элементы подмножества (6.52) совместно с эталоном находятся в окрестности и образуют группу эквивалентных обучающих образов:

, (6.53)

где – индексное множество эквивалентных обучающих образов третьей группы, ; – мощность подмножества (6.53), .

При реализуется следующий этап группировки.

Таким же образом формируются все остальные группы эквивалентных обучающих образов. На заключительном этапе рассматривается подмножество

. (6.54)

В (6.54) выделяется произвольный элемент , который рассматривается как эталонный для данного подмножества. Все элементы группы

, (6.55)

эквивалентны :

.

Элементы подмножества (6.55) совместно с эталоном находятся в окрестности и образуют группу эквивалентных обучающих образов:

. (6.56)

В выражении (6.56) индексное множество эквивалентных обучающих образов p-й группы определяется как

, (6.57)

где – мощность подмножества (6.56).

Равносильной записью выражения (6.57) является

. (6.58)

Равенства (6.57) и (6.58) указывают на то, что выборка (6.40) разбита на группы эквивалентных обучающих образов, а подмножества (6.54) и (6.56) совпадают между собой:

.

После того как все группы сформированы, они ранжируются. Пусть

. (6.59)

В неравенствах (6.59) мощность групп снижается по мере возрастания их номеров. Соотношения между мощностью могут быть и другие, но в любом случае ранжирование выполнимо с присвоением группам номеров в порядке их возрастания.

Таким образом, результаты группировки обучающих образов и ранжирования полученных групп можно представить в следующем виде:

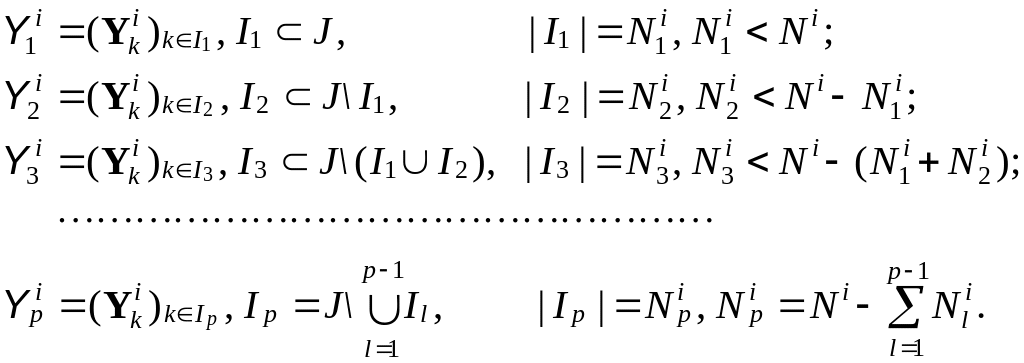(6.60)

Указанные действия выполняются для каждого подмножества ( ) из обучающей выборки (6.5).

Фактически выражения (6.60) означают задание на множествах обучающих образов по всем отказам отношений эквивалентности ( ), которые обеспечивают объединение в рамках одной группы эквивалентных элементов. В результате для обучающей выборки по каждому отказу формируется упорядоченное фактор-множество

, . (6.61)

Элементами фактор-множества являются полученные группы обучающих образов. Порядок использования групп в процессе обучения совпадает с их номером (рангом) в выражении (6.61). Последовательность применения данных образов в рамках одной и той же группы произвольна. Таким образом, при выполнении группировки обучающих образов и ранжировании групп изображение на первом шаге формируется не в соответствии с условием (6.20), а на основе выражения

, . (6.62)

Равенство (6.62) указывает, что в качестве берется произвольный элемент первой группы после его G-преобразования.

Пример 6.3. Рассматривается обучающая выборка из примера 6.2. Требуется выполнить группировку обучающих образов и ранжирование групп при , а также провести обучение на основе полученных результатов.

Пусть в качестве эталонного обучающего образа принимается , т.е. . Тогда условие (6.43) запишется как

. (6.63)

Расстояния между и другими элементами обучающей выборки показаны в табл.6.2.

Таблица 6.2