6.3. Схема итеративного градиентного поиска. Алгоритм Роббинса-Монро

На математическом уровне метод стохастической аппроксимации сводится к схеме итеративного градиентного поиска.

Данная схема применительно к рассматриваемой проблеме состоит в следующем.

1). Для каждой области существует разделяющая гиперповерхность h_i в n-мерном евклидовом пространстве Y. В аналитическом виде данная гиперповерхность представляет собой непрерывную функцию:

, , (6.7)

где – множество непрерывных функций, заданных на Y.

В дальнейшем (6.7) называется разделяющей функцией.

2). Разделяющая функция обеспечивает максимальную точность при распознавании текущих технических состояний, но является неизвестной. Поэтому следует выбрать аппроксимирующую функцию

, (6.8)

с помощью которой ищется приближение к разделяющей функции.

3). Мера отклонения аппроксимирующей функции (6.8) от аппроксимируемой (6.7) определяется как математическое ожидание случайной выпуклой функции от разности :

. (6.9)

4). Оптимальная аппроксимация соответствует получению такого вектора , при котором достигается минимум функционала (6.9):

. (6.10)

В выражении (6.10) указывается, что вектор отыскивается в n-мерном вещественном пространстве (которое, как известно является евклидовым). В дальнейшем множество, на котором производится поиск указанного вектора, будет конкретизировано.

5). Функционал (6.9) невозможно задать в явном виде, так как неизвестен ни закон распределения функции , ни ее числовые характеристики, в частности математическое ожидание. По этой причине искомый вектор может быть получен только на основе отдельных реализаций функционала (6.9) в процессе использования обучающих образов из выборки (6.5).

6). Процесс обучения обеспечивает получение изображений со статистически независимыми (некоррелированными) координатами в случае разложения аппроксимирующей функции с помощью ортогональной системы функций¹

(6.11)

в соответствии с выражением

. (6.12)

С учетом (6.11) и (6.12) функционал (6.9) принимает вид

. (6.13)

Далее система функций (6.11) называется G-преобразованием вектора Y.

Так как выражение функционала (6.13) неизвестно, для поиска его минимума используются измеренные градиенты реализаций функции . Иначе, минимум выражения (6.13) может быть найден решением градиентного уравнения

, (6.14)

где ;

;

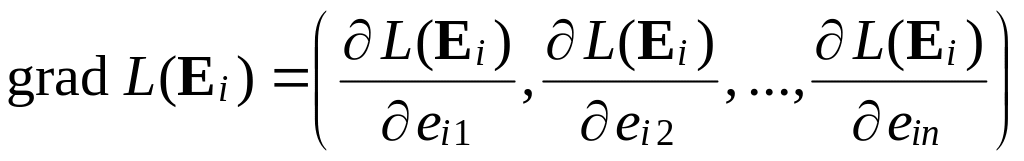 – частная производная по координате .

Если функционал (6.13) выпуклый (имеет единственный экстремум), корень уравнения (6.14) дает оптимальное значение вектора . Единственность экстремума функционала (6.13) имеет место, если использовать квадратичную меру отклонения аппроксимирующей функции от аппроксимируемой:

. (6.15)

Последнее утверждение очевидно, поскольку графически каждая реализация функции (6.15) представляет собой параболу.

В случае использования функции вида (6.15) минимум функционала (6.13) может быть найден с помощью алгоритма Роббинса-Монро [2]. Данный алгоритм представляется в виде рекуррентных соотношений

, , (6.16)

где ,  – последовательность, удовлетворяющая следующим требованиям:

.

Данные соотношения показывают, что последовательность должна быть сходящейся, сумма ее элементов является неограниченной, а сумма квадратов элементов – ограниченная величина.

Наиболее простым вариантом такой последовательности является гармонический ряд

, (6.17)

который и применяется в дальнейшем.

С учетом (6.17) рекуррентные соотношения (6.16) принимают вид

, , (6.18)

а для каждой координаты вектора E_i соотношения представляются как

, . (6.19)

Выражения (6.18) и (6.19) позволяют формировать изображение на последующем шаге через это же изображение на предыдущем шаге и очередной обучающий образ из выборки (6.5). Все алгебраические операции, которые предусмотрены в выражениях (6.18) и (6.19), определены аксиоматикой евклидовых пространств.

В качестве вектора начального приближения используется произвольный обучающий образ из выборки (6.5) после его G-преобразования:

. (6.20)

Выражение (6.20) реализует первый шаг обучающей процедуры, соотношения (6.18) применяются со второго шага. Поэтому в (6.17) и не указан первый элемент гармонического ряда – единица. Известно [7], что исключение из ряда любого конечного числа элементов на его сходимость или расходимость не оказывает никакого влияния. Следовательно, исключение единицы не влияет на свойства гармонического ряда.

Следует подчеркнуть, что на множестве всех G-преобразованных элементов пространства Y порождается новое евклидово пространство . В нем также выделяются частично пересекающиеся между собой области . Множество

построенных изображений содержится именно в данном пространстве: .