4.2.2. Основные свойства множества Парето

Так показатель f1=C желательно минимизировать, а показатель f2=Э максимизировать, то из рисунка 4.5 следует, что четвертый вариант ПО предпочтительнее второго варианта (последний имеет меньшую эффективность и в то же время большую стоимость). Таким образом, из шести представленных вариантов ПО лишь три (первый, четвертый и третий) могут претендовать на роль лучшего и являются недоминируемыми альтернативами. Обобщением рассматриваемого подхода к изображению множества Парето является подход, в котором наряду с двумя перечисленными критериальными функциями f1=C и f2=Э вводится еще одна критериальная функция f3=Т, где Т — время жизненного цикла соответствующей ПО. В этом случае график векторных оценок оказывается пространственным и изображается в наиболее наглядной плоской проекции или же представляется несколькими плоскими сечениями.

SPIIRAS

31

4.2.2. Основные свойства множества Парето

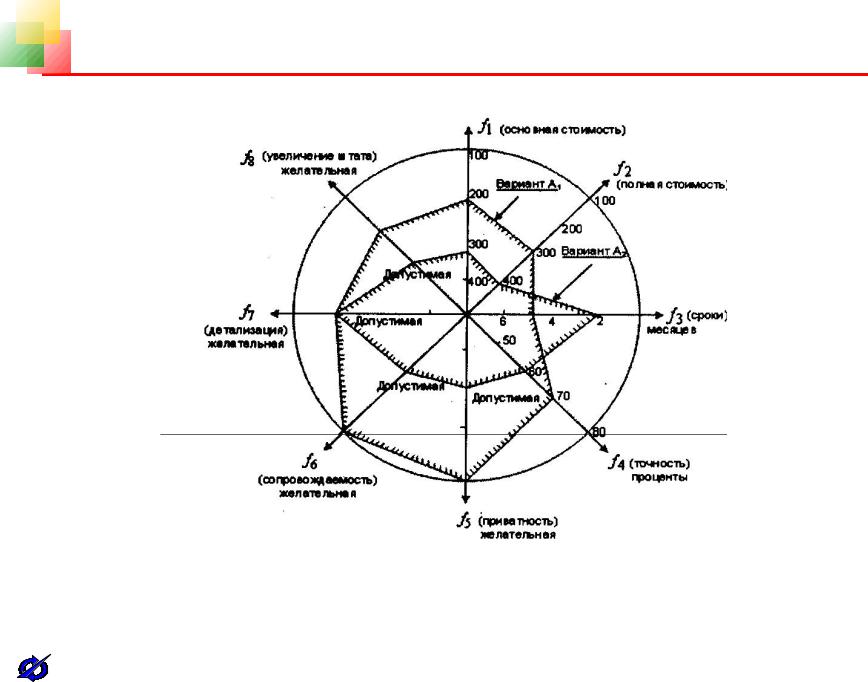
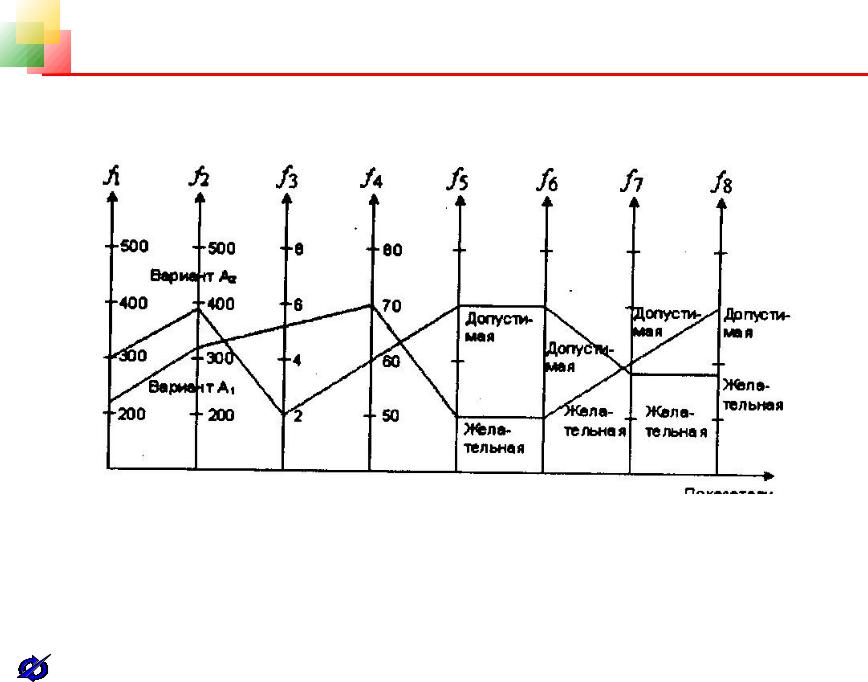
В том случае, если число критериальных функций больше трех, для графического представления пространства критериальных функций широко используют полярные и линейные диаграммы. На рисунках 4.6, 4.7 для примера проведено сравнение двух проектов создания программно-математического обеспечения АСУ (варианты А1 и А2) с использованием полярных диаграмм (диаграмм Кивиата) и линейных диаграмм. При этом рассматриваются восемь основных критериальных функции [1,16]: f1 — основная стоимость; f2 — полная стоимость; f3 — сроки создания; f4 — точность удовлетворения требований; f5 — приватность; f6 — сопровождаемость; f7 — детализация; f8 — показатель, характеризующий рост штата сотрудников. На радиальных лучах диаграммы откладываются как числовые значения соответствующих показателей (f1, f2, f3, f4), так качественные характеристики (градации, уровни): неприемлемый, приемлемый, промежуточный, желательный. В этом случае лучшей альтернативой является та, которой соответствует большая область круга, или та, которая по форме лучше приближается к окружности. Представление альтернатив с использование линейных диаграмм (рисунок 4.7) менее наглядно по сравнению с полярными диаграммами. Однако в этом случае построение соответствующих графиков проводить проще, а добавление новых критериальных функций не требует перестройки всего графика, как это приходится делать в случае полярных диаграмм.

SPIIRAS

32

4.2.2. Основные свойства множества Парето

Рис. 4.6.

SPIIRAS

33

4.2.2. Основные свойства множества Парето

Рис. 4.7.

SPIIRAS

34

4.2.3. Методы построения множества Парето

Приведенные в п.4.2.2 свойства множества Парето могут быть использованы для построения (исследования) данного множества (либо его подмножеств) или определения его характеристик в конкретных прикладных задачах. При этом

большинство методов определения указанного множества nd основано на

s

сформулированных условиях оптимальности. Чаще всего используются

необходимые условия оптимальности, состоящие в том, что если точка

x0 эффективна (в том или ином смысле), то она является решением задачи максимизации или минимизации (возможно, при некоторых дополнительных ограничениях) числовой функции специального вида при надлежащим образом назначенных величинах параметров, входящих в эту функцию и (или) ограничения.

В этом случае задача выделения всех эффективных решений сводится к соответствующей скалярной параметрической задаче математического программирования. Указанную замену исходной задачи векторной оптимизации параметрическим семейством обычных экстремальных задач часто называют скаляризацией исходной задачи. Однако в этом случае получаемое множество может содержать «лишние» точки, которые не являются эффективными и

соответствующих скалярных параметрических задач, удовлетворяющие им, являются эффективными.

SPIIRAS

35

4.2.3. Методы построения множества Парето

К настоящему времени наиболее конструктивные результаты, связанные с построением множества Парето, получены для случаев, когда

оказываются справедливы свойства 4 и 5, которым должны удовлетворять все точки множества Парето. Алгоритм поиска указанных точек сводится к решению следующей совокупности экстремальных задач:

i

Последовательно перебирая значения i(i ), можно получать точки множества Парето. Геометрическая интерпретация данного процесса сводится к построению опорных гиперплоскостей к множеству допустимых значений критериальных функций .

SPIIRAS

36

4.2.3. Методы построения множества Парето

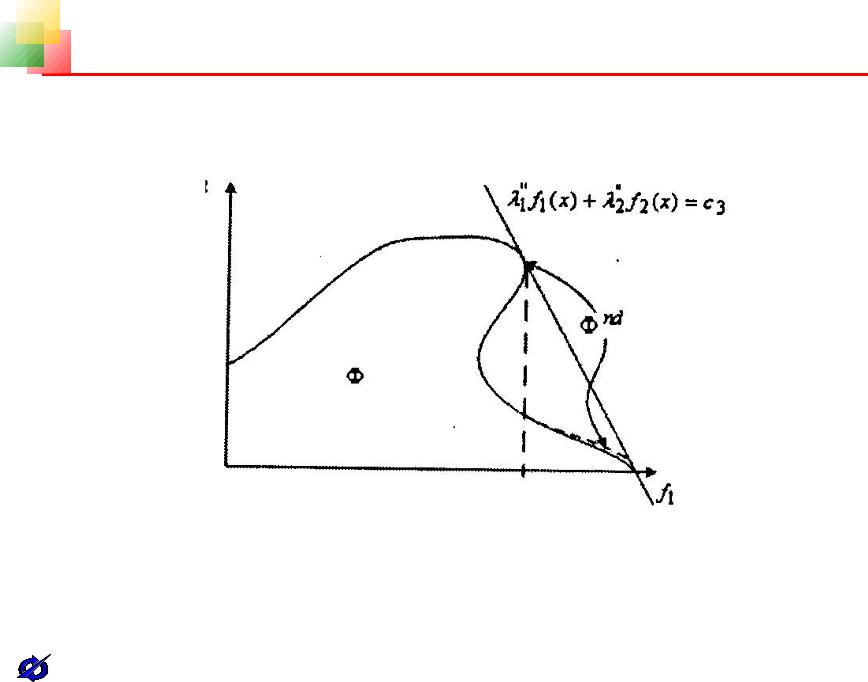
На рисунке 4.8 показан для случая двух критериальных функций пример построения двух линий уровня, которые касаются множества в точках, принадлежащих nd. Следует подчеркнуть, что требование выпуклости s и вогнутости fi существенно, т.к. если данные требования не выполняются, то решение задач (4.12) не гарантирует получение всех точек множества Парето. Это иллюстрируется геометрическим примером, представленным на рисунке 4.9. На данном рисунке точки множества nd, выделенные штриховой линией, не могут быть выделены ни при каких коэффициентах fi в задаче (4.12).

SPIIRAS

37

4.2.3. Методы построения множества Парето

Рис. 4.8.

SPIIRAS

38

4.2.3. Методы построения множества Парето

Рис. 4.9.

SPIIRAS

39

4.2.3. Методы построения множества Парето

Частным случаем постановки задачи (4.12) является задача многокритериального линейного программирования, в которой множество s ограничено выпуклой оболочкой, натянутой на конечное множество точек (вершин), называемой выпуклым многогранником [15, 24]. При этом все линейны. Вершины рассматриваемого выпуклого многогранника, образующие конечное множество V, и являются объектом первоначального исследования.

SPIIRAS

40