Zadanie_na_kursovuyu_i_laboratornye_raboty / Заочники весна 2019 / Блок / Блок

3. Основные свойства и показатели качества моделей и полимодельных комплексов

Подставим их в формулу (3.1):

u(1) = 0,5 · wт + 1 · wв u(2) = 0,6 · wт + 0,5 · wв.

Двумерные оценки полезности зависят от соотношения важности показателей. Если принять их равноценными wт = wв = 0,5, то предпочтение будет отдано стрелку 1 (см. столбец 4 табл. 3.1). Если нас интересует только результативностьстрельбы,топриwт = 1 и wв = 0 u(1)=0,5,аu(2)=0,6будет отдано предпочтение стрелку 2. Приравняв выражения u(1) и u(2), можно вычислить соотношение весов wт и wв, при котором предпочтение стрелку 2 по результативности стрельбы переходит на предпочтение стрелку 1 по качеству его действий.

Так называемую функциональную эффективность можно рассчитать через отношение целевых показателей к ресурсным. Для рассматриваемого примера численную оценку эффективности действий стрелков можно вычислить как Э(1) = 5/1 = 5 и Э(2) = 6/2 = 3. Из чего следует, что Э(1) > Э(2).

Экономическаяэффективностьопределяетсяисходяизбалансовыхуравнений – результаты должны быть обеспечены ресурсами. В нашем простейшем примере балансовые уравнения стрелков имеют вид:

стрелок 1: 5 · Ст = 1 · Св; стрелок 2: 6 · Ст = 2 · Св.

Положив стоимость одной минуты стрельбы в Св = 100 у. е., оценим стоимость точности стрельбы, Ст, стрелков:

Ст(1) = 100/5 = 20 у. е. и Ст(2) = 200/6 = 33,33 у. е. Поскольку Ст(2) > Ст(1),

точность стрелка 2 обходится дороже, чем точность стрелка 1. Следовательно, экономическая эффективность стрелка 1 выше.

Таким образом, по качеству, функциональной и экономической эффективности стрельбы предпочтение должно быть отдано стрелку 1, а по результативности стрельбы (без учета ее времени) – стрелку 2 (см. табл. 3.1). В зависимости от соотношения весов оценка по качеству может быть и противоположной. Различие анализируемых понятий как по формулам их оценивания, так и по результатам расчетов очевидно. В противном случае соответствующие термины избыточны.

Важно отметить, что для вычисления качества и эффективности используются одни и те же первичные показатели, характеризующие свойства системы. Но роль их в оценивании качества и эффективности различна. При оцениваниикачествамаксимизируютсяпоказателиназначенияобъектаиминимизируются ресурсные показатели, в то время как расчетный показатель эффективности устанавливает меру отношения между ними. Предназначение показателя эффективности состоит в том, что с его помощью производится расчет цены, которую приходится платить за получаемый полезный эффект (результат). В этом смысле предшественником показателя эффективности можно считать коэффициент полезного действия, отражающий долю полезно используемой энергии. Показатель эффективности можно рассматривать как обобщение КПД по отношению к любым видам потребляемых ресурсов (пространство, время, информация, материалы, люди и т. п.).

71

Квалиметрия моделей и полимодельных комплексов

Образно выражаясь, можно утверждать, что качество – это витрина продукта, а эффективность – прок от его использования. Для эффективности вводятся свои показатели и на их основе формулируются критерии. Важно выделить основную цель объекта в конкретной ситуации, что требует ее системного анализа.

Важность правильного выбора цели демонстрировалась в работе [10] на примере оснащения зенитными орудиями транспортных судов союзников во время Второй мировой войны. Они оказывались неэффективными с точки зрения затрат на нанесение ущерба атакующим самолетам противника и эффективными в отношении защиты судов.

Приведенный пример относится к классической проблеме отделения «мух от котлет». В любом военном противостоянии каждый стремится и защититьсебяинанестиущербпротивнику.Чтоважнее?Вданномпримере важнее сохранить груз и транспортирующий его корабль, а ущерб, наносимый зенитками самолетам врага, вторичен. Обоснованием этому является то, что стоимость корабля и груза несопоставима со стоимостью зенитных орудий, и то, что транспортное судно не является атакующим средством.

Пассивным способом защиты от поражения противником является маневренность объекта, понимаемая как уход от поражения. Меры, принятые для сохранения объекта (О), эффективны, если маневренность объекта поражения превышает маневренность средства поражения (СП). Это условие формулируется как: Время маневра (О) < Время маневра (СП).

Эффективность защиты объекта по маневренности будет определяться затратами на обеспечение лучшей маневренности относительно общей стоимости объекта.

В силу того что маневренность транспортного судна заведомо хуже маневренности нападающего на него самолета, сохранность судна следует обеспечивать активными средствами защиты. Здесь эффективность защиты от поражения должна рассматриваться через соотношение затрат на зенитки и стоимости судна с грузом. Затраты на установку и использование зениток определяются исходя из назначенного сектора поражения самолетов, их максимального числа, интенсивности и точности стрельбы зениток. Они рассчитываются при решении соответствующей оптимизационной задачи.

Рассмотренный пример показывает ситуативность показателя эффективности объекта и необходимость выполнения системного анализа для его нахождения и вычисления количественной оценки. В тех случаях, когда известна статистикаисследуемого явления, имеетсявозможность вычисления среднего выигрыша (или потерь) от использования ресурсов, предназначенных для достижения поставленной цели.

3.3.Показатели адекватности моделей

иполимодельных комплексов

Адекватность модели или ПМК как соответствие моделируемым свойствам объекта может быть определена только при наличии данных об этих свойствах объекта и возможности их моделирования. Но эти условия не

72

3. Основные свойства и показатели качества моделей и полимодельных комплексов

всегда выполнимы. Примером отсутствия объективных данных для моделирования являются редкие явления природы (например, падение метеорита), а примером невозможности проведения физического эксперимента, моделирующего событие, могут быть неприемлемые затраты ресурсов или неприемлемый ущерб для личности (например, при испытании лекарств) или окружающей среды (моделирование аварий, катастроф, военных действий). Отсутствие объективных данных о моделируемом объекте означает невозможность оценивания адекватности модели объекту. В связи с этим модели разделим на два класса: подлежащие и не подлежащие оцениванию адекватности объекту.

Свойство P, присущее объекту Ob и моделируемое моделью M, измерим значениями y Y: y(Ob) и y(M) соответствующего показателя. Мера близости j-го свойства модели yj(M) его значению yj(Ob) у объекта-оригинала оценивается разностью [11]:

Величина ε характеризует меру допустимого несоответствия j-го свойства модели j-му свойству объекта-оригинала. Оценивание адекватности модели по n моделируемым свойствам осуществляется путем сопоставления их векторных оценок y(M) = ( y1(M), …, yj(M), …, yn(M)) и y(Ob) = (y1(Ob), …, yj(Ob), …, yn(Ob)). При последовательном приближении модели к свойствам объекта-оригинала условие (3.2) служит правилом остановки отладки модели в случае его выполнения для всех j = 1¯,n̅. моделируемых свойств объекта Ob.

Аналитическая модель, представленная функцией n переменных, отражает n свойств объекта-оригинала. Одинаковый диапазон [0, 1], применяемый для измерения свойств модели, позволяет объединять их оценки в общую оценку качества модели независимо от субъективного или объективного способа оценивания этих свойств.

Поэлементное оценивание адекватности модели сложному объекту, характеризуемомумногимидесяткамипоказателей,представляетсобойсложную и не всегда выполнимую процедуру. Эта проблема может быть решена сопоставлением объекта и модели по одному – целостному свойству, отражающему конечный эффект применения объекта. Сопоставление модели объекту по целостному свойству можно выполнить через измерение расстояния ρ(M, Ob) между соответствующими точками в n-мерном пространстве элементарных свойств объекта. В качестве аргумента в соответствующих функционалахрассматриваютвеличинуразностивыходныхсостоянийобъекта y(Ob) и модели y(M). В этом случае условие адекватности (3.2) по n свойствам обобщается в условие:

В идеальной ситуации указанная мера близости ε объекта и модели должнаравнятьсянулю.Однаконапрактикевсилурядапричин(различные свойства объекта и модели, неопределенность исходных данных, измери-

73

Квалиметрия моделей и полимодельных комплексов

тельные и вычислительные погрешности и т. п.) вероятность (возможность) получения ε = 0 близка к нулю. Условие (3.3) будем называть ε-адекватно- стью. Для измерения расстояния ρ(M, Ob) могут использоваться различные метрики. Так, при детерминированном описании данных систем чаще всего используются метрики Евклида, Чебышева, Хэмминга, Ли и др. [11].

Встохастическом случае могут быть предложены меры адекватности, основанные на количественномоценивании расстояний междуслучайными выборками (первая ситуация), полученными в ходе экспериментов над объектом Ob и моделью M, и расстояниями между статистическими законами, построенными по этим выборкам (вторая ситуация). Примеры задания метрик для детерминированного случая приведены в табл. 3.2, а для стохастического случая – в табл. 3.3.

Втаблицах приняты следующие условные обозначения:

ȳ, ȳ(0), σ2y, σ2y(0) – статистические математические ожидания и дисперсии случайных величин ŷ(t), ŷ(0)(t), t T; λ, λ(0) – статистические оценки интенсивности обслуживания; m, n – количество элементов в соответствующих выборках. В общем случае y(t) Y(op), y(t) Y являются выборками N-мерных нормально распределенных генеральных совокупностей [12]. Обозначим через Ῡ и Ῡ<N>статистические математические ожидания векторных случайных величин Ŷ и Ŷ <N>соответственно. В случае равенства Ῡ = Ῡ <N> метрики ρ1 и ρ2 теряют смысл.

Табл. 3.2. Примеры задания метрик для первой ситуации.

2 Существуют непрерывные функции распределения Fȳ(y) и Fȳ(0)(y) в пространстве [0, 1]

3Существуют непрерывные функции распределения Fȳ(y) и

Fȳ(0)(y) в пространстве M[0, 1]

74

3. Основные свойства и показатели качества моделей и полимодельных комплексов

яния ρ̂ Ob( , M) в этом случае должна быть «сконцентрирована» в районе началакоординат.Дляпроверкиадекватностимоделиобъектупосоотношениям (3.4) и (3.5) необходимо задаваться величинами ε и δ, найти функцию или плотность распределения расстояния ρ̂Ob(, M), вычислить вероятность P1, P2 и сравнить ее с величиной (1 – δ). При сравнении статистических законов распределения выходных векторов yOb(t) и yM(t) расстояния между законамираспределениямогутбытьзаданыввидепредставленныхвтаблице 3.3 формул.

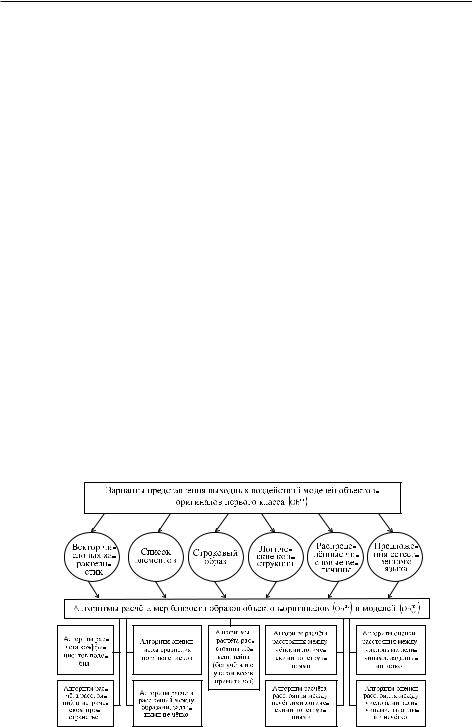
Для рассматриваемых ситуаций проверка адекватности модели M сводится к проверке статистической гипотезы о свойствах генеральных совокупностей выходных векторов yOb(t) и yM(t) при известных входных векторах xOb(t) и xM(t). На практике наряду с мерой близости, рассчитываемой по формуле (3.3), используется (в зависимости от способа описания модели) ряд других мер близости модели M и объекта оригинала. На рис. 3.3 приведены возможные меры близости объектов-оригиналов и различных представлений моделей, их описывающих, а также перечень алгоритмов, используемых для расчета указанных мер близости [12, 13].

Рис. 3.3. Классификация вариантов выходных воздействий моделей и алгоритмов расчета мер близости объектов-оригиналов и моделей.

75

Квалиметрия моделей и полимодельных комплексов

Количественная оценка адекватности моделей второго класса по изложенным в начале подраздела причинам затруднена, а то и просто невозможна. Кроме того, для соответствующих объектов моделирования само понятие «адекватность модели» требует уточнения. В этом случае целесообразно говорить уже (как уже отмечалось в подразделе 3.1) о полезности, пригодности модели для решения какого-то конкретного класса задач, связанных с объектом оригиналом. В работах [12, 13] приведены примеры оценивания полезности (адекватности) такого рода моделей.

3.4.Показатели сложности моделей

иполимодельных комплексов

3.4.1. Асимптотические оценки сложности

Выполнение моделирования связано с потреблением ресурсов. При компьютерном моделировании основными видами ресурсов являются оперативная память и быстродействие процессора. Память требуется для размещения модели, алгоритмов манипулирования моделью, исходных и выходных данных и информации, получаемых в результате моделирования. Процессор используется для выполнения моделирования.

Сложность модели рассчитывается на каждом этапе ее разработки. Предварительное оценивание сложности выполняется на этапе разработки модели на концептуальном и алгоритмическом уровне описания (на уровне DH-модели [14]). Для предъявления требований к объему памяти и быстродействию процессора системы моделирования рассчитываются показатели:

сложность по памяти (размерность задачи) и вычислительная сложность

модели. Например, сложность по памяти в задачах на графах характеризуется числом n2 ячеек, требуемых для хранения элементов матрицы смежности графа размерностью n × n, причем эта величина не зависит от числа дуг графа (числа единиц в матрице).

Известно,чтометодрешениязадачиможетбытьреализовансприменением различных алгоритмов. Их качество оценивается вычислительной сложностью, под которой понимается максимальное число шагов, необходимых длярешениязадачи.Вычислительнаясложностьалгоритма–этонаибольшее число его шагов как функция от размерности задачи. Например, вычислительная сложность решения задачи на матрице размерности n описывается функцией f(n). Под шагом алгоритма понимается выполнениелюбой машиннойкоманды.Числошаговопределяетвремярешениязадачи.Отсюдадляоценивания алгоритмов применяется также термин временная сложность [15].

Поскольку получение точной оценки f(n) числа шагов алгоритма для общего случая может вызвать затруднения, трудоемкость вычислений можно оценивать либо для конкретной модели либо использовать асимптотические оценки: верхнюю или нижнюю.

Асимптотическая сложность алгоритма определяет рост числа его шаговсростомразмерностизадачи.Вкачествеасимптотическойоценкифункции f(n) принимается функция g(n), которая дает:

76

3.Основные свойства и показатели качества моделей и полимодельных комплексов

1)верхнюю оценку O(g(n)), такую, что f(n) ≤ c · g(n) для n ≥ N;

2)нижнюю оценку Ω(g(n)), такую, что f(n) ≥ c · g(n) для n ≥ N, где c и N – положительные константы.

Алгоритм называется полиномиальным, если g(n) – полиномиальная

функция ni, i = 1, 2, 3…. Алгоритм, для которого не существует такой оцен-

ки, называется неполиномиальным или экспоненциальным.

При более детальном рассмотрении модели различают следующие виды сложности: информационную, структурную, функциональную [16].

Представим множество констант C алгебраической системы как домен значений переменной D = N. Параметр N характеризует информационную сложность переменной. В порядке возрастания информационной сложности он делится на четыре категории: два значения, конечное число значений

(k), счетное (k∞) и бесконечное множество значений (∞).

Представим носитель A алгебраической системы конечным множеством X мощности X =m.Тогдапрямое(декартово)произведениеX × X × … × X = Xn упорядоченных наборов или n-ок (x1, x2, …, xn) задает n-арный универсум. При n = 2 универсум X × X представляется полным графом с петлями.

В n-местное отношение Rn Xn входят часть n-ок (в частном случае все n-ки) из n-местного декартового произведения (универсума) Xn. Важным частным случаем является бинарное отношение R2 = R, состоящее из p упорядоченных пар вида (xi, xj).

Бинарное отношение R представляется графом G, число связей p в котором и характеризует структурную сложность модели. Нуль-граф R = , в котором отсутствуют упорядоченные пары (дуги) между вершинами, имеет нулевуюструктурнуюсложностьp =0.Полныйграф,содержащийвсесвязи между вершинами («каждая соединена с каждой и с собой»), имеет максимальную структурную сложность 2-го порядка p = m ∙ m = m2.

Структурная сложность n-го порядка (n-местное отношение Rn) интерпретируется множеством путей длины n, соединяющих вершины графа. Таким образом, структурная сложность модели может быть охарактеризована вектором сctr = (m, p, pn). Если модель содержит l отношений, то структурная сложность характеризуется матрицей размерностью l × 3.

Пусть домен D значений переменной представляет области определения и значений функции f: D × ... × D → D. Тогда функциональная сложность модели определяется видом функции, ее арностью (числом аргументов) n и числом функций k в модели. Сложность алгебраической функции определяется максимальной степенью ее переменных smax.

Сложность неэлементарной функции определяется максимальной степенью smax члена ряда, в который разлагается эта функция в области сходимости. Точность аппроксимации функции определяется младшим членом ряда.

Поскольку компьютерная обработка выполняется в численном режиме, число smax всегда конечно. Следует только помнить, что число smax зависит от численного метода реализации функции и не может быть определено по ее виду. Это лишний раз показывает, что для компьютерного моделирования недостаточно представления модели в аналитической форме записи. Необходимо ее рассматривать вместе с методом реализации модели. Тогда, имея

77

Квалиметрия моделей и полимодельных комплексов

численныехарактеристикиотношенийифункций,существуетвозможность численно оценить сложность модели в совокупности с реализующим ее методом. Раздельно сложность модели и метода оцениваются соответственно по объему используемой памяти компьютера и числу шагов алгоритма (вычислительная сложность). Таким образом, функциональная сложность модели характеризуется вектором сf = (smax, n), а сложность k-функциональной модели – матрицей размерностью k × 2.

Итак, при оценивании общей сложности аналитической модели следует учитывать следующие соображения. Каждая переменная отражает одно из элементарных свойств объекта-оригинала. Число значений характеризует точность представления этого свойства. Бинарное отношение характеризует структуру объекта, а n-арное отношение – взаимодействие его элементов. Функция одного аргумента отражает элементарную закономерность, выявленную в объекте-оригинале, а n-арная функция отражает n элемен-

тарных закономерностей.

С учетом сказанного выше общая сложность модели характеризуется

вектором с = (N, m, p, pn, smax, n). Это позволяет по векторным оценкам сложности моделей находить множество недоминируемых методов (множество

Парето). Однако при малом числе сопоставляемых методов и предложенных шести признаках велика вероятность того, что все будут принадлежать множеству Парето.

3.4.2. Показатели сложности иерархии моделей

Верхним уровнем любой иерархической модели является модель смыслов, ориентированная на человеческое восприятие. Ее называют онтологией предметной области. Формально она представляется семантической сетью – графом, помеченным знаками смыслов. Эта модель необходима для принятия решений человеком, но недостаточна для их автоматизации. Ее первичная конкретизация выполняется взвешиванием вершин и дуг графа. Примером может служить граф транспортной задачи.

Для отражения динамики в графовую модель вносится фактор времени. Примерами динамических графов являются граф переходов конечного автомата и вероятностная цепь Маркова. Дальнейшая конкретизация иерархической модели связана с раскрытием вершин графа моделями более высокого порядка.

Дляоцениваниясложностииерархиимоделейподходящимформализмом является модель с иерархической структурой сортов многосортной алгебраической системы. Переходу с одного уровня иерархии моделей на другой соответствует перевод языка одного сорта на язык другого со-

рта [16].

При переходе в иерархии сортов с нижнего уровня иерархии на верхний уровень применяется операция группировки, а при обратном переходе – операция свертки. Поясним это на следующих примерах. При переходе от скалярных оценок к векторной оценке используется операция группировки (конкатенации). При обратном переходе вектор свертывается в скаляр с помощью синтезирующей функции. При переходе от векторных оценок к

78

3. Основные свойства и показатели качества моделей и полимодельных комплексов

матричной оценке выполняется объединение векторов в матрицу. При умножении матрицы на вектор получаем вектор.

Таким образом, при оценивании двухуровневой иерархической модели к оценкам сложности модели каждого сорта должны добавляться функции перевода с языка одного сорта модели на другой, как прямые, так и обратные при двустороннем взаимодействии. Этой идее отвечает формула: сложность двухуровневой модели = сложность модели сорта 1 + сложность модели сорта 2 + сложность перевода (1, 2) + сложность перевода (2, 1).

Аналогичным образом оценивается сложность модели с большим числом сортов. При этом очень важно проверять каждый раз корректность перехода с одного уровня модели к другому.

3.4.3. Показатели сложности полимодельного комплекса

Сложность полимодельного комплекса следует рассматривать применительно к входящим в него моделям и связям между ними. Согласно концепции атома сложной системы [17], каждую модель примем за «черный ящик», опуская ее структурную сложность. Эта сложность учитывается только при раскрытии «черного ящика». А это означает оценивание только функциональной и информационной сложности моделей. Полная сложность полимодельного комплекса, помимо сложности входящих в него моделей, включает структурную составляющую. Структурная сложность должна характеризовать не только связи между моделями, но и их взаимодействие во времени.

Проблемы взаимодействия моделей как частей целого изложены в разделе 1 монографии. Сложность взаимодействия моделей будем рассматривать с точки зрения комбинаций значений на входах (входного алфавита)

модели M1.

Пусть модельM1 имеетn входныхпеременных,каждаяизкоторыхимеет mi значений. Тогда число комбинаций значений In на входах модели M1 определяется формулой:

Из общего числа входных комбинаций In моделью M1 отображаются на выходе модели только Inраб рабочих комбинаций Inраб In, а именно:

f: Inраб → Outраб. Очевидно, что на остальных In \ Inраб входных комбинациях значений выходные комбинации модели M1 не определены, что может

приводить к непредусмотренным выходным комбинациям. Они, в свою очередь, повлияют на модель M2, на входы которой поступает информация из модели M1. Описанная ситуация весьма характерна для систем, управляемых событиями.

Полная сложность полимодельного комплекса включает три составляющих:функциональнуюиинформационнуюсложностьвсехвходящихвнего моделейисложностьихвзаимодействия.Еслипредставитьполимодельный комплекс как автомат с памятью, то его сложность s можно выразить через

79

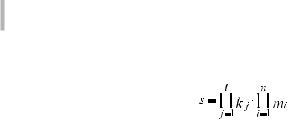
Квалиметрия моделей и полимодельных комплексов

произведение числа внутренних состояний отдельных моделей на число комбинаций значений на входах всего комплекса:

Здесь kj – число внутренних состояний j-й модели; l – число моделей в комплексе;

n – число входов полимодельного комплекса.

Очевидно, что не все состояния полимодельного комплекса являются рабочими, что и усложняет его отладку. Однако формула (3.7) позволяет дать ориентировочную оценку его информационной сложности.

В связи с употреблением расширенного понятиясостояние существует необходимость в его определении. В самом общем смысле (с учетом перехода на новые архитектуры вычислительных средств и концепцию инвариантности физическихивычислительныхпроцессов)подсостояниембудемпониматьсо-

вокупность наблюдаемых и вычисляемых параметров объекта в фиксирован-

ный момент времени. Под наблюдаемыми параметрами здесь понимается все то, что доступно восприятию субъекта. Наблюдаемыми (контролируемыми) могут быть как измеряемые, так и вычисляемые на их основе параметры.

Совокупность наблюдаемых параметров представима вектором их значений s(t) как функции от момента времени t. Если известна зависимость вектора s(t) от предыдущего вектора s(t – 1) и входного вектора x: s(t) = f(s(t

– 1), x), то она позволяет определить как предыдущие, так и последующие вектора системы. Примерами таких зависимостей являются дифференциальное уравнение и таблица переходов конечного автомата.

Однако такая зависимость отсутствует в хаотическом движении и нарушается в случае непредвиденного воздействия внутренних или внешних факторов. За примерами далеко ходить не надо. Ракета, будущая траектория полета которой известна, взрывается на старте или отклоняется от намеченного курса. Люди, поведение которых было вполне предсказуемо, внезапно погибают вследствие террористического акта. Эти примеры свидетельствуют в пользу того, что истинно только настоящее. Состояние s(t +1) может быть ожидаемым, но не неизбежным.

3.4.4. Зависимость сложности модели от способа описания

Зависимость сложности по памяти и вычислительной сложности от найденной закономерности наглядно демонстрируется на логико-комбинатор- ных задачах. Простейшим примером такой взаимозависимости является определение делимости целого числа на 4. При десятичном представлении числа необходимо выполнять деление n-разрядного десятичного числа поразрядно n10 раз. Сложность этого процесса пропорциональна числу разрядов O(n10). При двоичном представлении числа достаточно проанализировать два младших разряда на 0. Сложность этого процесса равна двум O(2). Налицо уменьшение сложности по памяти с n10 разрядов десятичного числа до двух младших разрядов двоичного эквивалента числа и вычислительной сложности с n10 до двух операций.

80