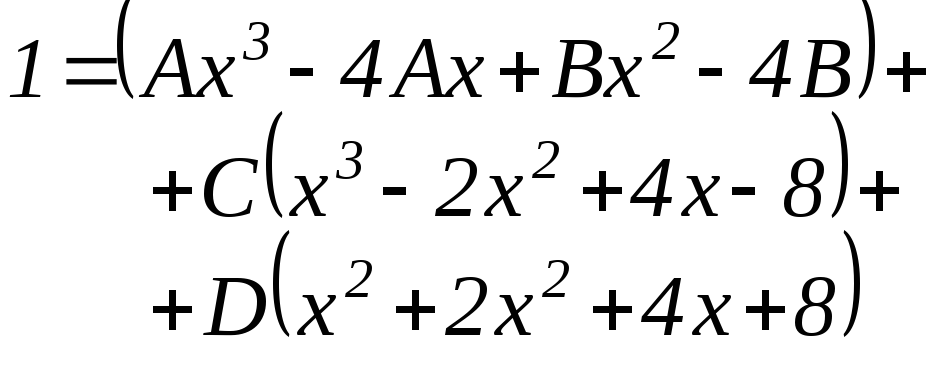Неправильная.

Правильная.

Выделить целую часть, т.е. представить дробь как сумму многочлена и правильной рациональной дроби.

1. Разложить знаменатель по корням, убедиться в несократимости дроби.

2. Представить как сумму элементарных дробей.

3. Определить постоянные коэффициенты элементарных дробей.

4. Проинтегрировать каждую элементарную дробь.



Рациональная дробь под знаком интеграла правильная, так как , .

Разложим знаменатель по корням:

, корни квадратного трехчлена .

Дробь несократима, так как числитель не обращается в ноль ни при одном из корней знаменателя (). Проверяется устно, например

.

Представим рациональную дробь как сумму элементарных дробей. В разложении только дроби типов (а) и (б), т.к. в знаменателе нет комплексных корней.

Приведем элементарные дроби к общему знаменателю и приравняем числители исходной дроби и суммы элементарных.

Для определения коэффициентов разложения сначала используем 1 способ. Подставим в равенство поочередно действительные корни знаменателя. Сразу получены три коэффициента.

Для определения В используем 2 способ. Требуется только одно уравнение, поэтому приравняем коэффициенты при наибольшей степени х : .

Представим в виде суммы интегралов и вычислим каждый.

Внесение под знак дифференциала

Используем свойства логарифмов.





Рациональная дробь под знаком интеграла правильная, так как , .

Знаменатель разложен по корням, причем имеет два действительных корня и два комплексно-сопряженных .

Дробь несократима, так как числитель не обращается в ноль ни при одном из корней знаменателя.

Представим рациональную дробь как сумму элементарных дробей. В разложении дроби типов (а), (б) и (в) т.к. в знаменателе есть комплексные корни.

Приведем элементарные дроби к общему знаменателю и приравняем числители исходной дроби и суммы элементарных дробей.

Для определения коэффициентов разложения сначала используем 1 способ. Подставим в равенство поочередно действительные корни знаменателя. Сразу получены два коэффициента.

Для определения В,С используем 2 способ. Требуются два уравнения, приравняем коэффициенты при наибольших степенях х: и . Для этого раскроем скобки в равенстве числителей.

=

Подставим найденные коэффициенты, представим в виде суммы интегралов.

Для второго интеграла: , для последнего .





Рациональная дробь под знаком интеграла правильная, так как , .Знаменатель разложен по корням, дробь несократимая.

Представим в виде суммы элементарных дробей.

Приведем элементарные дроби к общему знаменателю и приравняем числители исходной дроби и суммы элементарных дробей.

Подставим в равенство поочередно действительные корни знаменателя. Сразу получены два коэффициента.

Раскроем скобки в равенстве числителей, чтобы сравнить коэффициенты при одинаковых степенях х.

Требуются два уравнения, приравняем коэффициенты при наибольших степенях х: и .

Подставим найденные коэффициенты, представим в виде суммы интегралов.

