kornil / ФУБ семестр 2 / Высшая математика 2 семестр / ФУБ 2 семестр 2006 / c121_128

Тема 7. Теория

Тема 7. Определенные и несобственные интегралы

Определенный интеграл

Задача, приводящая к понятию определенного интеграла – задача о вычислении площади криволинейной трапеции.

Пусть на отрезке задана непрерывная функция , для определенности . Найдем площадь, ограниченную осью ОХ, прямыми и линией . Можно также говорить о площади под кривой или о площади криволинейной трапеции.

Для этого разобьем трапецию произвольным образом на частичные трапеции линиями, параллельными ОУ: , а затем заменим каждую прямоугольником со стороной и высотой , где - произвольно выбранная на частичном отрезке точка.

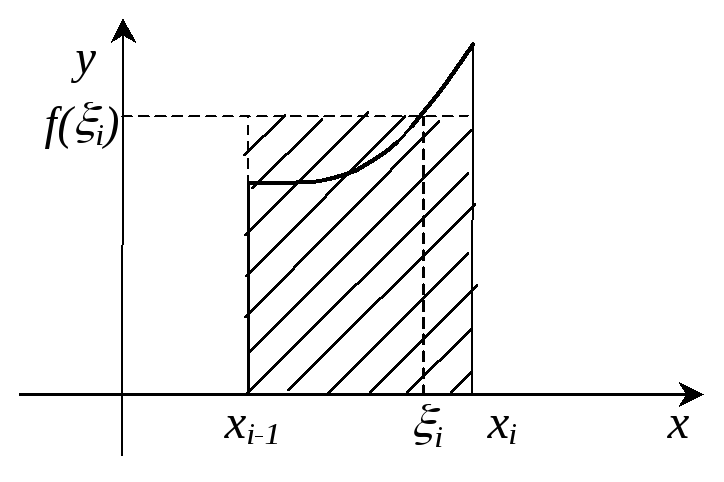
Составим сумму площадей всех прямоугольников, она будет приближенно равна площади всей криволинейной трапеции: . Такая сумма называется интегральной. Очевидно, будет тем более точно определять площадь криволинейной трапеции, чем на большее число частичных трапеций будет разбита исходная криволинейная трапеция. А при или, что то же самое, эти площади совпадут.

 Если существует конечный предел интегральной суммы , при , который не зависит от способа разбиения области на частичные отрезки и выбора точек , то он называется определенным интегралом функции на отрезке и обозначается

.

Здесь – нижний , – верхний пределы интегрирования.

 - Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия: если - представляет семейство функций, то -

- определенное число. 

 - Заметим, что не имеет значения, какой буквой обозначена переменная интегрирования, т.к. смена обозначений не влияет на интегральную сумму.

Свойства определенного интеграла.

1 - если поменять местами верхний и нижний пределы интегрирования, определенный интеграл поменяет знак.

2 - интеграл с одинаковыми пределами интегрирования равен нулю по определению.

3 ;

.

Аналогичные свойства есть и у неопределенного интеграла. Они показывают, что интегрирование – линейная операция и может быть распространена на любое конечное число слагаемых: .

4 Свойство аддитивности. Если - функция, интегрируемая на

и , где , то она интегрируема на и

Иными словами, отрезок интегрирования можно разделить на части какой-либо точкой и интеграл по всему отрезку заменить суммой интегралов по двум полученным отрезкам.

5 Свойство алгебраической площади. Определенный интеграл есть число того же знака, что и подынтегральная функция. То есть при вычислении площадей с помощью определенного интеграла можно получить отрицательную площадь.

 Теорема - о среднем значении функции на отрезке. Если непрерывна на отрезке (), то на этом отрезке существует хотя бы одна точка (), такая, что функция принимает в ней свое

среднее значение: .

Г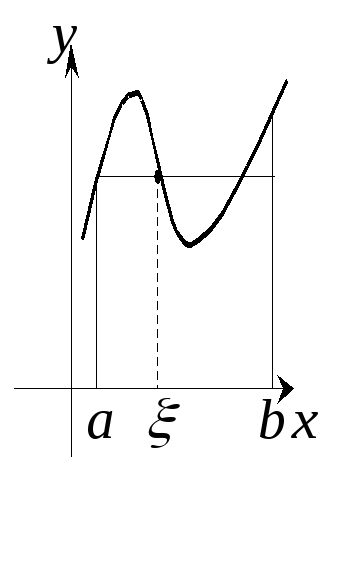 еометрический смысл теоремы: пусть , тогда существует по крайней мере одна точка , такая, что площадь криволинейной трапеции, ограниченной сверху непрерывной кривой будет равна площади прямоугольника с тем же основанием и высотой, равной : .

Вычисление определенных интегралов.

Формула Ньютона-Лейбница

Если для подынтегральной функции можно найти первообразную, то определенный интеграл можно вычислить по формуле Ньютона-Лейбница.

 - Формула Ньютона-Лейбница позволяет вычислить определенный интеграл как разность первообразных на верхнем и нижнем пределах интегрирования, не вычисляя предела интегральной суммы.

Можно выделить два этапа вычисления определенного интеграла.

• Одним из методов интегрирования (см. тему 6) находят первообразную.

• Вычисляют разность значений первообразной функции на верхнем и нижнем пределах интегрирования.

 - Сначала в первообразную подставляют верхний предел.

Особенности вычисления определенного интеграла

При замене переменных (подстановках)	При интегрировании по частям
Замена переменных, в отличие от неопределенного интеграла, предполагает не только замену подынтегрального выражения, но и замену пределов интегрирования.	Не следует забывать, что определенный интеграл – это число, при интегрировании по частям пределы интегрирования подставляют во все найденные функции.
; где новые пределы интегрирования находят как корни уравнений: ; .

Примеры вычисления определенных интегралов можно найти в разделе Примеры выполнения обязательных заданий по теме 7.

Вычисление площадей криволинейных фигур

Из задачи, рассмотренной в начале темы 7, приводящей к понятию определенного интеграла, ясно, что с его помощью можно вычислять площади плоских криволинейных фигур. При этом следует различать два случая.

Площадь заключена между заданными кривыми.	Площадь лежит под (над) заданными линиями (между линиями и осью ОХ).
Тогда, определив точки пересечения линий, т.е. пределы интегрирования, можно найти площадь как разность площадей под вышележащей и нижележащей кривой.	По рисунку видно, что в данном случае общая площадь складывается из площадей под линией и
; по свойству линейности

Среди геометрических приложений определенного интеграла можно еще отметить :	Вычисление длины дуги кривой от точки А до точки В :.
	Вычисление объемов тел вращения: , если вращение части дуги функции происходит относительно оси ОХ, , если вращение происходит относительно оси ОУ , .

126