Модуль5. Дифференциальные уравнения Практическое занятие № 1 Уравнения с разделяющимися переменными

Дифференциальное уравнение (5.1.2) называется уравнением с разделяющимися переменными, если его правая часть может быть представлена как произведение двух функций, каждая из которых зависит только от одной переменной:

. (5.1.1)

Уравнение (5.1.1) можно переписать в виде: . (5.1.2)

В последнем уравнении переменные разделены. Интегрируя его, найдем общий интеграл уравнения

.

Если существуют значения , при которых функцияобращается в нульто уравнение (10.1.2) будет иметь еще и решения

Задачи для аудиторного решения

Найти общий интеграл дифференциальных уравнений:

1) .2) .3) .

4) . 5) . 6)

Решить задачи Коши:

1),.2),;

Домашнее задание

1) ; 2) ; 3) .

Решить задачи Коши: 1) .2).

Практическое занятие № 2 Однородные дифференциальные уравнения

Дифференциальное уравнение называется однородным, если - является однородной функцией нулевой степени. Функция- называется однородной функцией нулевой степени, если выполняется тождество.

Если функция является однородной нулевой степени, то она удовлетворяет тождествуи ее всегда можно представить, как функцию отношения. Однородное уравнение можно представить в виде:.

С помощью замены переменной это уравнение сводится к уравнению с разделяющимися переменными: . Подставив эти выражения в уравнение, найдем.

Разделяя переменные и интегрируя, получим общий интеграл уравнения

.

При разделении переменных мы делим на , предполагая, что это выражение отлично от нуля. Если же существует такое значение, при котором, то мы имеем еще решениеили.

Уравнения вида: приводятся к однородному дифференциальному уравнению с помощью замены переменной. Решая систему уравнений: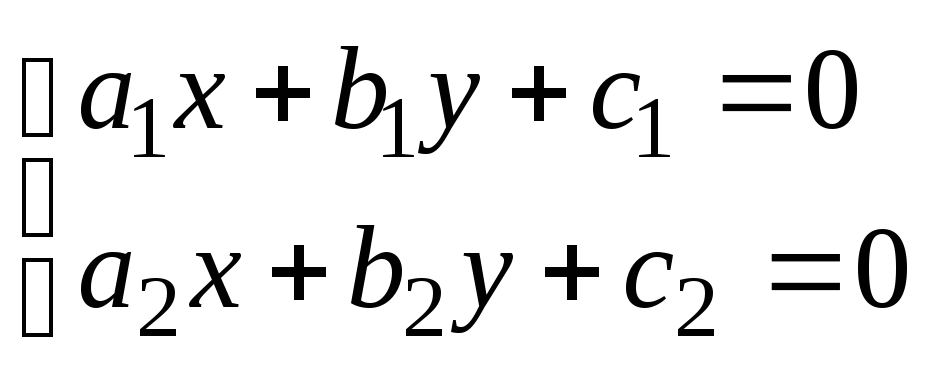найдем точку пересечения прямых.

Замена переменных приводит к уравнению

. Это однородное дифференциальное уравнение.

Изложенный метод нельзя применять, если прямые параллельны. Но в этом случае коэффициенты при текущих координатах пропорциональны и дифференциальное уравнение может быть записано в виде:

.

Следовательно, замена переменных преобразует уравнение в уравнение с разделяющимися переменными.

Задачи для аудиторного решения

Найти общий интеграл дифференциальных уравнений:

1) . 2) . 3) . 4) . 5) . 6) . 7)

Решить задачу Коши

Домашнее задание

1) ; 2) 3)

Решить задачи Коши 1) . 2)

Практические занятия №№ 3, 4. Линейные дифференциальные уравнения, Уравнение Бернулли

Дифференциальное уравнение называется линейным, если ивходят в него линейно, т.е. впервой степени: . Т.к., то уравнение приводится к виду:

(5.3.1)

где - правая часть линейного дифференциального уравнения.

Один из возможных способов решения уравнения (5.3.1) - способ Бернулли-Фурье. Будем искать решение в виде y=U(x)V(x). Таким образом, искомыми становятся функции U(x) и V(x).

Подставим y=UV и в (5.1.4), тогда

Найдем функцию V(x) как частное решение уравнения с разделяющимися переменными: . После интегрирования получим:, где постояннуюС можно задать произвольно.

Тогда функция U(x) также может быть найдена как решение уравнения с разделяющимися переменными .

Уравнение Бернулли сводится к линейному уравнению с помощью замены переменной. Разделим все уравнение на:и сделаем замену переменной. Тогда. Подставим в уравнение:или. Получили неоднородное линейное уравнение для функцииz. После его решения можно найти .