
Министерство образования и науки Российской Федерации
ГОУ ВО
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ОТЧЕТ
По лабораторной работе №5
На тему :«Численные методы поиска экстремума функций одной переменной. Методы дихотомии, «золотого сечения», Ньютона.»
Вариант 9
Отчет сдал ___Корнаухова_Д.А_____
Ст.гр_____БТПп-16-01________
Отчет принял______ _Юлдыбаев Л.Х.._____
Уфа 2017
Задание.
С точностью
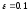 найти глобальный минимум функции одной
переменной
найти глобальный минимум функции одной
переменной
 методами дихотомии, «золотого сечения»
и Ньютона. Значения границ интервала
поиска
методами дихотомии, «золотого сечения»
и Ньютона. Значения границ интервала
поиска
 задать из условия унимодальности функции
в области глобального минимума (определить
визуально, нарисовав для этого график
функции).Сделать выводы о скорости
сходимости рассмотренных методов
минимизации функции.
задать из условия унимодальности функции
в области глобального минимума (определить
визуально, нарисовав для этого график
функции).Сделать выводы о скорости
сходимости рассмотренных методов
минимизации функции.
Решение.
График функции
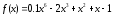 имеет вид:
имеет вид:
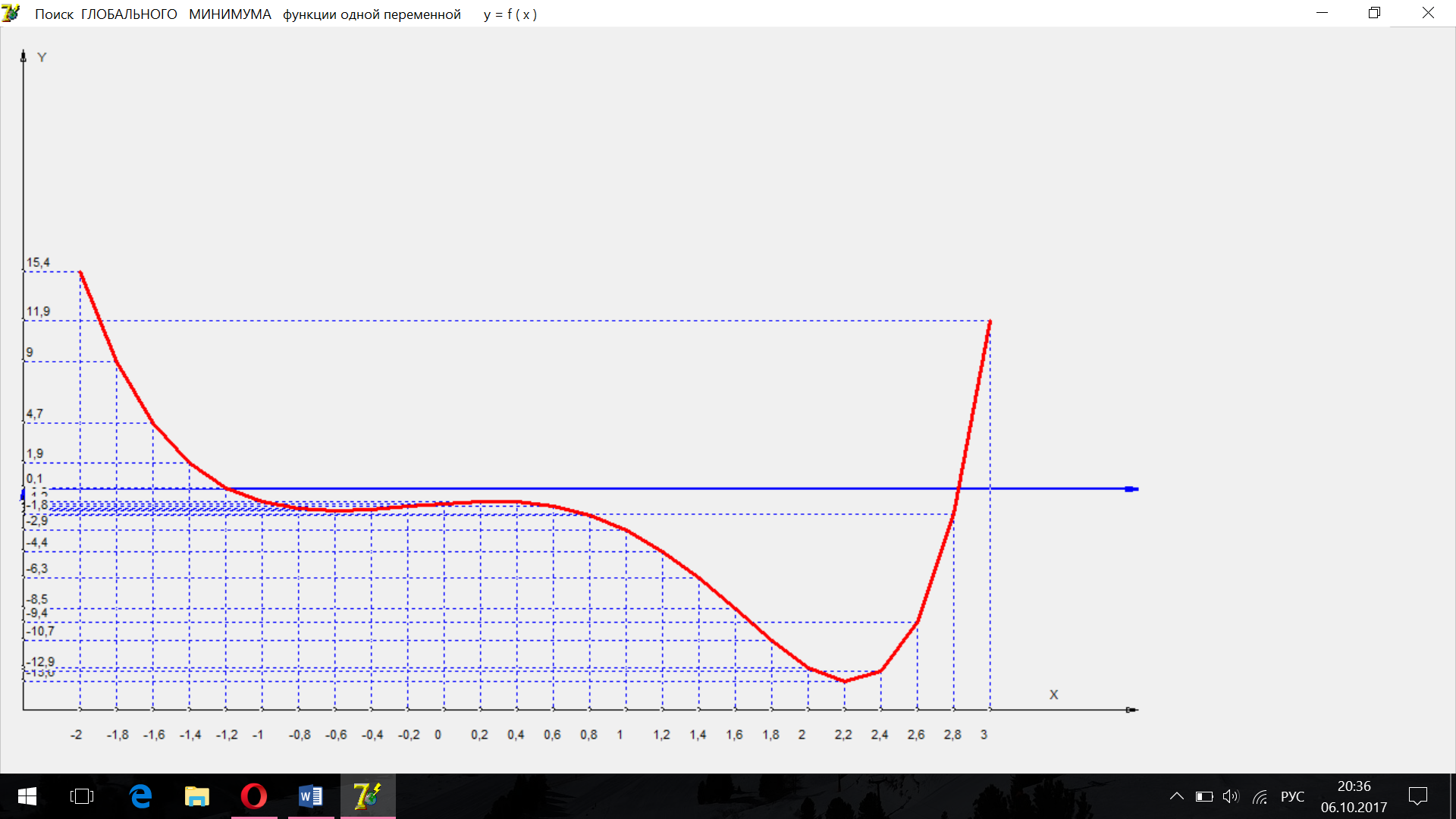
5.1 Поиск минимума методом дихотомии
1)
Первые два приближения возьмем на
расстоянии
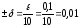 от середины выбранного отрезка
от середины выбранного отрезка
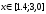 :
:
 ;
;
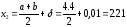 .
.
Так
как
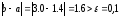 ,
то нужно выполнить следующее приближение.
,
то нужно выполнить следующее приближение.
Значения функции в этих точках
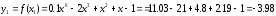 ;
;
Так
как
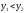 ,
то правый отрезок
,
то правый отрезок
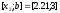 отбрасываем, т.е. считаем, что минимум
функции находится на отрезке
отбрасываем, т.е. считаем, что минимум
функции находится на отрезке
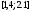 .
.
Итак,
перед второй итерацией считаем, что
 .
.
2)
Вторые два приближения возьмем на
расстоянии
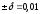 от середины отрезка
от середины отрезка
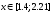 :
:
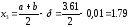
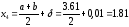 .
.
Так
как
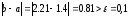 ,
то нужно выполнить следующее приближение.
,
то нужно выполнить следующее приближение.
Значения функции в этих точках

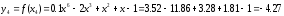
Так
как
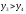 ,
то левый отрезок
,
то левый отрезок
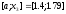 отбрасываем, т.е. считаем, что минимум
функции находится на отрезке
отбрасываем, т.е. считаем, что минимум
функции находится на отрезке
 .
.
Итак,
перед третьей итерацией считаем, что
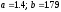 .
.
3)
Третьи два приближения возьмем на
расстоянии
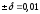 от середины отрезка
от середины отрезка
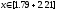 :
:
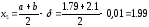 ;
;
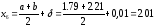 .
.
Так
как
 ,
то нужно выполнить следующее приближение.
,
то нужно выполнить следующее приближение.
Значения функции в этих точках
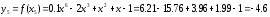
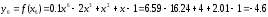
Итак,
 ;
число приближений
;
число приближений
 .
.
Ниже приведены расчеты нахождения минимума функции методом дихотомии, выполненные с помощью компьютерной программы.


5.2 Поиск минимума методом «золотого сечения»
1) Находим первые два приближения по формулам:
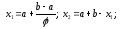 ,
где
,
где
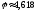 -
пропорция «золотого сечения».
-
пропорция «золотого сечения».
Для
отрезка
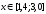 имеем
имеем

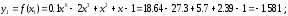
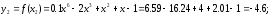
Так
как
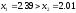 и
и
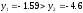 ,
то правый отрезок
,
то правый отрезок
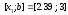 отбрасываем и считаем, что
отбрасываем и считаем, что
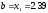 ,
а
,
а
 не меняется.
не меняется.
Так
как
 ,
то нужно выполнить следующее приближение.
,
то нужно выполнить следующее приближение.
2)
Теперь по правилу «золотого сечения»
делим отрезок
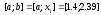 ,
причем точка
,
причем точка
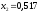 уже находится внутри этого отрезка, а
точку
уже находится внутри этого отрезка, а
точку
 ищем
как точку, симметричную точке
ищем
как точку, симметричную точке
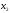 относительно середины отрезка
относительно середины отрезка
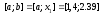 ,
т.е. по формуле
,
т.е. по формуле
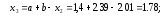
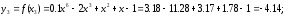
Так
как
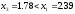 ,
а
,
а
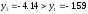 ,
то левый отрезок
,
то левый отрезок
 отбрасываем и считаем, что
отбрасываем и считаем, что
 ,
а
,
а
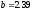 не меняется.
не меняется.
Так
как
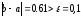 ,
то нужно выполнить следующее приближение.
,
то нужно выполнить следующее приближение.
3)
Теперь по правилу «золотого сечения»
делим отрезок
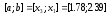 ,
причем точка
,
причем точка
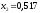 уже находится внутри этого отрезка, а
точку
уже находится внутри этого отрезка, а
точку
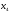 ищем
как точку, симметричную точке
ищем
как точку, симметричную точке
 относительно середины отрезка
относительно середины отрезка
 ,
т.е. по формуле
,
т.е. по формуле
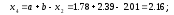

Итак,
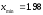 ;
число приближений
;
число приближений
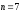 .
.
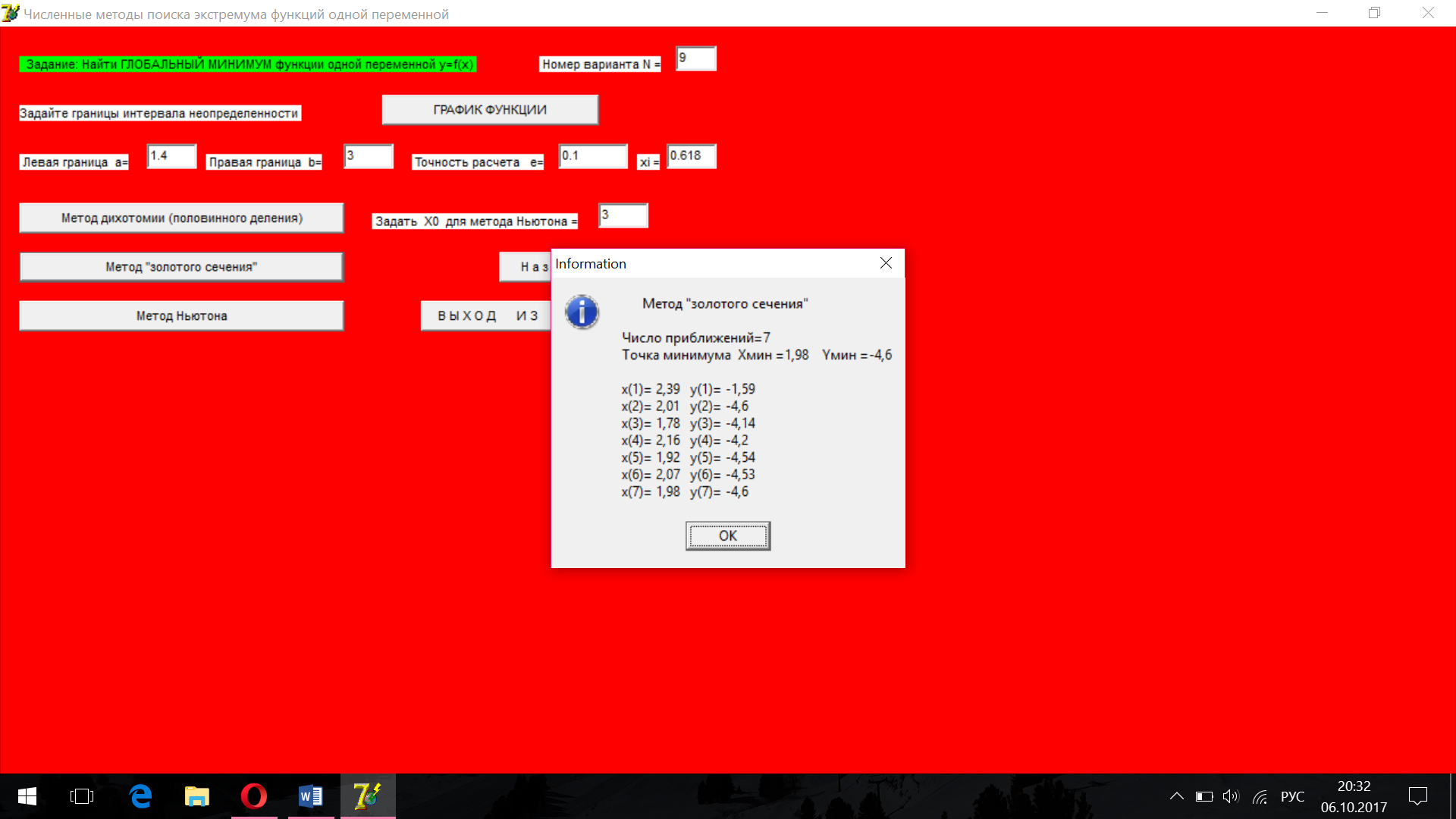
Ниже приведены расчеты нахождения минимума функции методом «золотого сечения», выполненные с помощью компьютерной программы.

5.3 Поиск минимума методом Ньютона
Для
метода Ньютона нужно задать начальное
приближение
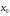 из условия
из условия
 , иначе процесс
сходимости не гарантирован.
, иначе процесс
сходимости не гарантирован.
Если
 ,
то
,
то
 и
и
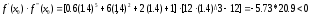 .
.
Если
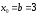 ,
то
,
то
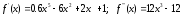 и
и
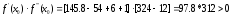 .
.
Следовательно,в
качестве начального приближения следует
выбрать
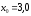 .
.
1) Находим первое приближение по формуле

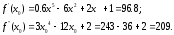
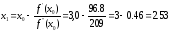
 ;
;
Так
как
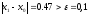 ,
то требуется второе приближение.
,
то требуется второе приближение.
2) Находим второе приближение по формуле
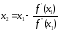
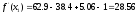


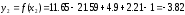
Так
как
 ,
то требуется третье приближение.
,
то требуется третье приближение.
3) Находим третье приближение по формуле

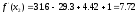
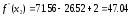

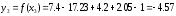
Итак,
 ;
число приближений
;
число приближений
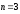 .
.
Ниже приведены расчеты нахождения минимума функции методом Ньютона, выполненные с помощью компьютерной программы.

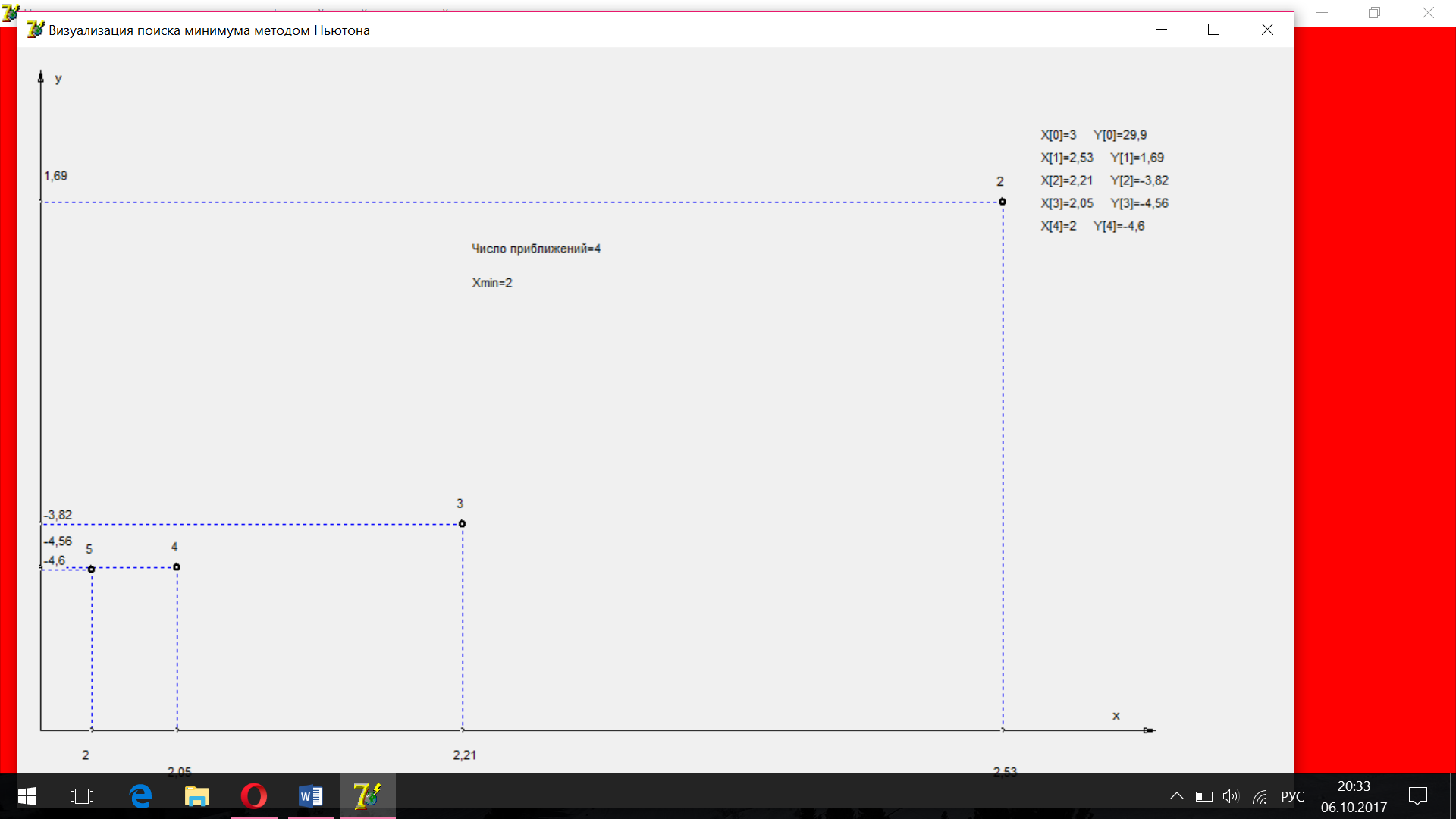
Результаты всех расчетов сведем в таблицу:
|
№ |
Название метода поиска |
Число приближений |
Точка минимума |
|
1 |
Метод дихотомии |
12 |
(1.98; -4.6) |
|
2 |
Метод «золотого сечения» |
7 |
(1.98; -4.6) |
|
3 |
Метод Ньютона |
4 |
(2; -4.6) |
Выводы:
При поиске минимума функции
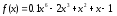 на отрезке
на отрезке
 самым быстрым оказался метод Ньютона
(4 приближения).
самым быстрым оказался метод Ньютона
(4 приближения).
