
- •Источники и потребители энергии в цепи (активные и пассивные двухполюсники). Баланс мощности.
- •Основные законы и уравнения цепей с сосредоточенными параметрами.
- •Цепи постоянного тока. Особенности.
- •Расчёт цепей постоянного тока (последовательное, параллельное, смешанное соединение, соединение «звезда» и «треугольник»)
- •Метод сворачивания
- •Метод уравнений Кирхгофа.
- •Метод узловых потенциалов
- •М етод контурных токов.
- •Метод эквивалентного генератора
- •Установившийся режим в цепи с последовательным соединением r, l и с
- •Установившийся режим в цепи с параллельным соединением r, l и с
- •Активная, реактивная и полная мощность Мгновенная мощность цепи синусоидального тока. Баланс мощности Мгновенная мощность – это произведение мгновенного значения напряжения и тока:
- •Эквивалентные параметры сложной цепи.
- •Основы комплексного метода расчета цепей синусоидального тока
М етод контурных токов.
В качестве искомых величин можно принять токи ветвей связи, или так называемые контурные токи. Знание контурных токов позволяет найти все реальные токи в схеме.
Уравнения
с контурными токами (контурные уравнения)
получают на основе второго
закона Кирхгофа;
их число равно числу независимых
уравнений, составленных для контуров,
т.е.
![]() .
.
Порядок решения.
Источники тока заменяются на эквивалентные источники ЭДС.
Произвольно задают положительные направления токов в ветвях.
Определяются независимые контура, в которые запускаются контурные токи, направление их выбирается произвольно.
Составляются контурные уравнения для независимых контуров и решая их находят контурные токи. NB: контурные токи могут получиться отрицательными.
Зная контурные токи, используя принцип наложения, находят токи во всех ветвях (с учетом знаков и направлений контурных токов). NB: Если ток получился отрицательным, необходимо изменить ранее выбранное направление на противоположное.
Проверку осуществляют по I закону Кирхгофа.
Пример.
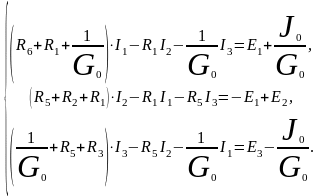
В скобках – собственное сопротивление контура; остальные – общие сопротивления.
Правило знаков правой части: если направление контурного тока совпадает с направлением источника записывают их со знаком «+», в противном случае – со знаком «-».
Метод эквивалентного генератора


Установившийся режим в цепи с последовательным соединением r, l и с
П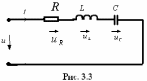 усть
усть
 ,
искомый ток можно представить в виде
,
искомый ток можно представить в виде
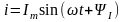 .
Значение имеет фазовой угол между током
и напряжением, то есть
.
Значение имеет фазовой угол между током
и напряжением, то есть
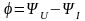 .
Можно положить
.
Можно положить
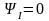 .
Тогда
.
Тогда
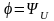 и задача ставится так: действует
напряжение
,
необходимо найти ток
,
то есть
и задача ставится так: действует
напряжение
,
необходимо найти ток
,
то есть
 ,
,
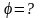 (рис. 3.4).
(рис. 3.4).
Запишем уравнение по второму закону Кирхгофа:
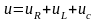 ,
или
,
или
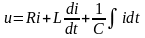 ,
или
,
или

 .
Это уравнение справедливо при любом
.
Это уравнение справедливо при любом
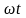 .
.
 ,
,
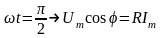 .
.
Отсюда
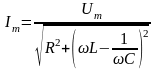 ;
;
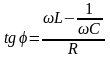 .
.
Здесь
 –
активное сопротивление ( этот параметр
характеризует необратимые процессы
преобразования электрической энергии
в тепло).
–
активное сопротивление ( этот параметр
характеризует необратимые процессы
преобразования электрической энергии
в тепло).
 –
индуктивное сопротивление (этот параметр
характеризует синусоидальное изменение
магнитного поля, сцепленного с цепью).
–
индуктивное сопротивление (этот параметр
характеризует синусоидальное изменение
магнитного поля, сцепленного с цепью).
 –
емкостное сопротивление (этот параметр
характеризует синусоидальное изменение
электрического поля в цепи).
–
емкостное сопротивление (этот параметр
характеризует синусоидальное изменение
электрического поля в цепи).
 –
реактивное сопротивление.
–
реактивное сопротивление.
 –
полное сопротивление. Таким образом,
имеем
–
полное сопротивление. Таким образом,
имеем
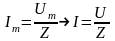 ,
,
 .
.
Построим векторную диаграмму. Для этого перепишем
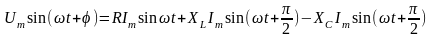 .
.
Начертим треугольник напряжений (рис. 3.5). Из него видно:
 1)
в активном сопротивлении ток и напряжение
совпадают по фазе;
1)
в активном сопротивлении ток и напряжение
совпадают по фазе;
2)
в индуктивности ток отстает от напряжения
на угол
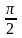 ;
;
3 )
в емкости ток опережает напряжение на
угол
.
)
в емкости ток опережает напряжение на
угол
.
Разделив все стороны треугольника напряжений на , получим треугольник сопротивлений (рис 3.6).
Установившийся режим в цепи с параллельным соединением r, l и с
П усть
усть
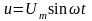 ,
,
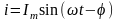 .
.
,
П о
первому закону Кирхгофа
о
первому закону Кирхгофа
 ,
,
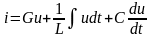 или
или
 .
(3.2)
.
(3.2)
Это выражение справедливо при любом .
Рассмотрим следующие случаи:
![]() ,
,
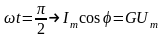 .
.
Отсюда
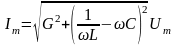 ,
,
 .
.
Здесь
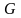 –
активная проводимость,
–
активная проводимость,
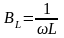 –
индуктивная проводимость,
–
индуктивная проводимость,
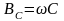 –
емкостная проводимость,
–
емкостная проводимость,
 –
реактивная проводимость,
–
реактивная проводимость,
![]()
 – полная
проводимость.
– полная
проводимость.
Таким
образом
 ,
,
 .
.
Построим векторную диаграмму (рис. 3.8). Для этого перепишем (3.2)
 .
.
Получили
треугольник токов. Поделив стороны
этого треугольника на
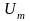 ,
получим треугольник проводимостей
(рис. 3.9).
,
получим треугольник проводимостей
(рис. 3.9).
