
- •Введение
- •Использование преобразование Лапласа для исследования динамических систем
- •Раздел 1. Элементарные звенья систем управления
- •Понятие звена
- •Усилительное звено
- •1.3. Интегрирующее звено
- •1.4. Апериодическое звено
- •1.5. Колебательное звено
- •1.6. Дифференцирующее звено
- •1.7. Звено запаздывания
- •1.8. Частотные характеристики типовых звеньев
- •1.8.1. Частотные характеристики усилительного звена
- •1.8.2. Частотные характеристики интегрирующего звена
- •1.8.3. Частотные характеристики апериодического звена
- •1.8.4. Частотные характеристики колебательного звена
- •1.8.5. Частотные характеристики дифференцирующего звена
- •1.8.6. Частотные характеристики звена запаздывания
- •1.9. Характеристики элементарных звеньев в табличной форме
- •Раздел 2. Линейный анализ и синтез систем управления с использованием математической лаборатории matlab
- •2.1 Анализ и синтез динамической системы в пространстве состояний
- •2.2 Устойчивость систем 1го, 2го порядка и более высокий порядок
- •2.3 Инерционная динамическая система 2-го порядка
- •2.4 Синтез инерционных систем первого и второго порядка
- •2.4.1 Выбор коэффициента усиления в инерционной системе I порядка.
- •2.4.2 Выбор коэффициентов усиления и гибкой обратной связи для инерционной системы второго порядка.
- •2.4.3 Применение методов аналитического синтеза для структуризации систем управления.
- •2.5 Исследование устойчивости для систем порядка n
- •2.5.1 Корневой анализ системы порядка n
- •2.6 Метод синтеза системы управления по желаемому значению частот и коэффициентов относительного демпфирования форм движения изолированной системы
- •2.6.1 Требование к распределению частот и относительных коэффициентов демпфирования изолированных форм движения
- •2.6.2 Выбор коэффициентов усиления по заданным требованиям к собственным значениям, частотам и коэффициентам относительного демпфирования в замкнутой системе
- •2.6.3 Математическая модель в пространстве состояний
- •2.6.4 Анализ характеристик замкнутой системы управления
- •2.7 Аналитическое конструирование оптимального регулятора (акор)
- •3. Алгебраические критерии устойчивости Рауса и Гурвица.
- •4. Частотные критерии анализа устойчивости и синтеза систем уравнения
- •4.1 Метод частотного анализа устойчивости Михайлова
- •4.2 Критерий устойчивости Найквиста-Михайлова и запасы устойчивости по амплитуде и по фазе для систем с единичной отрицательной обратной связью
- •4.3 Выбор коэффициентов усиления к в прямой и обратной цепи по заданному запасу устойчивости.
- •4.4 Метод наращивания устойчивых контуров. Выбор коэффициентов усиления позиционно-дифференцирующего и позиционно-интегрально-дифференцирующего контроллера
- •4.5 Расчет позиционного интегрально-дифференцирующего контроллера(pid)
- •5. Синтез корректирующих звеньев в прямой цепи
- •5.1 Расчет параметров передаточной функции фильтра средних частот (фсч)
- •5.2 Расчет параметров фильтра низких частот (фнч)
- •5.3 Расчет параметров фильтра высоких частот (фвч)
- •6. Синтез корректирующего звена в цепи обратной связи.
- •Процедура улучшения решения за счёт выбора параметров во втором приближении.
- •Раздел 7. Аналитический обзор методов исследования устойчивости систем автоматического управления
- •7.1. Критерии устойчивости [1, 7, 11, 12].
- •7.2. Частотные критерии устойчивости [7, 8, 11].
- •7.3. Запас устойчивости систем [7].
- •7.4. Точность систем [8].
- •7.5. Качество систем [1, 2, 8, 12].
- •7.6. Случайные процессы в системах [8].
- •Литература
1.9. Характеристики элементарных звеньев в табличной форме
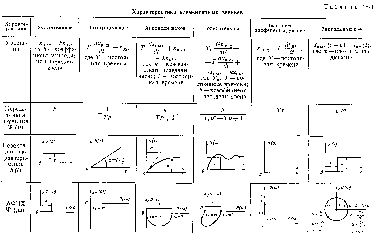
1
1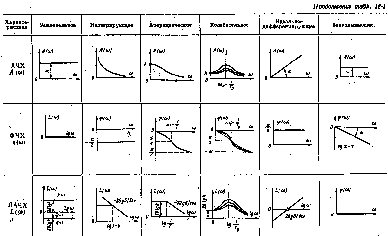
Раздел 2. Линейный анализ и синтез систем управления с использованием математической лаборатории matlab
Для разработки современных систем управления используются теории линейного анализа и синтеза. Для методов линейного анализа и синтеза разработана математическая лаборатория (MatLab), которая позволяет ввести исходные данные, указать решение требуемых задач и получить графические результаты расчетов.
Для нелинейных систем используются методы линеаризации и линейный анализ в области линеаризации.
Завершение исследований включает анализ нелинейности и дискретности цифрового управления на устойчивость, управляемость системы с нелинейными характеристиками приводов, измерителей и дискретности цифрового регулятора.
2.1 Анализ и синтез динамической системы в пространстве состояний
Рассмотрим дифференциальные уравнения движения в линейной стационарной системе:
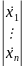 =
=
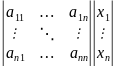 +
+
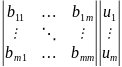 n
n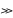 m
m
И алгебраические уравнения измерителя:
 =
=
 +
+
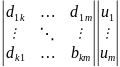
Эти уравнения записаны в матричной форме. Для исследования системы необходимо ввести элементы матрицы
В векторной форме:
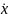 =
Ax
+ Bu
=
Ax
+ Bu
y = Cx + Du
Здесь А – матрица динамических коэффициентов;
В – матрица управления;
C и D – матрицы измерений
Исследование
устойчивости представляет собой анализ
собственного возмущенного движения в
случае равенства
нулю управления и начальным отклонении
координат:
u
= 0, x
(t=0)
=
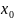
Понятие Ляпунова об устойчивости:
Если линейная система выведена из положения равновесия и затем совершает движение в Ɛ-окрестности положения равновесности (x = 0), то динамическая система устойчива.

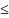 Ɛ
Ɛ
Динамическую систему называют асимптотически устойчивой, если предел ее движения заканчивается в положении равновесия.
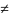 0
0
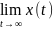 = 0
= 0
2.2 Устойчивость систем 1го, 2го порядка и более высокий порядок
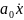 +
+
 x
= 0, u
= 0
x
= 0, u
= 0
Вводим
p
=
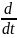 Оператор Лапласа
Оператор Лапласа
x(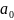 p
+
)
= 0,
0 – уравнение в операторной форме
p
+
)
= 0,
0 – уравнение в операторной форме
ap + = 0 – характеристическое уравнение
p*
= -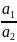 – вектор собственного значения
– вектор собственного значения
x
=

c – собственный вектор с =

Рис. Устойчивое и неустойчивое апериодическое движение
Для устойчивости линейной системы 1 порядка необходимо, чтобы ее вещественные корень был строго отрицательный. Если система описывается дифференциальным уравнением 1 порядка, то ее движение является апериодично устойчивым или неустойчивым.
Для устойчивости динамической системы необходимо существование сил или момента, которые будут направлены к положению равновесия при начальном отклонении.
Для асимптотической устойчивости необходимо существование демпфирующего момента, который будет всегда направлен против вектора линейной или угловой скорости.
Пример использования MatLab для определения устойчивости системы 1 порядка.
MatLab 6.5.1
Control
Toolbox
 линейный анализ и синтез
линейный анализ и синтез
Угловое вращение самолета по крену:
 =
=
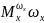
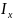 –
момент
инерции по крену;
–
момент
инерции по крену;
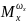 – коэффициент демпфирующего момента.
– коэффициент демпфирующего момента.
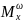 =
=

Для расчетов преобразуем в уравнение в форме Коши относительно производной
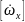 =
=

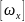
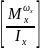 –элемент
динамических коэффициентов
–элемент
динамических коэффициентов
Для решения задачи указываем курсором на значок MatLab, загружаем систему и на наборном поле указываем исходные данные:
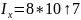
S = 180
L = 27
V = 200
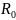 =
0.37
=
0.37
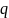 =
0.5 -
=
0.5 -
 V
V
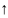 2
2
 =
-7.3
=
-7.3
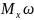 =
=
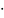 q
S
L
q
S
L
 =
=
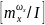
damp (A)
Собственное значение -3.5, коэффициент относительного демпфирования 1, собственная частота 3,5.
