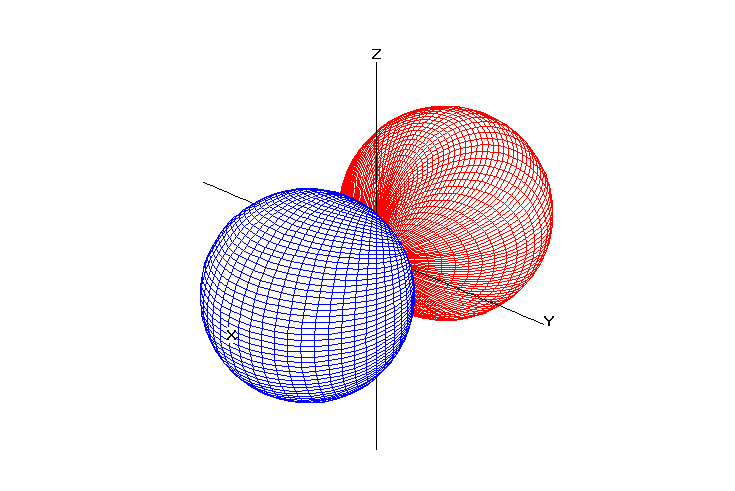Волновое уравнение для свободного электрона

Уравнение Шредингера легко решается в очень небольшом числе случаев. Самая простая задача – решение волнового уравнения для свободного электрона. Если на частицу, движущуюся вдоль оси х нет действия внешних полей, слагаемое потенциальной энергии в гамильтониане равно нулю, V = 0, а полная энергия равняется кинетической. Стационарное уравнение принимает вид:

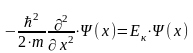
Уравнение имеет решения при собственных значения энергии 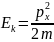, волновая функция свободного электрона . Предэкспонента А называется нормировочным множителем и вычисляется таким образом, чтобы интеграл плотности вероятности по всему пространству был равен единице.

Из полученных решений ясно, что энергия в отсутствии потенциальных полей имеет непрерывный спектр. А волновое движение представляет собой плоскую волну. Плотность вероятности, квадрат волновой функции, равный произведению комплексно сопряженных функций величина постоянная ψ²= А², т.е. вероятность обнаружить такой электрон в любой области пространства одинакова.

Электрон в одномерном потенциальном ящике

Потенциальный ящик представляет собой систему, ограничивающую движение электрона вертикальными стенками. Внутри ящика потенциальная энергия равна V= 0, а за бесконечно высокими стенками она бесконечно велика V= ∞. Электрон не может выбраться из этого ящика, и вынужден перемещаться внутри его (рис.13).

Рисунок 13. Одномерный потенциальный ящик

Уравнение Шредингера в этом случае совпадает с уравнением для свободной частицы. Однако на решение накладываются дополнительные ограничения, у стенок значение ψ-функции должны обратиться в ноль. Если ширина ящика равна a, граничные условия выглядят как: ψ(0)=0, ψ(а)=0. Электрон «мечется» между стенками, поочередно отражаясь от них, устанавливается стоячая волна, поэтому синусоида оказывается лучшим решением. С учетом граничных условий и нормировки решением является набор собственных энергий и соответствующих им волновых функций:

где n =1,2,3,4....

Параметр n называется квантовым числом. Решения отличаются друг от друга на целочисленные параметры, квантовая частица в потенциальном ящике имеет дискретный энергетический спектр. Плотность вероятности будет иметь явно выраженные максимумы, число которых зависит от квантового числа n (рис.14). Из рисунка видно, что, например, для n=2 вероятность обнаружить электрон в центре ящика равна нулю, а для n=1 или n=3 она максимальна.

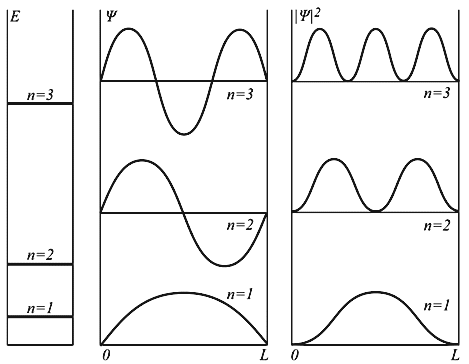
Рисунок 14. Поведение волновой функции и ее квадрата в одномерном потенциальном ящике в зависимости от квантового числа n.

Атом водорода

Атом водорода состоит из ядра и электрона, и уравнение Шредингера для него можно решить точно. Потенциальное поле, в котором движется электрон, имеет центральную симметрию (рис.15), поэтому уравнение следует переписать в сферических координатах (рис.16).

Рисунок 15. Атом водорода

Рисунок 16.Сферические координаты

Потенциальная энергия электрона представляет собой энергию кулоновского взаимодействия с атомным ядром. Заряд ядра и электрона по модулю совпадают, но имеют противоположный знак. Потенциальная энергия, которую нужно подставить в уравнение Шредингера:

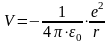
где ε₀ ≈ 8,85·10⁻¹² Ф/м  – электрическая постоянная.

Уравнение Шредингера принимает вид:

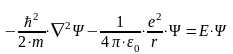
Решение существует:

а) при любых положительных значениях полной энергии. Это несвязанные состояния электрона, когда он улетает от ядра на бесконечность;

б) при отрицательных значениях энергии (E< 0), энергия имеет дискретный спектр.

Собственные значения Е, удовлетворяющие данному уравнению:

Целочисленный параметр n называется главным квантовым числом и номером энергетического уровня.

Решением уравнения Шредингера является набор волновых функций, отличающихся друг от друга величиной целочисленных параметров: n, l, m_l.

Параметры n, l, m_l носят название квантовых чисел: главное квантовое число n, орбитальное квантовое число l, магнитное квантовое число m_l.

Для первого энергетического уровня (n =1) значения lи m_l равны нулю. Это основное состояние атома водорода. Волновая функция основного состояния сферически симметрична и меняется только с расстоянием от ядра:

Радиальная зависимость плотности вероятности распределения электронов (электронной плотности) в основном состоянии атома водорода – это вероятность того, что электрон будет обнаружен в тонком сферическом слое радиуса r толщиной dr с центром в ядре. Вероятность, что электрон находится в слое равна dР= dVψ²=(4πr²ψ²dr). На рисунке 17 изображен график зависимости dp(r)/dr = 4πr²ψ².

Рисунок 17. Радиальная зависимость плотности вероятности распределения электронной плотности в основном состоянии атома водорода. Заштрихованная область соответствует электронной орбитали.

Кривая радиального распределения электронной плотности имеет максимум при r₀≈0,53Å. Этот наиболее вероятный радиус совпадает с радиусом первой боровской орбиты. Вероятность обнаружить электрон не обращается в ноль даже при бесконечном удалении от атома, однако, можно выделить область вблизи ядра, где она максимальна. Область пространства, в которой вероятность нахождения электрона 90% называется электронной орбиталью.

Волновые функции возбужденных состояний атома водорода могут не обладать сферической симметрией, тогда распределение электронной плотности будет зависеть от угловой координаты. Собственные функции оператора Гамильтона будут содержать квантовые числа l и m_l, связанные с угловым моментом количества движения электрона.

Физический смысл квантовых чисел

Энергия электрона определяется только  главным квантовым числом – n, которое может принимать целочисленные значения от нуля до бесконечности. Главное квантовое число совпадает с номером энергетического уровня.

Каждому собственному значению энергии  соответствует одна или несколько собственных функций  различающихся значениями квантовых чисел l, m_l.

Состояния с одинаковой энергией называются вырожденными, а число состояний с одинаковым значением энергии называется кратностью вырождения энергетического уровня.

Орбитальное квантовое числоlопределяет значение орбитального момента количества движения электрона L.

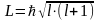
Возможные значения для орбитального числа находятся в интервале от нуля до (n –1). Квантовое число l характеризует энергетический подуровень. Традиционно подуровень со значением l = 0 обозначается буквой s, l = 1 – буквой p, l = 2 – буквой d, l = 3 – буквой f и т.д..

Орбитальное квантовое число определяет форму электронной орбитали.

М агнитное квантовое число m_l, определяет проекцию момента импульса во внешнем силовом поле на выбранное направление в пространстве, обычно ось z:

При заданном l магнитное квантовое число может принимать значения: -l, (-l+1),...,0,...,(l–1), l. табл.1.

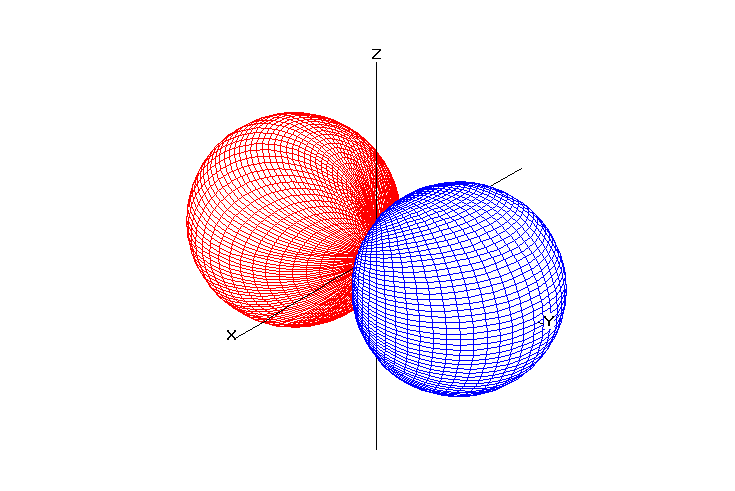
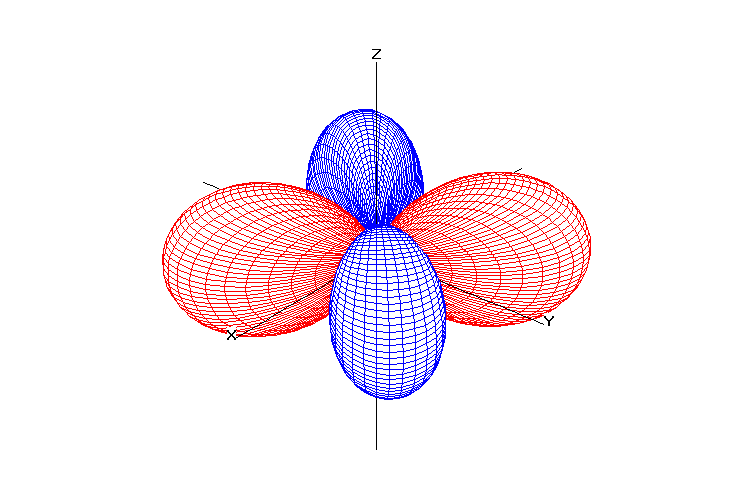
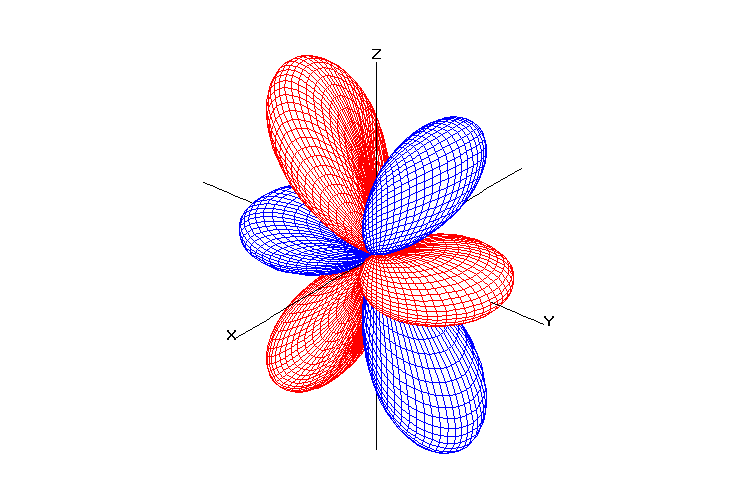
Таблица 1. Форма электронных орбиталей в зависимости от квантовых чисел l и m_l

	ml=-3	ml=-2	ml=-1	ml=0	ml=+1	ml=+2	ml=+3
l=0
l=1
l=2
l=3

Энергетические уровни атома водорода по Шредингеру совпадают с уровнями, полученными Нильсом Бором и коррелируют со спектрами испускания и поглощения. Однако, эксперименты отчетливо показывают расщепление линий атомных спектров в магнитном поле.

Для объяснения этих экспериментов в 1925 году физики Сэмюэл Гаудсмит и Джордж Уленбек ввели понятие спина. Они опубликовали смелую гипотезу о том, что электрон является носителем собственных механического и магнитного моментов, не связанных с движением электрона в пространстве. Первоначально многие физики предполагали, что спин обусловлен вращением электрона вокруг своей оси. Однако такая модель вращающегося «волчка» или заряженного шарика оказалась несостоятельной, так как расчет показал, что магнитный момент, равный по величине собственному магнитному моменту электрона можно индуцировать только при скорости вращения существенно превышающей скорость света. Кроме того, согласно современным представлениям, электрон – точечная частица, следовательно, у нее не может быть оси вращения.

Спин – это собственный момент количества движения элементарных частиц, имеющий квантовую природу, не связанный с перемещением частицы как целого. Спин электрона это внутреннее свойство электрона, такая же количественная характеристика квантовых частиц, как масса и заряд. Если заряд указывает на степень взаимодействия частицы с электромагнитным полем, то спин – с магнитным.

Спиновое квантовое число m_s характеризует проекцию спинового момента электрона на ось z и имеет два значения ±1/2.

Квантовое число m_s не вытекает из уравнения Шредингера. Теоретический вывод спинового числа следует из волнового уравнения Поля Дирака, учитывающего принципы специальной теории относительности.

Уравнение Шредингера можно решить для систем похожих на атом водорода – водородоподобных атомов. Такие атомы содержат ядро и только один электрон. Набор собственных энергий будет отличаться лишь на множитель равный заряду ядра.