2.2.4.Решение системы нормальных уравнений

Систему уравнений можно решить любым способом (подстановкой, методом Жордана-Гаусса и т. д.). Каждый из способов имеет свои достоинства и недостатки, заключающиеся либо в чрезмерной громоздкости, либо в потери точности вычислений. При использовании ЭВМ, когда громоздкость вычислений не играет заметной роли, систему можно решить методом «обратной матрицы». При расчёте «вручную» можно воспользоваться довольно простым, но не очень точным методом «исключения переменных». Разделим почленно каждое из уравнений на коэффициент при а_о.

Получим: a₀ + 6,96a₁ + 15,4a₂ = 224,2

a₀ + 8,16a₁ + 13,14a₂ = 222,35

a₀ + 5,9a₁ + 20,24a₂ = 248,86

Вычтем почленно из первого уравнения второе, а затем третье с целью полу­чения системы из двух уравнений с двумя неизвестными:

- 1,2a₁ + 2,26a₂ = 1,85 1,06a₁ - 4,84a₂ = - 24,66

Аналогично, разделив первое уравнение на –1,2, второе на 1,06, и вычтя из первого уравнения второе получим:

2,68  A2  21,72, откуда a2  7,9

Подставляя а₂ в любое из двух уравнений системы найдём a_l, после чего, про­изведя подстановку значений a₁ и a₂ в систему из трёх уравнений найдём значение а₀. В результате вычислений найдём: а₁  13,45 a₀  8,32

С учётом найденных значений коэффициентов уравнение производственной функции примет вид:

Y = 8,32 + 13,45x₁ + 7,9x₂

2.2.5. Определение погрешностей моделирования

Используя метод дисперсионного анализа (от лат. dispersus – рассыпанный, рассеянный) следует выяснить пригодность полученной модели.

В качестве критериев, оценивающих качество модели воспользуемся четырьмя показателями: абсолютной погрешностью (S_0cm), коэффициентом детерминации (D), индексом корреляции (I), критерием Фишера (F_Раcч).

Найдём среднюю фактически произведённую продукцию:

Для удобства дальнейших расчётов заполним таблицу:

N	Yф	Ym	(Yф – Ycp)2	(Ym – Ycp)2	(Yф – Ym)	(Yф – Ym)2
1	260	260,14	1284,3	1294,7	-0,14	0,02
2	311,2	310,9	7575,5	7520,9	0,3	0,09
3	280,5	280,5	3173,9	3173,9	0	0
4	234	234,2	96,8	101,7	-0,2	0,06
5	209	209,2	229,9	222,5	-0,2	0,06
6	172	172,3	2720,9	2685,3	-0,3	0,11
7	175,4	175,1	2377,8	2409,9	0,3	0,11
8	151,2	150,9	5323,5	5373,1	0,3	0,11
		Сумма:	22782,7	22782,1	0,06	0,56

Совокупность исходных данных Yф имеет 8 степеней свободы (n=8); совокупность расчётных данных Ym имеет 3 степени свободы (v=3); совокупность Yср имеет 1 степень свободы.

Следовательно, совокупности (Yф – Yсp) имеет 7 степеней свободы;

(Ym – Yсp) имеет 2 степени свободы;

(Yф – Ym) имеет 5 степеней свободы.

Теперь можно определить дисперсии:

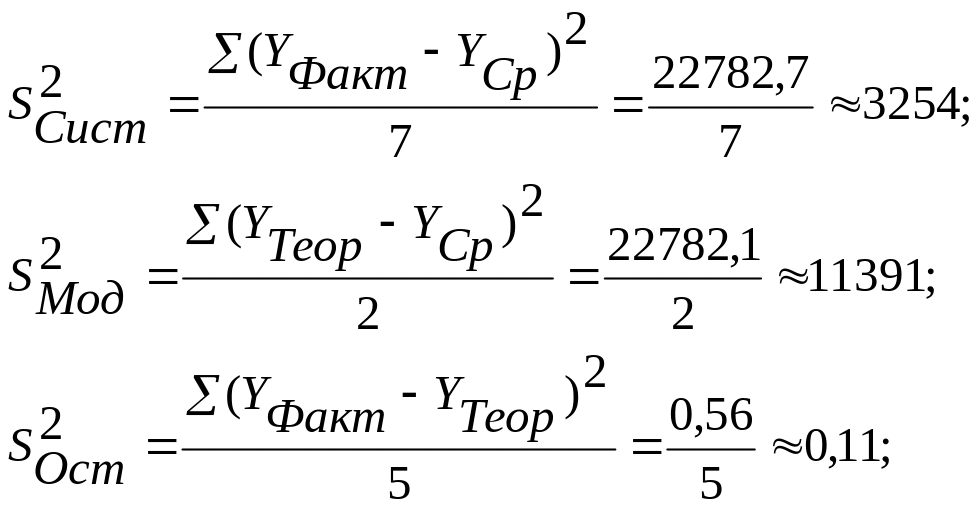
Абсолютная погрешность составит:

Коэффициент детерминации:

Индекс корреляции:

Критерий Фишера:

Вывод: Качество модели приемлемое т. к. индекс корреляции больше 0,7 и расчётный критерий Фишера больше табличного для данного случая (F_Taб = 5,8).