Лекция №8. Специфика временных рядов как источника данных в эконометрическом моделировании.

План лекции:

1. Временной ряд. Автокорреляция уровней.

2. Моделирование тенденций временного ряда.

3. Моделирование периодических колебаний.

4. Автокорреляция в остатках. Критерий Дарбина-Уотсона.

1. Временной ряд. Автокорреляция уровней.

Эконометрическую модель можно построить, используя два типа исходных данных:

• данные, характеризующие совокупность различных объектов в определенный момент (период) времени;

• данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные по данным второго типа, называются моделями временных рядов.

Временной ряд (динамический ряд, ряд динамики) – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени (табл. 1).

Таблица 1

Динамика ВВП Российской Федерации

	Годы (ti)
	2000	2001	2002	2003	2004
ВВП, млрд. руб. (yi)	7305,6	8943,6	10834,2	13285,2	17048,1

Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на три группы:

1. факторы, формирующие тенденцию ряда (Т);

2. факторы, формирующие периодические (циклические или сезонные) колебания ряда (S);

3. случайные факторы (Е).

На рис.1 представлен график временного ряда, на котором прослеживаются все три составляющие.

Рис. 1. Временной ряд

Различным образом объединяя эти компоненты, можно получить различные модели временного ряда (Y):

- аддитивную

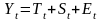
- мультипликативную

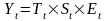
- смешанную

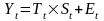
Основная задача эконометрического исследования временного ряда заключается в выявлении и придании количественного выражения его компонентам (тенденции, периодичности, случайной компоненты) в целях их использования для прогнозирования будущих значений ряда.

Перед построением модели исходные данные проверяются на сопоставимость (применение одинаковой методики получения или расчета данных), однородность (отсутствие случайных выбросов), устойчивость (наличие закономерности в изменении уровней ряда) и достаточность (число наблюдений должно в 7–10 превосходить число параметров модели).

Важной особенностью временных рядов по сравнению с данными наблюдений, относящихся к одному периоду времени, является, как правило, наличие связи между последовательными уровнями ряда, вызванное действием каких-либо долговременных причин, что приводит к наличию таких составляющих ряда, как долговременная тенденция и циклическая составляющая.

Корреляционная зависимость между последовательными уровнями временного ряда называется автокорреляцией уровней временного ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями ряда, сдвинутыми на несколько шагов назад во времени ( ):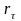

,

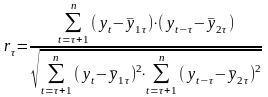где τ – величина сдвига во времени, называемая лагом.

; .

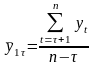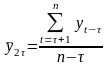Например, лаг τ=1 означает, что ряд сдвинут на один период (момент) назад и т.д. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.

Таким образом, коэффициент автокорреляции может быть первого, второго и т.д. порядка. Он измеряет зависимость между соседними уровнями ряда: первого порядка – между t и t-1 (лаг 1); второго порядка – между t и t-2 (лаг 2) и т.д.

Формулы коэффициентов автокорреляции уровней ряда первого и второго порядка примут следующий вид:

;

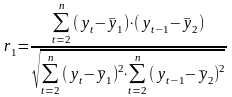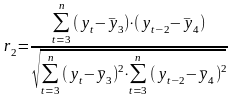
Свойства коэффициента автокорреляции:

1. он характеризует тесноту только линейной связи текущего и предыдущего уровней ряда, поэтому по данному коэффициенту можно судить о наличии линейной или близкой к линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию, коэффициент автокорреляции может приближаться к нулю;

2. по знаку коэффициента автокорреляции нельзя судить о возрастающей или убывающей тенденции в уровнях ряда.

Последовательность коэффициентов автокорреляции первого, второго и т.д. порядков называется автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага – коррелограммой.

Таблица 2

Коррелограмма временного ряда потребления электроэнергии

Лаг (квартал)	Коэффициент автокорреляции уровней	Коррелограмма
1	0,165154
2	0,566873
3	0,113558
4	0,983025
5	0,118711
6	0,722046
7	0,003367
8	0,973848

Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т.е. определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, связь между уровнями ряда наиболее тесная, а также определить присутствие в ряде той или иной компоненты, а именно:

• если наиболее высоким оказался коэффициент корреляции 1-ого порядка, ряд содержит только тенденцию (Т);

• если наиболее высоким оказался коэффициент корреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени (S);

• если ни один из коэффициентов не является значимым, ряд либо не содержит тенденции и циклических колебаний, т.е. случаен (Е), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужен дополнительный анализ.

Например, по коррелограмме в табл. 2 можно сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в 4 квартала.