

операцій. Обчислення |
власних |
значень |
матриці |
D zzT обійдеться в |
O n2 арифметичних операцій. |
Така ж кількість операцій необхідна і для |
|||
обчислення власних |
векторів |
матриці |
D zzT . |
Обчислення матриці |
Q1 Q
0
0 |
|
Q обійдеться в c |
n3 |
операцій. Таким чином, |
|
||||||||
|
|
|
|||||||||||
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
O n |
2 |
O n |
2 |
cn |
3 |
|
|
||
|
|
t n 2t |
|
|
|
|
|
. |
(18) |
||||
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Якщо матриці Q1, Q2 , Q є щільними і використовується стандартний
алгоритм матричного множення, то в формулі (18) константа c 1. Таким чином, саме операція множення є найбільш трудомісткою в алгоритмі.
Тому, ігноруючи в (18) члени порядка n2 , отримаємо
n |
|
|
3 |
|
|
t n 2t |
|
|
cn |
|
. |
|
|
||||
|
2 |
|
|
|
|
Розв’язуючи це різницеве рівняння, знайдемо, що
t n c 43 n3 .
На практиці c 1 у зв’язку з тим, що матриця Q має багато нульо-
вих елементів, а для різних типів матриць від 15 до 85 % її стовпів складають стовпці одиничної матриці. Завдяки цьому факту вдається скоротити час матричного множення.
1.7.Метод Ланцоша
Метод Ланцоша розроблено в 1950 р. Спочатку його розглядали як спосіб зведення симетричної матриці А до тридіагональної матриці Т. Основою алгоритму є тричленне рекурентне співвідношення
|
|
|
|
|
|
q j 1bj |
Aq j q j a j q j 1bj 1, |
j 1, n, |
(19) |
||
q0 0, |
|
|
|
|
|
|
|
|
|
|
|
яке отримують з матричної рівності
QnTn AQn ,
40

де Qn q1, q2 , , qn |
– ортогональна матриця, складена з векторів- |
||
|
|
|
|
стовпців q j , j 1, n ; Tn |
– тридіагональна матриця вигляду (12). |
||
Тридіагональну симетричну матрицю називають н е р о з к л а д н о ю , якщо всі елементи, що стоять під її діагоналлю, не дорівнюють нулю, тоб-
то bj 0, j 1, n 1.
Якщо Tn – нерозкладна матриця, то, не обмежуючи загальних міркувань, можна вважати, що bj 0 . Тоді на базі співвідношення (19) можна записати такий а лго р и тм п о будо ви ма тр и ц і Tn за м а тр и ц ею А .
Алгоритм 8. Для заданих симетричної матриці А порядку n, початкового вектора q1 такого, що 
 q1
q1 
 2 1, для всіх j 1, 2, , n обчистити:
2 1, для всіх j 1, 2, , n обчистити:
1.u j Aq j ;
2.a j q j , Aq j ;
3.q0 0 , rj u j q j a j q j 1bj 1 ;
4.bj 
 rj
rj 
 2 ;
2 ;
5. q j 1 rj . b j
Після n кроків у точній арифметиці отримаємо тридіагональну матрицю Tn , ортогонально подібну до вихідної матриці А, і отже, задача ви-
значення власних значень матриці А звелася до задачі знаходження власних значень для тридіагональної матриці.
Припинення (зрив) процесу може відбутися, якщо bj 0 . Це ста-
неться тоді, коли вектор q1 ортогональний принаймні до одного власного вектора матриці А. Тоді за вектор q j 1 можна взяти довільний одиничний
вектор, ортогональний до попередніх векторів q, і продовжити ітераційний процес.
Під час реалізації алгоритму 8 на ЕОМ для матриць А великої розмірності строга ортогональність векторів q j , зазвичай, зникає. Це пов’язано
з тим, що ЕОМ має скінченну розрядність, що призводить до похибок заокруглення. Для запобігання цього можна використовувати модифікацію
41
методу Ланцоша з точною переортогоналізацією, яка, на жаль, потребує значних обчислювальних затрат.
Пізніше почали використовувати так званий зр і за н и й ва р іа н т мето ду Ла нц о ша як алгоритм визначення декількох крайніх власних значень великих матриць. У ньому власні значення зрізаної тридіагональної матриці Tj j n будуть наближати шукані власні значення вихідної
матриці. Як і в будь-якому ітераційному методі, постає запитання про закінчення ітерацій, тобто на якому j треба зупинитися. Для відповіді на це запитання треба мати на увазі, що метод Ланцоша в цьому випадку є реалізацією процедури Релея–Рітца для послідовності підпросторів Крилова, завдяки чому є змога контролювати на кожному кроці точність шуканих власних значень. Для реалізації цієї процедури п р о до вжи мо п р о ц е с ,
що за да но а л го р и тмо м 8 :
6. |
Для кожного j 1, 2, , n розв’яжемо задачу на власні значення: |
||
|
T |
z j j z j . |
|
|
j |
|
|
7. |
Обчислимо |
|
|
|
y j Q |
z j , |
|
|
|
j |
|
де Qj q1, q2 , , q j . При цьому обчислюють тільки потрібні компоненти
i , zi , yi .
Пару i j , yi j називають а п р о кс и мува ль но ю п а р о ю Р е лея –
Рітц а для власної пари i , xi вихідної матриці А;
8. Якщо точність шуканих векторів задовільна, то процес завершується. Точність контролюють за допомогою оцінки
|
|
|
|
|
|
|
|
Ay y |
|
|
|
2 |
. |
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Якщо в процесі обчислень отримано, що bj 0 , то це означає, що
AQj QjTj , і обчислення завершують. У разі відшукання декількох влас-
них значень такий ранній зрив ітераційного процесу є бажаним результатом, оскільки кожне апроксимуюче власне значення i буде точним влас-
ним значенням i вихідної матриці А.
42
1.8.Сингулярний розклад матриць
Сингулярному розкладу матриць (singular value decomposition, SVD-
розклад) більше ста років. Його незалежно відкрили Белтрамі в 1873 р. і Жордан в 1874 р. для випадку квадратних матриць. В 30-ті роки XX століття Еккарт та Янг поширили цей розклад на випадок прямокутних матриць. Однак як обчислювальний засіб його стали використати набагато пізніше, в 60-ті роки. Це пов’язано з тим, що обчислення SVD вимагає застосування ряду достатньо тонких чисельних методів. Практичне використання SVD стало можливо в першу чергу завдяки Дж. Голубу, що в серії робіт продемонстрував його корисність і застосовність у багатьох областях.
Якщо А – довільна m n -матриця, при чому m n . Тоді буде справе-
дливе її представлення у вигляді: |
|
A U V T , |
(20) |
де матриця U має розмір m n і задовольняє співвідношенню U T U E ;
V – квадратна матриця порядку |
n, що задовольняє співвідношенню |
||||||
V T V E ; diag , , |
n |
, де |
|
|
n |
0 . |
|
1 |
|
1 |
|
|
|||
Стовпці u1, ,un |
матриці U називаються л і в и м и си н гу ляр ни м и |
||||||
век то р а ми ма тр и ц і А. Стовпці v1, , vn |
матриці V називаються п р а - |
||||||
ви ми си нг уляр ни ми |
век то р а ми . Величини i називаються си н гу - |
||||||
ляр ни ми чи сла ми ма тр и ц і .
Найменше сингулярне число n дорівнює відстані в 2-нормі від мат-
риці А до найближчої виродженої матриці. Кількість ненульових сингулярних чисел дорівнює рангу матриці. Отже, якщо матриця А вироджена, то
принаймні n 0  .
.
На практиці сингулярні числа рідко в точності дорівнюють нулю, однак, якщо матриця А «близька до виродженої», деякі із сингулярних чисел будуть малими. Відношення 1  n можна розглядати як число зумовленості матриці А для задачі розв’язання системи лінійних рівнянь.
n можна розглядати як число зумовленості матриці А для задачі розв’язання системи лінійних рівнянь.
При m n необхідно розглядати SVD матриці AT .
Розглянемо г ео ме тр и ч н у ін тер п р е та ц ію ви щеска за но го
твер д же ння . Будемо розглядати |
m n -матрицю А як лінійний опера- |
тор, який відображає вектор x Rn |
y вектор y Ax Rm . Тоді можна |
43

обрати ортогональну координатну систему для Rn , де ортами осей є стов-
пці матриці V, і другу ортогональну координатну систему для Rm (із стовпцями матриці U в якості ортів осей) таким чином, щоб A набула діаго-
n
нального вигляду Σ, тобто вектор x ivi відобразився б у вектор
i 1
n
y Ax i i ui .
i 1
Інше кажучи, будь-яка матриця стане діагональною, якщо обрати потрібні ортогональні координатні системи в її області визначення і області значень.
Розглянемо найбільш важливі з а л гебр а їч ни х та гео метр и ч ни х вла сти во ст ей S V D .
1. Нехай А – симетрична матриця з власними значеннями i і орто-
нормованими власними векторами u |
i |
. Іншими словами, |
A U V T є |
||
спектральним розкладом матриці А, де diag(1, , n ) , |
U u1, ,un |
||||
і U U T E . Тоді SVD-розклад матриці А має вигляд |
|
||||
|
|
A U V T , |
|
||
|
|
|
|||
де і |
і |
і vi sgn(i ) ui , причому sgn(0) 1. |
|
||
2. Власними значеннями симетричної матриці AT A |
є числа i2 . |
||||
Праві сингулярні вектори vi є відповідними ортонормованими власними векторами.
3. Власними значеннями симетричної матриці AAT |
є числа 2 і |
|
|
|
i |
m n нулів. Ліві сингулярні вектори ui |
є відповідними ортонормованими |
|
власними векторами, які відповідають |
власним числам |
2 . Додаткові |
|
|
i |
m n ортогональних векторів можна взяти в якості власних векторів для
власного значення, що дорівнює нулю. |
|
|||
|
0 |
AT |
, де А − квадратна матриця, |
|
4. Нехай H |
|
|
|
|
|
|
0 |
|
|
A |
|
|
||
що має SVD вигляду (20). Покладемо diag(1, , n ) , U u1, ,un і
V v1, , vn 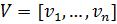 . Тоді 2n власних значень матриці Н −
. Тоді 2n власних значень матриці Н −
44
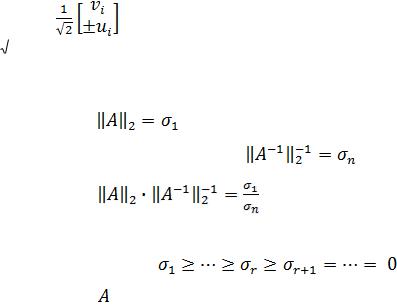
це |
|
числа |
|
i , |
|
а |
відповідні нормовані |
власні |
вектори мають |
вигляд |
||||||||||||||||||||||||||
1 |
|
|
|
|
vi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
5. |
Якщо А − матриця повного |
|
рангу, |
то |
розв’язком |
задачі |
||||||||||||||||||||||||
min |
|
|
|
|
|
2 |
є вектор x V 1 U T b . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Ax b |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
6. |
|
A |
|
|
2 |
1 |
|
|
|
|
. Якщо А − квадратна й невироджена мат- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
риця, |
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
A 1 |
|
|
|
1 |
n |
|
|
|
|
|
і |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
A 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
7. |
Припустимо, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
що |
|||||||||||||
1 r r 1 0 |
|
|
|
|
|
|
|
|
|
|
То- |
|||||||||||||||||||||||||
ді ранг матриці А |
дорівнює r. |
|
|
|
|
|
|
U u1, ,un , |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
8. |
Нехай |
матриці |
V v1, , vn |
|
і |
такі що |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A U V T |
|
i ui |
viT |
|
(сума матриць рангу 1). Тоді найближчою до |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матриці |
|
A |
|
|
|
в |
значенні |
2-норми |
|
|
матрицею |
рангу |
k n |
є матриця |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ak |
|
i ui viT , |
причому |
|
A Ak |
|
|
2 k 1 . Для матриці Ak справедливе |
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
також представлення у вигляді |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A U |
k |
V T , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||
де k diag(1, , k, 0, ,0) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
Використовуючи властивості 2 і 3, можна обчислити SVD матриці |
||||||||||||||||||||||||||||||
шляхом визначення власних значень і власних векторів матриць |
AT A і |
|||||||||||||||||||||||||||||||||||
AAT .
45

Приклад 8. Знайдемо сингулярні числа, праві та ліві сингулярні ве-
ктори матриці |
1 |
2 |
0 |
|
|
A |
|
|
|
. |
|
|
|
2 |
0 |
2 |
|
|
|
|
|||
Р о з в ' я з а н н я . |
Матриця AT A має розмір 3 3, а матриця AAT – |
||
22. Тому для розрахунків будемо використовувати матрицю AAT . |
|||
|
5 |
2 |
|
|
AAT |
|
. |
|
|
8 |
|
|
2 |
|
|
Побудуємо її характеристичний поліном:
5 8 4 2 13 36 0 .
Звідси власними значеннями матриці AAT будуть числа 1 9 і 2 4 . Сингулярні числа матриці А, отже, будуть 1 3 і 2 2 .
Ліві сингулярні вектори матриці А є власними векторами матриці AAT . Для їх отримання розглянемо системи лінійних рівнянь
1E AAT u 0;2 E AAT u 0.
Отже, вектор, пропорційний вектору 1, 2 T , є власним вектором матриці
AAT , що відповідає власному значенню 1 . Вектор, пропорційний вектору 2, 1 T , є власним вектором матриці AAT , що відповідає власному значенню 2 . Нормуємо отримані вектори. В результаті отримаємо, що
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
2 |
||
u |
|
|
|
|
|
|
, |
u |
2 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||
1 |
5 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
5 |
1 |
|||||
Таким чином, вектори u1, u2 є лівими сингулярними векторами матриці А. Не важко бачити, що вони є ортогональними.
Тепер можна визначити праві сингулярні вектори v1, v2 , v3 , обчис-
люючи власні вектори матриці AT A . Але вектори v1, v2 можна легко визначити за формулою
v 1ATu , i 1, 2 . |
|
i i |
i |
46

Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
0 |
|
|
|
||
v1 |
1 |
|
|
|
|
|
|
v2 |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
2 , |
|
|
|
|
2 |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
5 |
|
|
4 |
|
|
|
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отримані вектори є ортонормованими. Третій вектор |
v3 |
повинен |
||||||||||||||||
задовольняти умові Av3 0 . |
|
Розв’язуючи |
|
це |
рівняння |
та |
нормуючи |
|||||||||||
отриманий розв’язок, маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
v3 |
|
|
1 . |
|
|
|
|
|
|
|||||||
|
|
3 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Тепер, коли знайдено сингулярні числа і сингулярні вектори, можна легко побудувати SVD матриці А в вигляді (20), при цьому U R2 2 , V R3 3 , а R2 3 – діагональна матриця. Отже,
|
U u , u |
|
|
|
|
|
1 |
|
|
1 |
2 |
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
5 |
|||||||||
V v , v |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
, v |
3 |
|
|
|
2 |
6 |
|
5 , |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
4 |
3 |
2 |
5 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
3 |
0 |
0 |
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
0 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 2 |
0 |
|
|
|
|
|
|
|||||||||||||
Легко перевірити, що A U V T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Обчислення SVD шляхом розв’язання задачі на власні значення для |
||||||||||||||||||||||||
матриць AT A або AAT |
є продуктивним методом для великих та важних |
|||||||||||||||||||||||
практичних задач, оскільки |
|
розроблено |
ефективні |
чисельні методи |
||||||||||||||||||||
розв’язання симетричної задачі на власні значення. Однак у цього підходу є серйозні н е д о л і к и : якщо матриця А має досить малі, але відмінні від нуля сингулярні числа, то їх знаходження може виявитися неточним. Це пов’язано з обчислювальними похибками, що виникають при переході до
квадратної матриці AT A . Тому у за га л ьн ени й а лго р и тм р о зр а х у н ку
47
