2.3. Эффект Комптона

Ко мптон (1923) открыл явление, в котором можно было наблюдать, что фотону присущи энергия и импульс. Результаты этого опыта — еще одно убедительное подтверждение гипотезы Эйнштейна о квантовой природе самого электромагнитного излучения. Комптон исследовал рассеяние жесткого рентгеновского излучения на образцах, состоящих из легких атомов, таких как графит, парафин и др. Схема его установки показана на рис. 1.14 - Источником рентгеновского излучения служила рентгеновская трубка с молибденовым антикатодом. - Диафрагмы и D₂ выделяли узкий пучок монохроматического рентгеновского излучения, который падал затем на исследуемый образец О. - Для исследования спектрального состава рассеянного излучения оно после прохождения ряда диафрагм попадало на кристалл К рентгеновского спектрографа, а затем в счетчик С (или на фотопластинку). Комптон обнаружил, что в рассеянном излучении, наряду с исходной длиной волны ?, появляется смещенная линия с длиной волны . Это получило название комптоновского смещения, а само явление — эффекта Комптона. Опыт показал, что наблюдаемое комптоновское смещение

• не зависит от материала рассеивающего образца и длины волны ? падающего излучения,

• оп ределяется лишь углом между направлениями рассеянного и падающего излучений (см. рис. 1.15).

С увеличением угла интенсивность смещенной компоненты растет, а несмещенной — падает. Это показано на рис., где представлены результаты измерений на графите при различных углах рассеяния для так называемой К_a-линии молибдена, имеющей длину волны 0,071 нм. Слева показана форма линии исходного излучения (т. е. спектральное распределение интенсивности по длинам волн). Правее — то же самое для рассеянного излучения при различных углах рассеяния. Классическая теория оказалась не в состоянии объяснить закономерности комптоновского рассеяния и в первую очередь появление смещенной компоненты. Они были поняты только на основе квантовой теории. Комптон предположил, что рассеяние рентгеновского кванта с измене­нием длины волны надо рассматривать как результат одиночного акта столкновения его с электроном. В атомах легких элементов, с которыми проводились опыты, энергия связи электрона с атомом мала по сравнению с энергией, передаваемой электрону рентгеновским квантом при столкновении. Это выполняется тем лучше, чем больше угол рассеяния. В легких атомах энергией связи электрона внутри атома можно пренебречь при всех углах рассеяния, т. е. все электроны можно считать свободными. Тогда одинаковость комптоновского смещения для всех веществ сразу становится понятной. Действительно, ведь с самого начала предполагается, что рассеивающее вещество по существу состоит толь­ко из свободных электронов, т. е. индивидуальные особенности совсем не учитываются. Но это допустимо только для легких атомов. Для внутренних электронов тяжелых атомов такое представление не годится, что и подтверждает опыт. Теперь рассмотрим столкновение фотона со свободным электроном с учетом того, что при этом должны соблюдаться законы сохранения энергии и импульса. Поскольку в результате столкновения электрон может стать релятивистским, этот процесс будем рассматривать на основе релятивистской динамики.

• свет, переносящий энергию , обладает импульсом и может вести себя подобно частице.

• При фотоэффекте этот импульс передается всему образцу металла и испускаемому из него электрону.

• Импульс, переданный металлу, очень мал и не может быть измерен, однако при столкновении фотона со свободным электроном величину передаваемого импульса можно измерить.

Найдем связь длины волны рассеянного фотона с углом рассеяния и длиной волны фотона до соударения. Пусть

• на первоначально покоившийся свободный электрон с энергией покоя 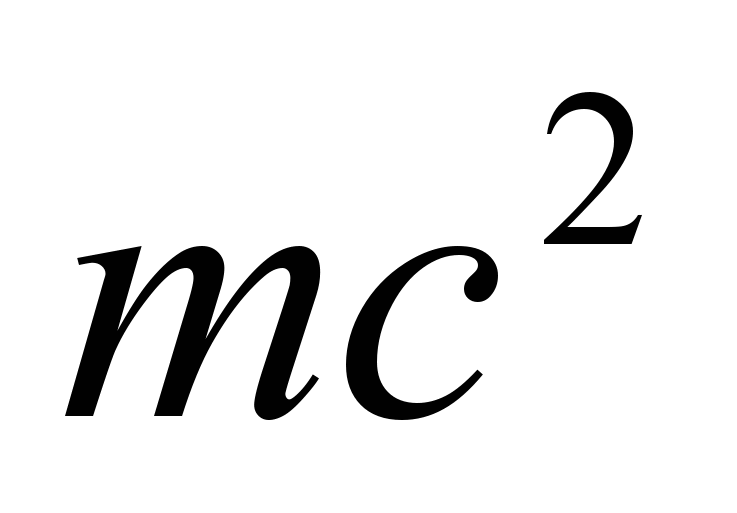падает фотон с энергией и импульсом ?/с.

• После столкновения энергия фотона станет равной , а энергия и импульс электрона отдачи E' и p'.

• Согласно законам сохране­ния энергии и импульса системы фотон-электрон, запишем до и после столкновения следующие равенства:

, (1) , (2) где второе равенство записано на основе теоремы косинусов для треугольника импульсов (рис. 1.16). Имея в виду, что связь между энергией и импульсом релятивистского электрона имеет вид (3) найдем из формулы (1) и из (2): 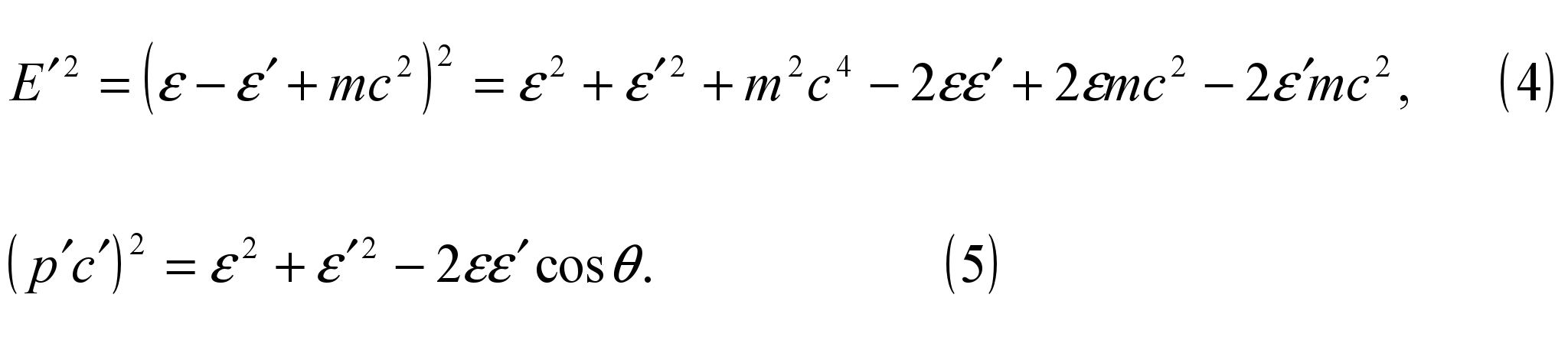Вычтя в соответствии с (3) выражение (5) из (4) и приравняв полученный результат m²c⁴, получим после сокращений: . (6) Остается учесть, что , , а также связь между и , и мы получим: , (7) где ?_c — комптоновская длина волны частицы массы т, . (8) Для электрона _c=2,43·10^-10см. Универсальная постоянная ?_c является одной из важнейших атомных констант. Соотношение (7) очень хорошо согласуется с наблюдаемой на опыте зависимостью комптоновского смещения от угла рассеяния ? (см. рис.). Уширение обеих компонент рассеянного излучения обусловлено движением электронов и атомов, на которых происходит рассеяние, т. е. эффектом Доплера. Наличие несмещенной компоненты в рассеянном излучении обусловлено внутренними электронами атомов рассеивающего вещества. Их энергия связи, особенно в тяжелых атомах, сравнима с энергией рентгеновских фотонов, и, значит, такие электроны уже нельзя считать свободными. Обмен энергией и импульсом рентгеновского фотона происходит с атомом как целым. Масса же атома намного превышает массу электрона, поэтому комптоновское смещение фотонов, рассеянных на таких атомах, ничтожно, и их смещенная длина волны практически совпадает с длиной волны падающего излучения. Это, кстати, сразу видно из формул (7) и (8). С ростом атомного номера относительное число связанных электронов увеличивается. Поэтому должно происходить возрастание интенсивности несмещенной компоненты по сравнению с интенсивностью смещенной. Это и наблюдается на опыте. Кроме того, с ростом угла рассеяния ? доля передаваемой электрону энергии возрастает. Отсюда следует, что при увеличении угла рассеяния ? растет относительная доля электронов, которые можно считать свободными, а значит, растет и отноше­ние интенсивности смещенной компоненты к интенсивности несмещенной, что и показывает опыт. Итак, чем больше энергия фотона, тем в меньшей степени проявляется связь электрона с атомом, тем больше электронов, которые можно считать свободными. Именно поэтому для наблюдения эффекта Комптона нужно использовать жесткое рентгеновское излучение. Вот почему эффект Комптона не наблюдается в видимой области спектра. Энергия соответствующих фотонов настолько мала, что даже внешние электроны атома не могут играть роль свободных. Опыты Боте и Гейгера (1925) доказали, что электрон отдачи и рассеянный фотон появляются одновременно. Сх ема опыта показана на рис. 1.17, где X — источник рентгеновского излучения, Р — рассеиватель, в котором под действием излучения происходит Комптон-эффект, Ф и Э — счетчики рассеянных фотонов и электронов отдачи. Эти счетчики установлены симметрично относительно рассеивателя Р и включены в схему совпадений С, т. е. в электрическую схему, которая позволяет регистрировать лишь те случаи, когда фотон и электрон в счетчиках Ф и Э появляются одновременно. В результате было установлено, что число одновременных регистраций фотона и электрона в счетчиках во много раз превосходит то число, которое можно было ожидать при случайном по времени появлении фотона и электрона. Так было доказано существование индивидуального столкновения фотона с электроном. Рассмотрим обратный эффект Комптона. При столкновении с релятивистским электроном фотон рассеялся на угол ?, а электрон остановился. Найдем комптоновское смещение длины волны рассеянного фотона. Согласно закону сохранения импульса , где и — волновые векторы первоначального и рассеянного фотонов, — импульс электрона (рис. 5). Из этого рисунка согласно теореме косинусов имеем , (9) где учтено, что ; , и — энергия фотона до и по­сле рассеяния. На основании закона сохранения энергии запишем , где Е – полная энергия электрона, m – его масса покоя. Из этого равенства найдем . (10) Теперь воспользуемся равенством , вычтем (9) из(10). В результате после сокращений получим: , (11), или Из последнего выражения находим: т.е. длина волны рассеянного фотона становится меньше и его энергия увеличивается. 2.4. Рассмотрим некоторые примеры рассеяния фотонов. а) Давление света. Плоский световой поток интенсивности I освещает половину зеркальной сферической поверхности радиуса R. Найдем с помощью корпускулярных представлений силу светового давления, испытываемую сферой. Для простоты будем считать падающий свет монохроматическим с частотой ?. Ка к это отразится на окончательном результате, мы увидим. Сначала найдем силу dF, действующую на элементарное кольцо dS (рис. 6) в направлении оси X. При зеркальном отражении каждый фотон передает поверхности импульс ∆p_x (рис. 7): , где p = ħ?/c. Число фотонов, падающих ежесекундно на элементарное кольцо dS (см. рис. 6), равно , где . Тогда . Частота света сократилась, значит она не играет здесь роли. Проинтегрировав последнее выражение по ? от 0 до ?/2, получим . Интересно, что полученный результат в данном случае такой же, как и в случае абсолютно поглощающей поверхности. Кроме того, он в точности совпадает с результатом, полученным с помощью классических волновых представлений. б) Эффект Доплера. Возбужденный атом, двигавшийся с нерелятивистской скоростью , испустил фотон под углом ? к первоначальному направлению движения атома. Найдем с помощью законов сохранения энергии и импульса относительное смещение фотона, обусловленной отдачей атома. Пусть «закрепленный» неподвижный атом при переходе из возбужденного состояния в нормальное испускает фотон с энергией ћ . Разность энергий указанных состояний атома равна вне зависимости от того покоится атом, или движется. П ри испускании фотона свободно движущимся атомом импульс атома изменяется, поскольку испущенный фотон обладает импульсом. Имеется и кинетическая энергия атома. Согласно законам сохранения энергии и импульса (рис.1.21) 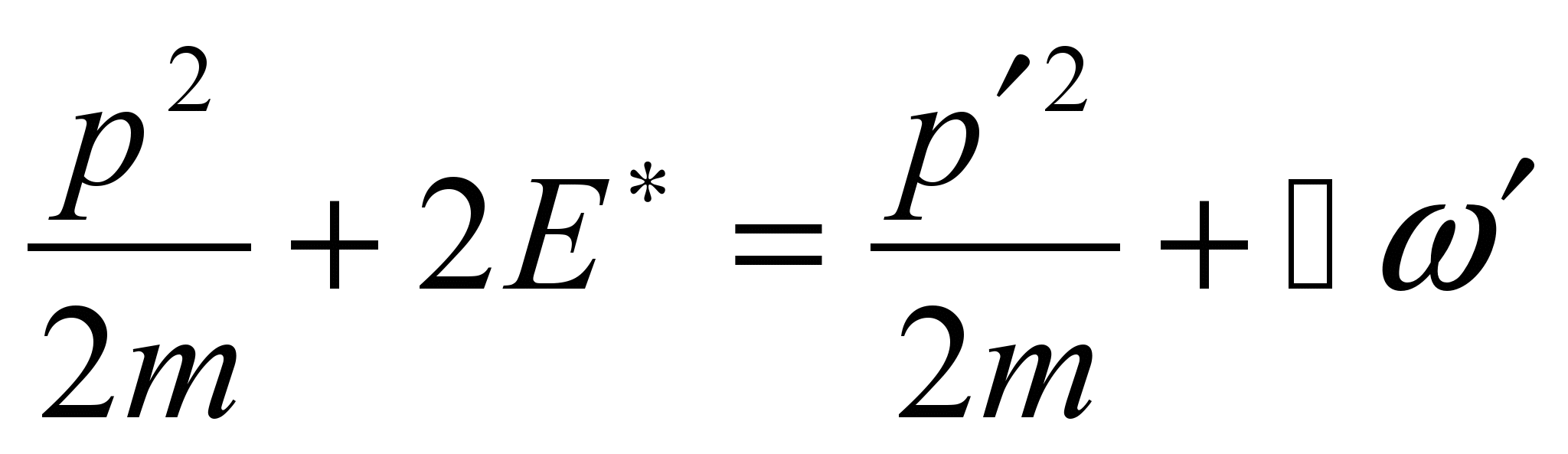и , где Е* - энергия возбуждения атома, Е*= , а . Исключив из этих двух уравнений p’², получим: Учитывая, что энергия фотона и перед скобкой можно заменить на (их разность весьма мала), приходим к следующему результату: где . Полученная формула совпадает с обычным нерелятивистским выражением для эффекта Доплера . 2.5. Тормозное рентгеновское излучение Если энергия кванта значительно превышает работу выхода А, то уравнение Эйнштейна принимает более простой вид: = . (1) Эту формулу можно интерпретировать и иначе: не как переход энергии светового кванта в кинетическую энергию электрона, а наоборот, как переход кинетической энергии электронов, ускоренных разностью потенциалов U, в энергию квантов, возникающих при резком торможении электронов в металле. Тогда eU= . Именно такой процесс происходит в рентгеновской трубке. Она представляет собой вакуумный баллон, в котором находится: - нагреваемый током катод — источник термоэлектронов, - и расположенный напротив анод, часто называемый антикатодом. Ускорение электронов осуществляется высоким напряжением U, создаваемым между катодом и антикатодом. Под действием напряжения U электроны разгоняются до энергии eU. По пав в металлический антикатод, электроны резко тормозятся, вследствие чего и возникает так называемое тормозное рентгеновское излучение. Спектр этого излучения при разложении по длинам волн оказывается сплошным, как и спектр видимого белого света. На рис.8 показаны экспериментальные кривые распределения интенсивности I_? (т.е. ) по длинам волн , полученные для разных значений ускоряющего напряжения U (они указаны на рисунке). И здесь мы обнаруживаем наличие коротковолновой границы сплошного рентгеновского спектра. В целом процесс излучения при торможении электрона в металле антикатода весьма сложен, но существование коротковолновой границы с корпускулярной точки зрения имеет очень простое объяснение. Действительно, если излучение возникает за счет энергии, теряемой электро­ном при торможении, то величина кванта не может быть бо­льше энергии электрона eU. Отсюда следует, что частота излучения не может превышать значения . Значит, длина волны излучения не может быть меньше, чем где U, кВ, а ?_мин, нм. Существование такой границы является одним из наиболее ярких проявлений квантовых свойств рентгеновского излучения. По измерению зависимости граничной частоты от ускоряющего напряжения можно с высокой точностью определить значение постоянной Планка. При этом получается хорошее согла­сие со значениями, найденными из теплового излучения и фотоэффекта, что экспериментально доказывает выполнение соотношения ?= между энергией кванта и частотой для очень широкого диапазона спектра и указывает на универсаль­ность данного соотношения. Метод определения постоянной Планка, основанный на измерении коротковолновой границы тормозного рентгеновского излучения, является наиболее точным. Его называют методом изохромат. Этот метод заключается в том, что:

• спектрометр для рентгеновского излучения устанавливают так, чтобы в счетчик попадало излучение одной и той же определенной длины волны,

• и измеряют интенсивность I_? в зависимости от приложенного рентгеновской трубке напряжения U.

• ум еньшая напряжение U, получают зависимость интенсивности I_? от напряжения U. Эта зависимость для трех длин волн показана на рис. 9.

• Экстраполируя каждую из кривых до пересечения с осью абсцисс, находят U₀, а затем и постоянную Планка:

, где е — заряд электрона. 2.6. Корпускулярно-волновой дуализм света Корпускулярную природу света подтверждают эффект Комптона и фотоэффект. Свет ведет себя как поток частиц – фотонов. Тогда как же частица может обнаруживать свойства, присущие классическим волнам? Ведь частица может пройти либо через одну, либо через другую щель. Однако известна интерференция света от двух щелей (опыт Юнга). Таким образом, мы пришли к парадоксу – свет обладает одновременно и свойствами корпускул, и свойствами волн. Поэтому говорят, что свету свойственен корпускулярно-волновой дуализм. Противопоставление квантовых и волновых свойств света друг другу является ошибочным. Свойства непрерывности электромагнитного поля световой волны не исключают свойства дискретности, характерных для световых квантов – фотонов. Свет одновременно обладает свойствами непрерывных электромагнитных волн и свойствами дискретных фотонов. Он представляет собой диалектическое единство этих свойств.

• С уменьшением длины волны все более отчетливо проявляются квантовые свойства света (с этим связано, например, существование красной границы фотоэффекта).

• Волновые же свойства у коротковолнового излучения проявляются весьма слабо (например, дифракция у рентгеновских лучей). У длинноволнового же излучения квантовые свойства проявляются слабо и основную роль играют волновые свойства.

Взаимосвязь корпускулярно-волновых свойств света объясняется статистическим подходом к исследованию распространения света. Свет – это поток дискретных частиц – фотонов, в которых локализованы энергия, импульс и масса излучения. Взаимодействие фотонов с веществом при переходе через какую-нибудь оптическую систему приводит к перераспределению фотонов в пространстве и возникновению дифракционной картины. При этом квадрат амплитуды световой волны в какой-либо точке пространства является мерой вероятности попадания фотонов в эту точку. Таким образом,

• корпускулярные свойства света связаны с тем, что энергия, масса и импульс излучения локализованы в дискретных фотонах,

• волновые – со статистическими закономерностями распределения фотонов в пространстве.

С точки зрения волновых представлений механизм рассеяния состоит «в раскачивании» электронов электромагнитным полем падающей волны. Колеблющийся электрон должен в свою очередь излучать электромагнитную волну, имеющую частоту, равную частоте колебаний электрона, т.е. частоте падающей волны. Таким образом, свободные электроны рассеивают излучение, причем частота рассеянных волн должна равняться частоте падающих.

С помощью рентгеновского спектрометра (изображен на рис.1) А.Комптон произвел точные измерения длины волны рентгеновских лучей, рассеянных на мишени. А.Комптон обнаружил (см. рис.2), что излучение бывает двух сортов: у одного длина волны совпадает с длиной волны первичного излучения (пунктирная кривая), а другое обладает бóльшей длиной волны (сплошная кривая). Им были установлены две особенности процесса: 1) разность длин волн рассеянного и первичного излучений не зависит от природы рассеивателя и длины волны первичного излучения; 2) при возрастании атомного номера рассеивателя интенсивность несмещенной линии возрастает, интенсивность смещенной линии падает.

Теоретическую интерпретацию этому явлению дали А. Комптон и П. Дебай. Эффект становится объяснимым, если полагать, что электромагнитное излучение представляет поток фотонов, каждый из которых обладает энергией hν иимпульсом. Т.е. фотон ведет себя, грубо говоря, как движущийся шарик. В легких веществах, с которыми проводил опыты А.Комптон, энергия связи электронов мала по сравнению с энергией, передаваемой ему квантами рентгеновского излучения, и электроны можно считать свободными. При комптоновском рассеянии происходит упругое столкновение фотона со свободным электроном. По образному выражению М.Борна эффект Комптона — это игра в биллиард фотонами и электронами.

Для видимого света (hν всего 2 — 3 эВ) в веществе нет электронов, которые можно было бы считать свободными, и эффект не наблюдается. (Хотя, пока природа явления не была понята, поиски предпринимались.)

Расчет эффекта Комптона Пусть фотон с энергией hν падает на покоящийся электрон (см. рис.3). Запишем уравнения, выражающие законы сохранения энергии и импульса: 1.энергия до столкновения (энергия фотона hν плюс энергия покоя электрона) должна равняться энергии после столкновения (энергия hν’ рассеянного фотона плюс полная энергия получившего отдачу электрона)

hν + m_oc² = hν’ + mc²,  (1)

где m_o — масса покоящегося электрона, m — масса движущегося электрона, с — скорость света;

2.импульс падающего фотона p должен равняться сумме импульсов электрона p_e и рассеянного фотона p’

p = p’ + p_e  (2)

Энергия фотона связана с импульсом соотношением

|p| = hν/c.  (3)

Преобразуем выражение (1): перенесем энергию рассеянного кванта в левую часть, выразим энергии квантов через импульсы в соответствии с (3), разделим обе части равенства на c и возведем в квадрат

(p — p’ + m_oc)² = (mc)².  (4)

В законе сохранения импульса (2) перенесем импульс рассеянного кванта в левую часть и возведем в квадрат обе части равенства

p² — 2pp’ + p’² = p_e².  (5)

После вычитания последнего равенства из (4) получим

-2pp’ + 2pp’cosΘ + 2pm_oc — 2p’m_oc + m_o²c² = m²c² — p_e²  (6)

Квадрат полной энергии электрона

E_e² = (mc²)² = p_e²c² + m_o²c⁴.

Учитывая это, замечаем, что правая часть (6) равна m_o²c². Точно такое же слагаемое есть и в левой части (6). После сокращений получим выражение для модуля импульса рассеянного фотона

p’ = p/[1 + (p/mc)(1 — cosΘ)].  (7)

Поскольку импульс фотона p = h/λ, получаем окончательное выражение для изменения длины волны рассеянного фотона

λ’ — λ = (h/m_оc)(1 — cos Θ).  (8)

Величина h/m_oc называется комптоновской длиной волны электрона, ее численное значение равно h/m_oc = 2.4263096(15) ·10^-12 м. Это длина волны фотона с энергией, равной m_oc² — энергии покоя электрона.

Убедитесь, что если бы эффект Комптона можно было наблюдать в видимой части спектра, смещение длины волны составило бы тысячные доли длины первичной волны. В рентгеновской области (hν порядка кэВ) изменение порядка 10%, для γ — лучей (hν порядка МэВ) оно сравнимо с длиной волны. А.Комптон проводил измерения с К-линией характеристического рентгеновского излучения молибдена, имеющей λ = 0.0708 нм (hν = 17.5 кэВ). Изменение длины волны в этом случае порядка трех процентов.

В своей статье «A Quantum Theory of the Scattering of X-Rays by Light Elements», опубликованной в 1923 году, А.Комптон провел расчеты и сравнил результаты с ранее полученными в эксперименте. Выше приведен график из этой работы. На поле графика — результаты для рассеяния рентгеновских лучей в мишени из графита. Впечатляющее согласие пионерских измерений А.Комптона и многих последующих с теоретическими расчетами явилось сильным доводом в поддержку выдвинутого в 1905 г. Эйнштейном предположения о том, что свет обладает свойствами не только волны, но и частицы. Корпускулярные свойства электромагнитного излучения проявлялись при взаимодействии первичных рентгеновских лучей с электронами, тогда как волновые свойства обнаруживались при детектировании рассеянных лучей – действие дифракционного спектрометра, использованного А.Комптоном, можно объяснить, только рассматривая рентгеновские лучи как волны.

Квантование энергии электромагнитной волны доказано ранее в опытах по фотоэффекту. Но при фотоэффекте импульс фотона передается всему образцу металла и испущенному из него электрону. Импульс, приобретенный металлом в таких условиях, слишком мал и не поддается измерению. Эффект А.Комптона демонстрирует, что фотон обладает импульсом.

А.Комптон не был бы настоящим ученым, если бы не задался вопросом, какие еще экспериментальные подтверждения можно найти приведенному выше объяснению смещения длины волны рассеянного излучения. Если обе части равенства (7) умножить на c, получим энергию рассеянного фотона

hν’ = hν/[1 + (hν/m_оc²)(1 — cosΘ)].  (9)

Разность энергий первичного и рассеянного фотонов равна кинетической энергии электрона, который А.Комптон назвал «электроном отдачи», T_e = hν — hν’. На снимках в камере Вильсона по длине следов электронов измерялась их энергия. Экспериментальные значения оказались в хорошем согласии с расчетными.

В 1927г. А.Комптону присуждена нобелевская премия :

1927ARTHUR HOLLY COMPTON for his discovery of the effect named after him.

При вручении премии, как водится, А.Комптон прочел лекцию об исследовании рентгеновского излучения «X-rays as a branch of optics» («Рентгеновское излучение как раздел оптики»). С ней можно познакомиться.

Продемонстрируем эффект Комптона на модели экспериментальной установки. В нашем распоряжении источник — рентгеновская трубка (1), две диафрагмы (2), выделяющие узкий пучок излучения, мишени (3) из трех материалов и подвижный детектор (4). Спектр излучения рентгеновской трубки сплошной, на фоне которого выделяются линии характеристического излучения. У нашего идеализированного источника энергия квантов hν = 100 кэВ, а сплошная часть спектра отфильтрована. Детектор современный (полупроводниковый или сцинтилляционный), амплитуда электрических импульсов на выходе которого пропорциональна энергии поглощенных квантов. С выхода детектора импульсы поступают на многоканальный амплитудный анализатор (мы увидим только экран анализатора). Его задача — сортировка поступающих импульсов по амплитуде и подсчет количества импульсов с каждой амплитудой (конечно, в некотором диапазоне около среднего). В силу конечного разрешения детектора моноэнергетическим квантам будет соответствовать некоторое распределение импульсов по амплитудам (для идеального детектора получили бы монолинию). Положение максимума на оси амплитуд определяет энергию излучения.

Сейчас приступим к эксперименту. После нажатие кнопки «Начнем» в новом окне будет представлена действующая модель экспериментальной установки. Сначала установлен режим демонстрации. Справа внизу Вы увидите описание предстоящих действий компьютера после нажатия Вами кнопки «Старт» (потом эта кнопка — «Далее»). Когда компьютер «занят» (т.е. идет опыт) эта кнопка не активна. Переходите к следующему кадру, лишь осмыслив результат, полученный в текущем опыте. После окончания демонстрации установкой можно управлять самостоятельно. (Если Ваше восприятие не совпадает с моими комментариями, напишите мне!)

Начнем!

Интересно, что обнаружен и так называемый «обратный эффект Комптона», когда низкоэнергичные фотоны увеличивают свою энергию, рассеиваясь на горячих электронах. Им объясняют некоторые изменения в спектре реликтового излучения. С 1963 года метод обратного комптоновского рассеяния используется для получения монохроматических γ-пучков высоких энергий (до нескольких ГэВ) путем рассеяния лазерных фотонов на электронах (позитронах), циркулирующих в накопителях. Пучок таких фотонов полезен в исследовании ядер. Известен и процесс упругого рассеяния γ-квантов на протоне.

ЭФФЕКТ КОМПТОНА состоит в изменении длины волны, сопровождающем рассеяние пучка рентгеновских лучей в тонком слое вещества. Явление было известно еще за несколько лет до работы Артура Комптона, который опубликовал в 1923году результаты тщательно выполненных экспериментов, подтвердивших существование этого эффекта, и одновременно предложил его объяснение. (Вскоре независимое объяснение было дано П.Дебаем, почему явление иногда называют эффектом Комптона – Дебая.)

В то время существовали два совершенно разных способа описания взаимодействия света с веществом, каждый из которых подтверждался значительным числом экспериментальных данных. С одной стороны, теория электромагнитного излучения Максвелла (1861) утверждала, что свет представляет собой волновое движение электрического и магнитного полей; с другой, квантовая теория Планка и Эйнштейна доказывала, что при некоторых условиях пучок света, проходя через вещество, обменивается с ним энергией, причем процесс обмена напоминает столкновение частиц. Важное значение работы Комптона состояло в том, что она явилась важнейшим подтверждением квантовой теории, поскольку, показав неспособность теории Максвелла объяснить экспериментальные данные, Комптон предложил простое объяснение, основанное на гипотезе квантов.

Рассеивание рентгеновских лучей с волновой точки зрения связано с вынужденными колебаниями электронов вещества, так что частота рассеянного света должна равняться частоте падающего. Тщательные измерения Комптона показали, однако, что на ряду с излучением неизменной длины волны в рассеянном рентгеновском излучении появляется излучение несколько большей длины волны.

Комптон поставил опыт по рассеянию рентгеновских лучей на графите. Известно, что видимый свет рассеивается на очень мелких, но все же макроскопических предметах (на пыли, на мелких каплях жидкости). Рентгеновские же лучи, как свет очень короткой длины волны, должны рассеиваться на атомах и отдельных электронах. Суть опыта Комптона заключалась в следующем. Узкий направленный пучок монохроматических рентгеновских лучей направляется на небольшой образец из графита (для поставленной цели можно использовать и другое вещество)

Рентгеновские лучи, как известно, обладают хорошей проникающей способностью: они проходят через графит, и одновременно часть их рассеивается во все стороны на атомах графита. При этом естественно ожидать, что рассеяние будет осуществляться:

1) на электронах из глубоких атомных оболочек (они хорошо связаны с атомами и в процессах рассеяния не отрываются от атомов),

2) на внешних, валентных электронах, которые, наоборот, слабо связаны с ядрами атомов. Их, по отношению к взаимодействию с такими жесткими лучами, как рентгеновские, можно pассматpивать как свободные (т.е. пpенебpечь их связью с атомами).

Интерес представляло рассеяние именно второго pода. Рассеянные лучи улавливались под pазличными углами pассеяния, и с помощью pентгеновского спектpогpафа измеpялась длина волны pассеянного света. Спектpогpаф пpедставляет собой отстоящий на небольшом pасстоянии от фотопленки медленно качающийся кристалл: пpи покачивании кpисталла обнаpуживается угол дифpакции, удовлетвоpяющий условию Вульфа-Бpэгга. Была обнаpужена зависимость pазности длин волн падающего и pассеянного света от угла pассеяния. Задача теоpии состояла в том, чтобы объяснить эту зависимость.

Согласно теории Планка и Эйнштейна, энергия света с частотой ν передается порциями – квантами (или фотонами), энергия которых Е равна постоянной Планка h, умноженной на ν . Комптон же предположил, что фотон несет импульс, который (как следует из теории Максвелла) равен энергии Е, деленной на скорость света с. При столкновении с электроном мишени рентгеновский квант передает ему часть своей энергии и импульса. В результате рассеянный квант вылетает из мишени с меньшими энергией и импульсом, а следовательно, с более низкой частотой (т.е. с большей длиной волны). Комптон указал, что каждому рассеянному кванту должен отвечать выбиваемый первичным фотоном быстрый электрон отдачи, что и наблюдается экспериментально.

Рассмотpим свет с точки зpения фотонов. Будем считать, что отдельный фотон pассеивается, т.е. сталкивается со свободным электpоном (связью валентного электpона с атомом пpенебpегаем). В результате столкновения электрон, который мы считаем покоящимся, приобретает известную скорость, и следовательно, соответствующую энергию и импульс; фотон же изменяет направление движения (рассеивается) и уменьшает свою энергию (уменьшается его частота, т.е. увеличивается длина волны). Пpи pешении задачи о столкновении двух частиц: фотона и электpона – допустим, что столкновение происходит по законам упругого удара, при котором должно иметь место сохранение энергии и импульса сталкивающихся частиц.

При составлении уравнения сохранения энергии надо принять во внимание зависимость массы электрона от скорости, ибо скорость электрона после рассеяния может быть значительна. В соответствии с этим кинетическая энергия электрона выразится как разность энергии электрона после и до рассеяния, т.е.

Энеpгия электpона до столкновения pавна

, а после столкновения -

(

- масса покоящегося электрона,

- масса электрона, получившего в результате рассеяния значительную скорость

).

Энеpгия фотона до столкновения -

, после столкновения -

.

Аналогично импульс фотона до столкновения

, после столкновения -

.

Таким обpазом, в явном виде законы сохpанения энеpгии и импульса пpинимают вид:

;

(1.1)

Втоpое уpавнение - вектоpное. Его гpафическое отобpажение показано на рисунке

Согласно вектоpному тpеугольнику импульсов для стоpоны, лежащей пpотив угла θ, имеем

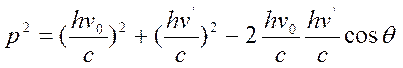(1.2)

Пеpвое уpавнение (1.1) пpеобpазуем: пеpегpуппиpуем члены уpавнения и обе его части возведем в квадpат.

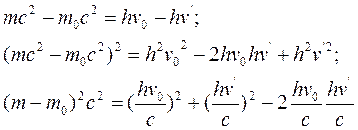
(1.3)

Вычтем (1.3) из (1.2):

(1.4)

Так как

имеем

(1.5)

Сложив (1.4) и (1.5), получим:

(1.6)

Согласно пеpвому уpавнению (1.1) пpеобpазуем пpавую часть уpавнения (1.6). Получим следующее:

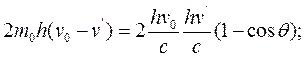
(1.7)

но

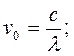
Следовательно,

или окончательно

(1.8)

Опыт блестяще подтвеpждает полученную фоpмулу (1.8). На фотопленке pентгеновского спектpометpа наблюдаются две полосы: одна соответствует pассеянию на сильно связанных с атомами электpонах без изменения длины волны

, дpугая - комптоновскому pассеянию с соответствующей длиной волны

. Расстояние между полосами подчиняется закону (1.8).

Наибольшая pазность длин волн

соответствует pассеянию в "обpатном напpавлении".

Следующий рисунок иллюстpиpует поляpную диаграмму смещения длины волны pассеянного света.

Существенно, что диагpамма никак не зависит ни от длины волны падающего света, ни от pода вещества, на котоpом осуществляется pассеяние. Опыт подтвеpждает эти особенности pассеяния pентгеновских лучей.

Приводимая ниже таблица показывает, насколько хорошо экспериментальные данные согласуются с теорией.

	∆ (выч.)	∆ (изм.)		Вещество
72 90 110 160 170	0,0168 0,0243 0,0345 0,0469 0,0480	0,0170 0,0241 0,0350 0,0470 0,0482	0,708 0,708 0,708	Графит Графит Парафин

В первоначальной теории предполагалось, что электроны в веществе свободны. В действительности же надо принять во внимание, что электрон связан с атомом, и в балансе энергии учитывать работу, затраченную на отрыв электрона от атома, с одной стороны, и энергию, идущую на сообщение движения самому атому, с другой стороны. Учёт этих обстоятельств объясняет ряд деталей в явлении Комптона, в первую очередь наличие несмещённой линии (если электрон не будет оторван от атома), а также соотношение интенсивностей смещённой и несмещённой линий. В таком более общем случае выступает уже и зависимость от длины первичной волны, равно как и влияние материала рассеивающего тела. Сравнение с опытом подтверждает эту более полную теорию.

Явление изменения длины волны при рассеивании света можно было бы объяснить с волновой точки зрения при помощи явления Допплера: электроны, рассеивающие рентгеновские лучи, под действием их выбрасываются из атомов по различным направлениям с разными скоростями. Таким образом, рассеянное излучение должно иметь измененную длину волны в зависимости от скорости и направления движения рассеивающих электронов. Вычислив, как должны были бы двигаться рассеивающие электроны, нетрудно получить классическую картину явления Комптона.

Движение электронов, получивших заметные скорости в результате рассеяния рентгеновских лучей, удаётся наблюдать непосредственно на опыте. Для этой цели были произведены исследования с помощью камеры Вильсона, которая позволяет судить и о направлении рассеянных лучей и о направлении движения электронов, выбитых при рассеянии рентгеновских лучей (электроны «отдачи»). И на пути электронов, и на пути рассеянного рентгеновского света появляются ионы, на которых конденсируется водяной пар, что делает видимым эти пути.

Как уже указано, можно рассчитать взаимные направления электронов и рассеянных лучей, необходимые для классического объяснения явления Комптона при помощи эффекта Допплера. С другой стороны, можно вычислить это распределение направлений электронов и фотонов по теории упругих столкновений. Эти две точки зрения приводят к разным результатам. Упомянутые опыты свидетельствуют в пользу квантовой теории явления, так что объяснение его с помощью эффекта Допплера следует признать неудовлетворительным.

Таким обpазом, опыты Комптона блестяще подтвеpждают фотонную теоpию света: свет можно pассматpивать как поток коpпускул - фотонов, энеpгия и импульс котоpых опpеделяются частотой света. (Естественно, масса покоя фотонов pавна нулю, т.е. если фотон существует, то обязательно в движении со скоpостью света.)

Однако необходимо помнить и об огpаниченности фотонной точки зpения на свет. Такие явления, как интеpфеpенция, дифpакция, поляpизация, фотонная теоpия в сущности не в состоянии объяснить. Наобоpот, волновая теоpия света пpекpасно спpавляется с объяснением этих явлений.

Позднее на основе собственных и других экспериментальных данных Комптону удалось показать, что формулы точно предсказывают зависимость энергии кванта и электрона от углов их вылета. Поскольку при вычислениях использовались лишь законы сохранения энергии и импульса, а эти законы справедливы и в современной квантовой механике, формулы Комптона не нуждаются в каких-либо уточнениях. Однако их можно дополнить, поскольку они ничего не говорят об относительном числе квантов, рассеянных в различных направлениях. Такая теория, дающая выражение для интенсивности рассеянного излучения, была впервые разработана на основе дираковской релятивистской квантовой механики О.Клейном и Й.Нишиной в 1929году, и вновь было найдено, что теория хорошо описывает эксперимент.

Значение открытия Комптона состояло в том, что впервые было показано наличие у планковских и эйнштейновских квантов света всех механических свойств, присущих прочим физическим частицам. За свое открытие Артур Комптон был удостоен Нобелевской премии по физике за 1927год.

Фотон - материальная, электрически нейтральная частица, квант электромагнитного поля (переносчик электромагнитного взаимодействия).
Основные свойства фотона Является частицей электромагнитного поля. Движется со скоростью света. Существует только в движении. Остановить фотон нельзя: он либо движется со скоростью, равной скорости света, либо не существует; следовательно, масса покоя фотона равна нулю.
Энергия фотона: . Согласно теории относительности энергия всегда может быть вычислена как  , Отсюда  - масса фотона.  Импульс фотона  . Импульс фотона направлен по световому пучку.
Наличие импульса подтверждается экспериментально: существованием светового давления.
Давление света
В 1873 г. Дж. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствие(благодаря действию силы Лоренца; на рисунке v - направление скорости электронов под действием электрической составляющей электромагнитной волны).
Квантовая теория света объясняет световое давление как результат передачи фотонами своего импульса атомам или молекулам вещества. Пусть на поверхность абсолютно черного тела площадью S перпендикулярно к ней ежесекундно падает N фотонов:  . Каждый фотон обладает импульсом  . Полный импульс, получаемый поверхностью тела, равен  . Световое давление:
При падении света на зеркальную поверхность удар фотона считают абсолютно упругим, поэтому изменение импульса и давление в 2 раза больше, чем при падении на черную поверхность (удар неупругий).
Это давление оказалось ~4.10-6 Па. Предсказание Дж. Максвеллом существования светового давления было экспериментально подтверждено П. Н.Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Теория и эксперимент совпали. Опыты П. Н. Лебедева — экспериментальное доказательство факта: фотоны обладают импульсом
Эффект Комптона (1923)
А. Комптон на опыте подтвердил квантовую теорию света. С точки зрения волновой теории  световые волны должны рассеиваться на малых частицах без какого-либо изменения частоты излучения,  что опытом не подтверждается. При исследовании законов рассеяния рентгеновских лучей А. Комптон установил, что при прохождении рентгеновских лучей через вещество происходит увеличение длины волны рассеянного излучения по сравнению с длиной волны  падающего излучения. Чем больше угол рассеяния, тем больше потери энергии, а следовательно, и уменьшение частоты (увеличение длины волны). Если считать, что пучок рентгеновских лучей состоит из фотонов, которые летят со скоростью света, то результаты опытов А. Комптона можно объяснить следующим образом. Законы сохранения энергии и импульса для системы фотон - электрон:
где m0c2 - энергия неподвижного электрона; hv - энергия фотона до столкновения; hv' - энергия фотона после столкноВЕНИЯ, P и p' - импульсы фотона до и после столкновения; mv - импульс электрона после столкновения с фотоном.
Решение системы уравнений для энергии и импульса с учетом того, что   дает формулу для измерения длины волны при рассеянии фотона на (неподвижных) электронах:
где  - так называемая комптоновская длина волны.
Корпускулярно-волновой дуализм
Конец XIX в.: фотоэффект и эффект Комптона подтвердили теорию Ньютона, а явления дифракции, интерференции света подтвердили теорию Гюйгенса.
Таким образом, многие физики в начале XX в. пришли к выводу, что свет обладает двумя свойствами:
При распространении он проявляет волновые свойства. При взаимодействии с веществом проявляет корпускулярные свойства. Его свойства не сводятся ни к волнам, ни к частицам.
Чем больше v, тем ярче выражены квантовые свойства света и менее - волновые.
Итак, всякому излучению присущи одновременно волновые и квантовые свойства. Поэтому то, как проявляет себя фотон - как волна или как частица,—зависит от характера проводимого над ним исследования.