1. Понятие электростатического поля.

Все тела в природе способны электризоваться, т.е. приобретать заряд. Наличие электрического заряда проявляется в том, что заряженные тела взаимодействуют друг с другом. Существует два типа электрических зарядов, условно названных отрицательными и положительными. Носителями отрицательного заряда являются в основном электроны; ядра атомов заряжены положительно. Полагают, что существование этих двух типов заряда является проявлением симметрии природы (как, например, левое и правое). Другим фундаментальным свойством заряда является его дискретность, его кратность, хоть и малой, но вполне определенной величине. В электрически изолированной системе общий заряд системы не изменяется (закон сохранения заряда). Поле, создаваемое электрическими зарядами и обнаруживающее себя воздействием на другие заряды называется электрическим полем. Если заряды неподвижны и поле не изменяется, то поле называется электростатическим.

Взаимодействие зарядов описывается законом Кулона. Если расстояние между заряженными телами много больше размеров тел, заряды можно считать точечными.

Закон Кулона. Сила взаимодействия точечных неподвижных зарядов в вакууме прямо пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними. Для одноименных зарядов (рис. 16.1)

	где  - коэффициент пропорциональности,   - электрическая постоянная (  Ф/м);
Рис. 16.1

,  - величины электрических зарядов;   – расстояние между зарядами;  – единичный вектор;  – сила, действующая на заряд   со стороны заряда  . Знак «-» обусловлен тем, что сила   направлена противоположно вектору  .

Пример использования закона Кулона.

Задача. Найти силу взаимодействия заряженного стержня с зарядом   и длиной  с точечным зарядом  , находящимся на расстоянии   от края стержня на одной прямой с ним. Дано:  . Найти:
	Рис. 16.2

Решение. Разобьем стержень (рис. 16.2) на дифференциально малые элементы длиной   с зарядом  , которые мы можем считать точечными. Сила взаимодействия заряда   с   по закону Кулона  . Представим   как заряд, приходящийся на единицу длины  , умноженный на длину элемента  , т.е.  , тогда  . Интегрируя по длине стержня, получим  .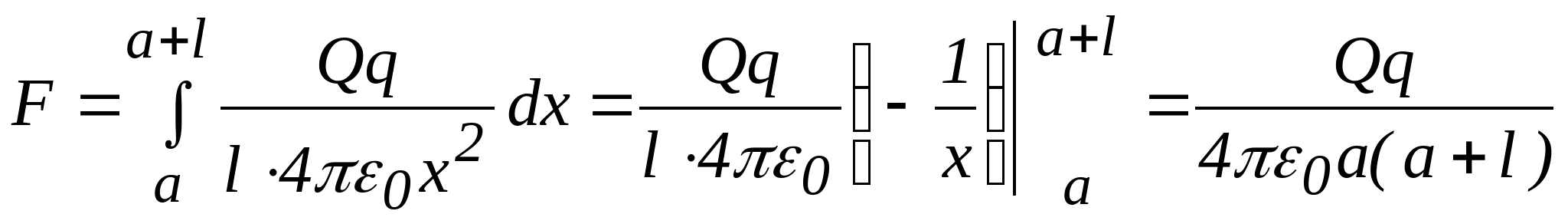

Заметим, что при  , т.е. стержень уже можно считать точечным зарядом.

Напряженность электрического поля – это его силовая характеристика, векторная величина, определяемая отношением силы, действующей на заряд в данной точке поля, к величине заряда.

Размерность  .

Концепция дальнодействия заключается в том, что при изменении положения одного заряда относительно другого заряда сила взаимодействия изменяется мгновенно.

Концепция близкодействия. При изменении положения одного заряда относительно другого сила взаимодействия изменяется с конечной скоростью (в вакууме – со скоростью света). Взаимодействие осуществляется при помощи посредника – электрического поля, создаваемого зарядами. Это концепция современной физики. Она пришла на смену концепции дальнодействия.

Принцип суперпозиции электрических полей. Как следует из опыта, сила, действующая на некоторый заряд со стороны системы зарядов, равна векторной сумме сил, с которыми каждый из зарядов системы действует на данный заряд  . Поделив последнее выражение на величину заряда, получим:  .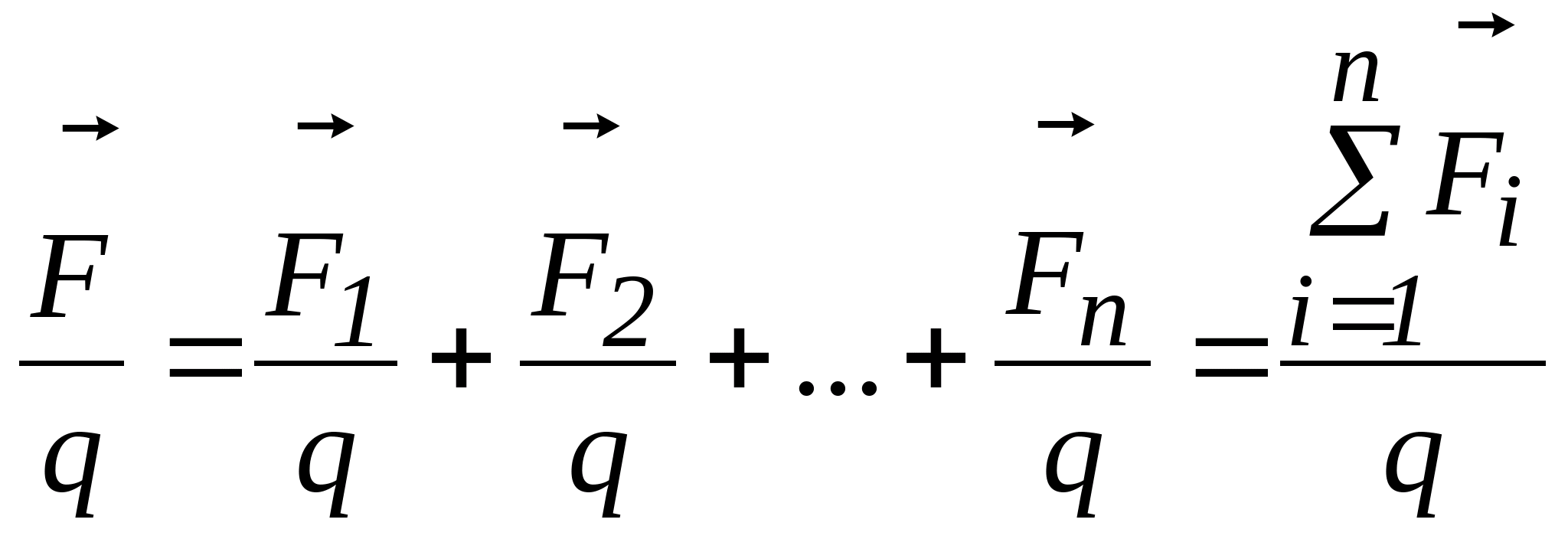

Из определения напряженности следует

Принцип суперпозиции электрических полей: напряженность поля, создаваемого системой зарядов в некоторой точке, равна векторной сумме напряженностей, создаваемых в отдельности каждым зарядом системы в данной точке.

Напряженность электрического поля, создаваемого точечным неподвижным зарядом в некоторой точке на расстоянии   от него, можно получить с помощью закона Кулона:

Силовые линии. Для наглядности электрические поля изображают с помощью силовых линий, т.е. воображаемых линий, в каждой точке которых напряженность   направлена по касательной. На рисунке 16.3 изображены картины силовых линий для некоторых случаев:

а)	б)	в)	г)
Рис. 16.3

а) и б) – одиночные заряды разных знаков,

в) система двух разноименных зарядов,

г) система двух одноименных зарядов.