Гармонические колебания

Деревянные игрушкиbanggood.com Скрыть рекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента Спасибо, объявление скрыто. Отделка балконовнедорого! Звони! pallet-okna.ru отделкаАдрес и телефонСкрыть рекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента Спасибо, объявление скрыто. Яндекс.Директ

Колебания и волны

 

Механические Колебания

 

Гармонические колебания.

 

Собственные (свободные колебания) – это колебания, которые совершает система, предоставленная самой себе после того, как она выведена из состояния равновесия.

Такие колебания могут быть незатухающими (в отсутствии трения) и затухающими.

Гармонические колебания – это колебания, происходящие по гармоническому закону. Под гармоническими функциями в математике понимают функции синуса и косинуса.

Осциллятор – тело, совершающее гармонические колебания.

Мы, в основном, будем использовать функцию косинуса.

Уравнение механических гармонических колебаний:

x– координата колеблющейся точки;

A = x_m – амплитуда колебаний;

w₀– угловая частота колебаний;

j₀– начальная фаза колебаний;

j = w₀t + j₀– фаза колебаний;

t– время.

Фаза колебаний – это СФВ, характеризующая состояние колебательной системы в данный момент времени, и равная аргументу, стоящему под знаком косинуса (синуса) в уравнении гармонических колебаний.

 – период колебаний;

 –частота колебаний.

Дадим другое определение гармонических колебаний.

Гармонические колебания – это колебания, происходящие под действием упругой (квазиупругой) силы, т.е. силы, подобной упругой и подчиняющейся формуле

 – квазиупругая сила

k– коэффициент упругости (квазиупругости)

 

 , 

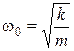
 – квазиупругая сила

 – дифференциальное уравнение (ДУ) гармонических колебаний.

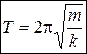 – период колебаний пружинного маятника

Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити.

Колебания математического маятника будут гармоническими только при малых углах отклонения (a < 5°).

 

 

Ox: 

 Þ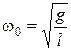 

 - период колебаний пружинного маятника (формула Гюйгенса)

Физический маятник – это твердое тело, способное совершать колебания вокруг неподвижной горизонтальной оси.

 

 

 

 

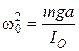
 – период колебаний физического маятника

Приведенная длина L физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

T_м = T_ф

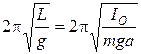 Þ 

 – полная энергия гармонических колебаний

 

Аналогии между механическими и электромагнитными колебаниями

Механические колебания	Электромагнитные колебания
Координата, x	Электрический заряд, q
Проекция скорости,	Сила тока,
Проекция ускорения,   ax	Скорость изменения тока,
Масса, m	Индуктивность, L
Коэффициент упругости, k	Величина, обратная электроемкости, 1/C
Угловая частота,	Угловая частота,
Потенциальная энергия,	Энергия электрического поля,
Кинетическая энергия,	Энергия магнитного поля,
Коэффициент сопротивления среды, r	Активное сопротивление, R
Внешняя сила, F	ЭДС и напряжение, ℰ и U

 

 – формула Томсона

ℰ_S = – u!

КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА

КОЛЕБАНИЯ

Лекция 1

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

Колебание – один из самых распространённых процессов в природе и технике. Колебания – это процессы, повторяющиеся во времени. Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведённых часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни. Звук – это колебания давления воздуха, радиоволны – периодические изменения напряжённости электрического и магнитного поля, свет – это тоже электромагнитные колебания. Землетрясения – колебания почвы, приливы и отливы – изменение уровней морей и океанов, вызываемые притяжением луны и т.д.

Колебания бывают механические, электромагнитные, химические, термодинамические и др. Несмотря на такое многообразие, все колебания описываются одними и теми же дифференциальными уравнениями.

Первыми учёными, изучавшими колебания, были Галилео Галилей и Христиан Гюйгенс. Галилей установил независимость периода колебаний от амплитуды. Гюйгенс изобрёл часы с маятником.

Любая система, которая, будучи слегка выведена из положения равновесия, совершает устойчивые колебания, называется гармоническим осциллятором. В классической физике такими системами являются математический маятник в пределах малых углов отклонения, груз в пределах малых амплитуд колебаний, электрический контур, состоящий из линейных элементов ёмкости и индуктивности.

Гармонический осциллятор можно считать линейным, если смещение от положения равновесия прямо пропорционально возмущающей силе. Частота колебаний гармонического осциллятора не зависит от амплитуды. Для осциллятора выполняется принцип суперпозиции - если действуют несколько возмущающих сил, то эффект их суммарного действия может быть получен как результат сложения эффектов от действующих сил в отдельности.

 Гармонические колебания описываются уравнением (рис.1.1.1)

 (1.1.1)

где х -смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, равная величине максимального смещения,   - фаза колебаний, определяющая смещение в момент времени   ,   - начальная фаза, определяющая величину смещения   в начальный момент времени,   - циклическая частота колебаний.

Время одного полного колебания называется периодом,   , где   - число колебаний, совершенных за время   .

Частота колебаний   определяет число колебаний, совершаемых в единицу времени, она связана с циклической частотой соотношением   , тогда период   .

Скорость колеблющейся материальной точки

 ,

ускорение

 . (1.1.2)

Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудами   и   соответственно. При этом скорость опережает по фазе смещение на   , а ускорение – на   (рис.1.1.2).

 Из сопоставления уравнений движения гармонического осциллятора (1.1.1) и (1.1.2) следует, что   , или

 . (1.1.3)

Это дифференциальное уравнение второго порядка называется уравнением гармонического осциллятора. Его решение содержит два постоянные а и   , которые определяются заданием начальных условий

 .

Отсюда   .

Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он н6азывается ангармоническим. Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.

 

1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний

В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.

Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия   имеет минимум (q – обобщённая координата системы). Отклонение системы от положения равновесия приводит к возникновению силы   , которая стремится вернуть систему обратно. Значение обобщённой координаты, соответствующей положению равновесия, обозначим   , тогда отклонение от положения равновесия 

Будем отсчитывать потенциальную энергию от минимального значения   . Примем   Полученную функцию   разложим в ряд Маклорена и оставим первый член разложения, имеем: о

 ,

где   . Тогда с учётом введённых обозначений:

 , (1.1.4)

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:

Согласно второму закону Ньютона, уравнение движения системы имеет вид:   ,

тогда

 , (1.1.5)

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

 , (1.1.6)

и имеет два независимых решения:   и   , так что общее решение:

 , или

 ,

где 

Из формулы (1.1.6) следует, что частота определяется только собственными свойствами механической системы и не зависит от амплитуды и от начальных условий движения.

Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения   , где A=Xe-iα– комплексная амплитуда, её модуль совпадает с обычной амплитудой, а аргумент – с начальной фазой.

 

1.1.3. Примеры колебательных движений различной физической природы

Колебания груза на пружине

Рассмотрим колебания груза на пружине, при условии, что пружина не деформирована за пределы упругости. Покажем, что такой груз будет совершать гармонические колебания относительно положения равновесия (рис.1.1.3). Действительно, согласно закону Гука, сжатая или растянутая пружина создаёт гармоническую силу:

где   – коэффициент жёсткости пружины,   – координата положения равновесия, х – координата груза (материальной точки) в момент времени   ,   - смещение от положения равновесия.

Поместим начало отсчета координаты в положение равновесия системы. В этом случае   .

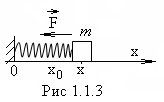 Если пружину растянуть на величину х, после чего отпустить в момент времени t=0, то уравнение движения груза согласно второму закону Ньютона примет вид -kx =ma, или   , и

 (1.1.6)

Это уравнение совпадает по виду с уравнением движения (1.1.3) системы, совершающей гармонические колебания, его решение будем искать в виде:

 . (1.1.7)

Подставим (1.17) в (1.1.6), имеем:   то есть выражение (1.1.7) является решением уравнения (1.1.6) при условии, что 

Если в начальный момент времени положение груза было произвольным, то уравнение движения примет вид:

 .

Рассмотрим, как меняется энергия груза, совершающего гармонические колебания в отсутствие внешних сил (рис.1.14). Если в момент времени t=0 грузу сообщить смещение х=А, то его полная энергия станет равной потенциальной энергии деформированной пружины   , кинетическая энергия равна нулю (точка 1).

 На груз действует сила F= -kx, стремящаяся вернуть его в положение равновесия, поэтому груз движется с ускорением и увеличивает свою скорость, а, следовательно, и кинетическую энергию. Эта сила сокращает смещение груза х, потенциальная энергия груза убывает, переходя в кинетическую. Система «груз - пружина» замкнутая, поэтому её полная энергия сохраняется, то есть:

 . (1.1.8)

В момент времени   груз находится в положении равновесия (точка 2), его потенциальная энергия равна нулю, а кинетическая максимальна   . Максимальную скорость груза найдём из закона сохранения энергии (1.1.8):

За счёт запаса кинетической энергии груз совершает работу против упругой силы –   и пролетает положение равновесия. Кинетическая энергия постепенно переходит в потенциальную. При   груз имеет максимальное отрицательное смещение –А, кинетическая энергия Wk=0, груз останавливается и начинает движение к положению равновесия под действием упругой силы F= -kx. Далее движение происходит аналогично.

 

Маятники

Под маятником понимают твёрдое тело, которое совершает под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятники.

Математический маятник – это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной материальной точке.

 Математическим маятником, например, является шарик на длинной тонкой нити.

Отклонение маятника от положения равновесия характеризуется углом φ, который образует нить с вертикалью (рис.1.15). При отклонении маятника от положения равновесия возникает момент внешних сил (силы тяжести)   :   , где m – масса,   – длина маятника

Этот момент стремится вернуть маятник в положение равновесия (аналогично квазиупругой силе) и направлен противоположно смещению φ, поэтому в формуле стоит знак «минус».

Уравнение динамики вращательного движения для маятника имеет вид: Iε=   ,

или

 .

Будем рассматривать случай малых колебаний, поэтому sin φ ≈φ, обозначим   ,

имеем:   , или   , и окончательно

 .

Это уравнение гармонических колебаний, его решение:

 .

Частота колебаний математического маятника определяется только его длиной и ускорением силы тяжести, и не зависит от массы маятника. Период равен:

 .

Если колеблющееся тело нельзя представить, как материальную точку, то маятник называют физическим (рис.1.1.6). Уравнение его движения запишем в виде:

   .

В случае малых колебаний   , или   =0 , где   . Это уравнение движения тела, совершающего гармонические колебания. Частота колебаний физического маятника зависит от его массы, длины и момента инерции относительно оси, проходящей через точку подвеса.

Обозначим   . Величина   называется приведённой длинной физического маятника. Это длина математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (О’). Если маятник подвесить в центре качания, то приведённая длина и период колебаний будут теми же, что и в точке О. Таким образом, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качения прежняя точка подвеса становится новым центром качения.

Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.