
- •Паспорт Уважаемые студенты!
- •Введение
- •Раздел 1. Теория пределов Тема 1.1. Понятие предела числовой последовательности
- •Тема 1.2. Понятие предела функции на бесконечности и в точке
- •Тема 1.3. Односторонние пределы
- •Теоремы о пределах
- •Замечательные пределы
- •Тема 1.4. Непрерывность функции
- •Задания для самоконтроля
- •Раздел 2. Дифференциальное исчисление Тема 2.1. Производная функции Определение функции
- •Геометрический смысл производной
- •Правила дифференцирования
- •Производная сложной функций
- •Производная обратной функции
- •Уравнение касательной к графику функции
- •Алгоритм составления уравнения касательной к графику функции
- •Тема 2.2. Исследование функции с помощью производной Экстремум функции и интервалы монотонности
- •Экстремум функции
- •Наибольшее и наименьшее значение функции на отрезке
- •Выпуклость функции. Точки перегиба
- •Задания для самоконтроля
- •Раздел 3. Интегральное исчисление Тема 3.1. Неопределенный интеграл Понятие первообразной, неопределенного интеграла
- •Свойства неопределенного интеграла.
- •Табличные интегралы
- •Методы вычисления неопределенных интегралов
- •Тема 3.2. Определенный интеграл
- •Свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Вычисление площади фигуры
- •Задания для самоконтроля
- •Раздел 4. Численные методы
- •4.1. Численное дифференцирование Особенность задачи численного дифференцирования
- •Численное дифференцирование на основе интерполяционной формулы Лагранжа
- •Численное дифференцирование на основе интерполяционной формулы Ньютона
- •4.2. Численное интегрирование Постановка задачи
- •Метод прямоугольников
- •Метод трапеций
- •Метод парабол (Симпсона)
- •Список литературы Основные источники:
- •Дополнительные источники:
- •Интернет-ресурсы:
- •Ответы на задания для самоконтроля
- •1. Вычислить пределы
- •Раздел 2. Дифференциальное исчисление
- •1. Вычислить производную функции:
- •Раздел 3. Интегральное исчисление
- •1.Вычислите неопределенные интегралы:
- •2. Вычислите определенные интегралы:
- •3. Вычислить площадь фигуры, ограниченной линиями:
- •Задание для итогового контроля
- •Тестовые задания
- •68. Дифференциал функции равен …
- •Эталон ответов на задание для итогового контроля
- •Практическое задание Рекомендации по выполнению практического задания
Тема 1.3. Односторонние пределы
В определении предела функции считается, что x стремится к х0 любым способом: оставаясь меньшим, чем х0 (слева от х0), большим, чем х0 (справа от х0), или колеблясь около точки х0.
Бывают случаи, когда способ приближения аргумента х к х0существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Определение:
Число А1
называется пределом функции у=f(x)
слева в точке х0,
если для любого число ε>0 существует
число =
(ε)>0, такое, что при
 ,
выполняется неравенство
,
выполняется неравенство
 .
.
Предел
слева записывается так:
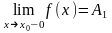 или f(x0
– 0)=A1.
или f(x0
– 0)=A1.
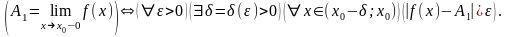
Аналогично определяется предел функции справа:
Определение:
Число А2
называется пределом функции у=f(x)
спарава в точке х0,
если для любого число ε>0 существует
число =
(ε)>0, такое, что при
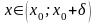 ,
выполняется неравенство
,
выполняется неравенство
 .
.
Предел
справа записывается так:
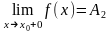 или f(x0
+ 0)=A2.
или f(x0
+ 0)=A2.

Теоремы о пределах
Если существуют пределы функций f(x) и g(x), то существует предел их суммы, равный сумме пределов функций f(x) и g(x)

Если существуют пределы функций f(x) и g(x), то существует предел их произведения, равный произведению пределов функций f(x) и g(x)
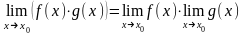
Если существуют пределы функций f(x) и g(x) и предел функции g(x) не равен нулю, то существует предел их отношения, равный отношению пределов функций f(x) и g(x)
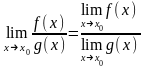
Следствие:
1)
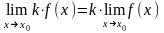
2)
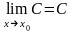
Замечание:

Пример1.
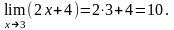
Пример2.
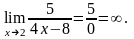
Пример3.
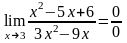 .
Получили неопределенность типа 0\0. Чтобы
от нее избавиться необходимо, преобразовать
числитель и знаменатель выражения.
Данные выражения представляют собой
квадратные многочлены, поэтому, пользуясь
формулой
.
Получили неопределенность типа 0\0. Чтобы
от нее избавиться необходимо, преобразовать
числитель и знаменатель выражения.
Данные выражения представляют собой
квадратные многочлены, поэтому, пользуясь
формулой
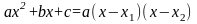 разложения квадратного многочлена на
множители, разложим на множители
числитель и знаменатель.
разложения квадратного многочлена на
множители, разложим на множители
числитель и знаменатель.
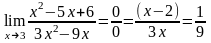
Замечание:
При решении примеров на нахождение
пределов не редко могут встретиться
неопределенности вида:

Для того, чтобы избавиться от таких неопределенностей выражение под знаком предела обычно преобразуют. Если выражение дробь, в числителе и в знаменатели которой находятся многочлены, то их раскладывают на множители. Если содержится выражение содержащее знак корня, то числитель и знаменатель домнажают на сопряженное число. Если выражение содержит разность или сумму дробей, то оно приводится к общему знаменателю.
Пример 4. Вычислить:
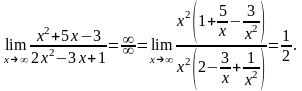
При решении воспользовались формулой

Замечательные пределы
Первый замечательный предел
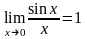
Следствие:
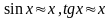
Второй замечательный предел
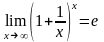 или
или

Пример 5.
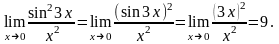
Пример 6.

Тема 1.4. Непрерывность функции
Понятие непрерывности функции, так же как и понятие предела, является одним из основных понятий математического анализа.
Определение. Функция f(х) называется непрерывной в точке x0, если она удовлетворяет следующим трем условиям:
1) определена в точке x0 (т.е. существует f(х0));
2) имеет конечный предел функции при х →х0;
3) этот предел равен значению функции в точке х0, т.е.

Пример
7.
Исследовать непрерывность в точке х
= 0 заданной функции:
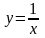 .
.
Решение:
а) В точке x=0 y=f(x) не является непрерывной, так как нарушено первое условие непрерывности – существование f(0).
 Рисунок
3 – График функции
Рисунок
3 – График функции
Функция f(x) непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.
Точка х0 называется точкой разрыва функции f(х), если эта функция в данной точке не является непрерывной. Различают точки разрыва:
первого рода (когда существуют конечные односторонние пределы функции слева и справа при х →х0, не равные друг другу);
Если
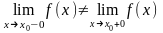 ,
то х0 – точка разрыва I
рода.
,
то х0 – точка разрыва I
рода.
второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует).
Если
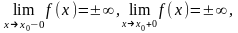 то точка х0– точка разрыва II
рода.
то точка х0– точка разрыва II
рода.
устранимого разрыва, когда предел функции при х →х0 существует, но не равен значению функции в этой точке.
Если
 то в точке х0 – устранимый
разрыв.
то в точке х0 – устранимый
разрыв.
Нахождение асимптот
Асимптотой графика функции у = f(x) – называется прямая, обладающая тем свойством, что расстояние от точки до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Асимптоты бывают: наклонные, горизонтальные, вертикальные.
Уравнение наклонной асимптоты находим
в виде у=kх+b,
где
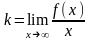 ,
,
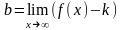 .
.
Пример 8. Исследовать график функции
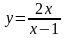 в точках х=1, х=2 и выполнить
построение.
в точках х=1, х=2 и выполнить
построение.
1) х=1 вертикальная асимптота, т.к. х=1 – точка разрыва (на нуль делить нельзя).
2) Определим вид разрыва в точке х=1
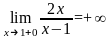 и
и
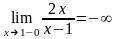 следовательно х=1 точка разрыва II
рода.
следовательно х=1 точка разрыва II
рода.
3) Находим наклонные асимптоты из уравнения у=kх +b
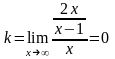 и
и
 итак у=1 – горизонтальная асимптота.
итак у=1 – горизонтальная асимптота.
4) Исследуем поведение функции в точке х=2
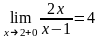 и
и
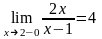 ,
и f(2)=4 т.к. выполнены
условия непрерывности функции в точке,
функция в т. х=2 является непрерывной.
,
и f(2)=4 т.к. выполнены
условия непрерывности функции в точке,
функция в т. х=2 является непрерывной.
Построение:
На координатной прямой изобразили найденные асимптоты.
Обратили внимание на поведение функции справа и слева от точки разрыва.
При х=0 у=0 использовали уточняющее условие, для построения графика.

Рисунок 4 – График функции
