Устойчивость

Во временной области цифровой фильтр устойчив, если его импульсная характеристика удовлетворяет условию (11.18). Теперь определим условия устойчивости цифровых фильтров в  -области.

Для этого рассмотрим общую передаточную функцию, заданную выражением (11.40), которое для удобства приведено еще раз:

Любой фильтр с передаточными функциями вида (11.163) при   называется цифровым фильтром с бесконечной импульсной характеристикой   поскольку не существует конечного целого числа   такого, что

где   — импульсная характеристика фильтра. Для цифровых   фильтров положим, что

Это предположение верно почти для всех практических случаев. Разложение уравнения (11.163) на простые дроби дает

где

Следовательно, импульсная характеристика, соответствующая выражению (11.163), определяется следующим соотношением:

Ясно, что необходимые и достаточные условия того, что импульсная характеристика, заданная выражением (11.167), удовлетворяет критерию устойчивости

имеют вид  .

Это означает, что все полюсы цифрового фильтра расположены внутри единичного круга в z-плоскости.

Рис. 11.15. Устойчивая цифровая схема к примеру 11.20.

Пример 11.20. Показать, что схема, приведенная на рис. 11.15, устойчива. Решение. Разностное уравнение, описывающее эту схему, равно

Передаточную функцию схемы можно получить, применив  -преобразование к соотношению (11.170):

Следовательно, полюсы фильтра расположены в точках

Таким образом, функцию   можно переписать в виде

Поскольку

схема на рис. 11.15 устойчива

Если передаточная функция цифрового фильтра представлена в виде

что эквивалентно случаю   в выражении (11.163), то цифровой фильтр называют фильтром с конечной импульсной характеристикой (КИХ). Это обозначение используют вследствие того, что импульсная характеристика, соответствующая уравнению (11.175), удовлетворяет следующему условию:

Таким образом, соответствующая импульсная характеристика имеет конечную протяженность. В этом случае отсутствуют полюсы, и поэтому этот тип фильтра всегда устойчив.

Структуры цифровых фильтров и их характеристики

мы рассмотрели разностные уравнения цифровых фильтров в виде:

(1)

где   - отсчеты на выходе фильтра,   - входные отсчеты,   и   - коэффициенты числителя и знаменателя передаточной характеристики фильтра соответственно. Также мы говорили о том, что если все коэффициенты  кроме   равны нулю, то такой фильтр называется КИХ-фильтром, а если хотя бы один коэффициент   помимо  отличен от нуля, то такой фильтр называется БИХ-фильтр.

В данной статье мы рассмотрим структурные схемы цифровых фильтров и их характеристики.

Основные обозначения

Согласно выражению (1), сигнал на выходе фильтра зависит от задержанного входного сигнала, а также от предыдущих отсчетов на выходе, поэтому для реализации фильтра нам потребуются линии задержки. Вспомним, что согласно z-преобразованию, задержка на один отсчет соответствует умножению образа на  . Также нам потребуются умножители на постоянные коэффициенты   и   и сумматоры. На рисунке 1 показаны обозначения основных блоков для построения цифрового фильтра.

Рисунок 1: Обозначения блоков цифрового фильтра

На рисунке 1 а) обозначена линия задержки, 1 б) умножитель на константу, 1 в) сумматор и 1 г) разветвление.

Структурная схема КИХ-фильтра

Разностное уравнение КИХ фильтра не содержит рекурсивной части:

(2)

Выражение (2) получается из выражения (1) при   и  .

Структурная схема нерекурсивного КИХ-фильтра показана на рисунке 2.

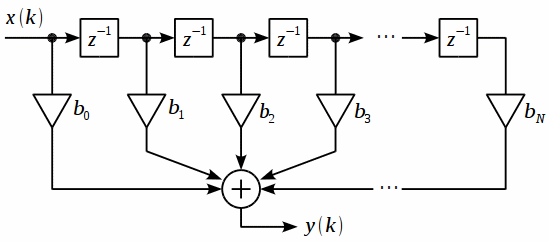Рисунок 2: Структурная схема нерекурсивного КИХ-фильтра

КИХ фильтр порядка   содержит   линий задержки и   коэффициент. Если коэффициент  , то получим КИХ фильтр порядка   у которого умножение на   будет тривиальным. Импульсная характеристика КИХ-фильтра всегда конечна и полностью совпадает с коэффициентами фильтра.

Структурные схемы БИХ-фильтра. Прямая и каноническая формы БИХ-фильтра

При построении БИХ-фильтра перепишем уравнение (1) к виду:

(3)

В выражении (3) можно выделить нерекурсивную составляющую   и рекурсивную  . Тогда БИХ-фильтр можно представить как сумму нерекурсивной и рекурсивной составляющих, как это показано на рисунке 3.

Рисунок 3: Прямая форма БИХ-фильтра

Такое представление БИХ-фильтра называют прямой формой реализации. Обратим внимание, что количество линий задержек БИХ-фильтра равно  , что больше чем количество линий задержек КИХ-фильтра того же порядка (напомним, что порядок БИХ-фильтра равен максимальной степени полинома числителя или знаменателя передаточной характеристики фильтра). При этом также обратим внимание, что БИХ фильтр представляет собой каскадное соединение нерекурсивной и рекурсивной частей, которые можно поменять местами. Тогда получим структуру, показанную на рисунке 4.

Рисунок 4: Перестановка нерекурсивной и рекурсивной составляющих БИХ-фильтра

Объединив линии задержки в структуре, показанной на рисунке 4, получим каноническую форму БИХ-фильтра, представленную на рисунке 5.

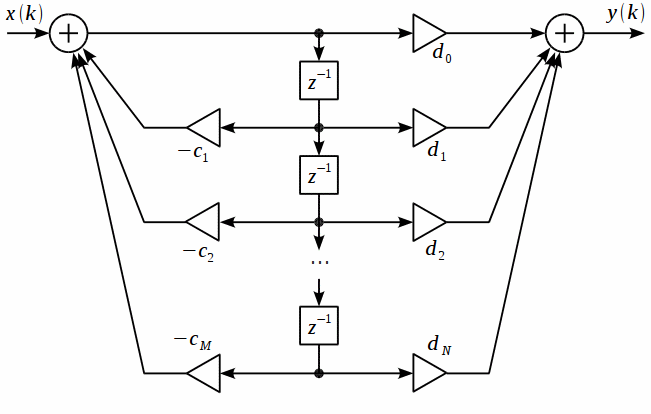Рисунок 5: Каноническая форма БИХ-фильтра

В канонической форме БИХ-фильтра количество линий задержек всегда равно порядку фильтра.

Характеристики цифровых фильтров

Ранее мы уже говорили, что цифровой фильтр задается свой передаточной характеристикой  , которая представляет отношение z-образов   выходного сигнала ко входному  :

(4)

При этом мы уже знаем, что z-преобразование мы получили путем отображения комплексной s-плоскости вида  где   - период дискретизации исходного сигнала и импульсной характеристики фильтра. Без потери общности можно принять  , тогда   Тогда подставив в передаточную характеристику дискретного фильтра (4)  , мы получим передаточную характеристику фильтра по Лапласу, из которой можно получить комплексный коэффициент передачи дискретного фильтра путем подстановки  . Таким образом, комплексный коэффициент передачи цифрового фильтра обозначается как   и равен:

(5)

Амплитудно-частотная характеристика (АЧХ) цифрового фильтра может быть получена как модуль  , а фазочастотная (ФЧХ) как аргумент:

(6)

Также вводят понятие групповой задержки как производной от ФЧХ:

(7)

Обратите внимание, что АЧХ и ФЧХ и групповая задержка цифрового фильтра есть непрерывные функции частоты. При этом согласно (5)   периодическая функция с периодом  , так как  . Последнее равенство не вызывает сомнений, если подставить его в выражение (5). Таким образом, характеристику цифрового фильтра достаточно проанализировать на интервале  .

Цифровой фильтр также определяется своей импульсной характеристикой, преобразование Фурье от которой дает комплексный коэффициент передачи. Если комплексный коэффициент передачи — периодическая функция частоты, то импульсная характеристика   дискретного фильтра определяется как разложение в ряд Фурье  :

.

(8)

Рассчитывать импульсную характеристику через интеграл не совсем удобно, кроме того количество отсчетов импульсной характеристики   БИХ-фильтра бесконечно, и все их рассчитать невозможно. Однако, если фильтр устойчивый, то   убывает, с увеличением  , и можно рассчитать заданное количество отсчетов импульсной характеристики фильтра при помощи быстрого преобразования Фурье (FFT).

Пусть требуется рассчитать   первых отсчетов импульсной характеристики фильтра, заданного передаточной характеристикой 

Первое, что мы должны сделать — рассчитать комплексный коэффициент передачи заданного фильтра. Для численного расчета необходимо задать сетку частот      . Тогда на данной сетке частот рассчитаем комплексный коэффициент передачи  , таким образом, получим   отсчетов комплексного коэффициента передачи фильтра. После этого можно рассчитать импульсную характеристику как  ,  где   - оператор обратного быстрого преобразования Фурье. Таким образом, мы рассчитали характеристики фильтра с заданной передаточной характеристикой. Данный путь расчета приводил к комплексному коэффициенту передачи в частотной области, с последующим преобразованием во временную.

На рисунках 6 и 7 показаны рассчитанные характеристики фильтра при   и

.

(9)

Рисунок 6: Импульсная характеристика фильтра

Рисунок 7: Один период АЧХ и ФЧХ фильтра

Обратите внимание, что на рисунке 7 по оси абсцисс показана частота  , таким образом, АЧХ и ФЧХ представлена для нормированных частот от 0 до 2. Кроме того, можно заметить, что АЧХ фильтра   является симметричной относительно частоты  , или  , т.е.  , а ФЧХ является антисимметричной, т.е.  .

Рассмотрим теперь другой способ расчета характеристик фильтра — расчет во временной области. Для этого приведем структурную схему фильтра, заданного передаточной характеристикой (9) (рисунок 8).

Рисунок 8: Структурная схема фильтра

Для того, чтобы получить импульсную характеристику цифрового фильтра, необходимо подать на вход сигнал :

(10)

Тогда на выходе фильтра будет импульсная характеристика. Рассчитаем импульсную характеристику на выходе фильтра по его структуре.

Пусть на входе нулевой отсчет  , тогда точка «а» равна 1, «б» и «в» равна нулю, тогда на выходе . При поступлении на вход отсчета   получим точка «б» равна 1 (задержанная точка «a»), точка «в» равна 0.7 и точка «а» при   равна 0.7, тогда  . При   имеем: , точка «б» равна 0.7, тогда точка «в» равна  , точка «а» равна 0.49 и . Так можно продолжать до бесконечности. Ограничившись как и в предыдущем случае  отсчетами импульсной характеристики получим   полностью совпадающую с приведенной на рисунке выше. Тогда комплексный коэффициент передачи фильтра можно получить если взять БПФ от импульсной характеристики .

Оба приведенных способа расчета характеристик фильтра имеют приблизительно одну вычислительную сложность и какой из них выбрать решать пользователю