6.6. Точки разрыва функции и их классификация

Определение 6.7. Точка называется точкой разрыва функции , если точка принадлежит области определения функции или её границе и не является точкой непрерывности функции.

В этом случае говорят, что при функция разрывна. Такая ситуация возникает, если в точке x₀ функция не определена или не существует предел , или если предел существует, но .

Классификации точек разрыва

Обычно у функций, встречающихся в математике, точки разрыва изолированы, но существуют функции, для которых все точки являются точками разрыва, например функция Дирихле, определенная следующим образом:

f (x) = 0, если х рационально, и f (x) = 1, если х иррационально.

В дальнейшем будем рассматривать изолированные точки разрыва, т.е такие, в окрестности которых нет других точек разрыва. Точки разрыва бывают двух типов.

Для рассмотрим предел слева и предел справа функции f(x). Тогда имеет место следующая классификация точек разрыва.

Определение 6.8. Точка называется точкой разрыва 1 рода (устранимый разрыв) функции , если (см. рис. 6.1) точка принадлежит области определения функции, существуют оба односторонних предела: 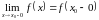и , но при этом .

В данном случае достаточно изменить значение функции в точке x₀, чтобы разрыва не стало.

Рис. 6.1 Вид устранимого разрыва

Определение 6.9. Точка называется точкой разрыва 1 рода (скачок) функции , если (см. рис. 6.2) точка принадлежит области определения функции, существуют и конечны оба односторонних предела: и , но при этом они не равны между собой: . В этом случае не существует .

Рисунок 6.2. Изображение функции, имеющей разрыв 1-ого рода (скачок)

Определение 6.10. Точка называется точкой разрыва 2 рода (бесконечный разрыв) функции , если (см. рис. 6.3) точка не принадлежит области определения функции, или хотя бы один из двух пределов или 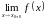равен бесконечности.

Рисунок 6.3. Пример разрыва второго рода

П римеры.

1. Рассмотрим функцию (см. рис. 6.4):

Рисунок 6.4. Изображение разрыва 1 рода (скачок)

Эта функция определена во всех точках отрезка [0, 4] и её значение при x = 3 равно 0. Однако, в точке x = 3 функция имеет разрыв, т.к. она не имеет предела при x = 3:

Вывод: точка х = 3 – точка разрыва 1-ого рода (скачок).

2. Функция – разрывна при x = 0. Действительно, предел слева: 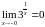, предел справа . . При x = 0 функция не определена. В точке x = 0 функция разрыв второго рода

6.7. Асимптоты графика функции

Определение 6.11. Асимптотой графика функции называется прямая, к которой стремится график функции при бесконечном удалении от начала координат, т.е. расстояние от прямой, называемой асимптотой и графиком функции стремится к нулю.

Асимптоты бывают вертикальные, горизонтальные и наклонные.

Определение 6.12. Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или или равно или .

Можно говорить о правосторонних и левосторонних вертикальных асимптотах, если рассматривать соответствующие пределы отдельно при или при .

Определение 6.13. . Прямая называется наклонной асимптотой к графику функции , если при функция может быть представлена в виде: , где функция является бесконечно малой при .

Теорема 6.12. Для того чтобы график функции имел наклонную асимптоту , необходимо и достаточно, чтобы существовали два конечных предельных значения: и .

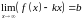Доказательство. Необходимость. Пусть график функции имеет наклонную асимптоту: , т.е. , где функция является бесконечно малой при . Рассмотрим , т.к. и .

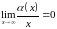Другой предел .

Таким образом, получили формулы для нахождения параметров и наклонной асимптоты.

Достаточность. Пусть существуют два конечных предельных значения: и . Из второй формулы следует, что , где функция является бесконечно малой при . Таким образом, , что означает, что прямая является наклонной асимптотой графика функции .

Теорема доказана.

Определение 6.14. Прямая называется горизонтальной асимптотой к графику функции , если существует конечный предел , т.е. угловой коэффициент наклона в уравнении наклонной асимптоты .

Можно говорить о правосторонних и левосторонних наклонных или горизонтальных асимптотах, если рассматривать соответствующие пределы отдельно при или при .

Часто график функции может иметь асимптоты различных видов. На рисунке 6.5 видно, что функция имеет вертикальную асимптоту: и наклонную асимптоту: .

Рисунок 6.5. Изображение наклонной и вертикальной асимптот

На рисунке 6.6 видно, что функция имеет вертикальную асимптоту: и горизонтальную асимптоту .

Рисунок 6.6. Изображение вертикальной и горизонтальной асимптот

16