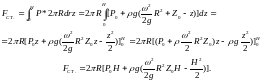4.6. Расположение свободной поверхности в сосуде

Рис.4.8. Три случая относительного покоя при вращении

1. Если сосуд открыт, Po=Ратм (рис.4.8а). Вершина параболоида при вращении опускается ниже начального уровня-Н, а края поднимаются над начальным уровнем, положение вершины

2. Если сосуд заполнен полностью, прикрыт крышкой, не имеет свободной поверхности, находится под избыточным давлением Ро>Ратм, до вращения поверхность (П.П.), на которой Ро=Ратм будет находиться над уровнем крышки на высоте h_0и=М/ρg , H₁=Н+ М/ρg.

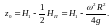
3. Если сосуд заполнен полностью, находится под вакуумом Ро<Ратм, до вращения поверхность П.П., на которой Ро=Ратм будет находиться под уровнем крышки на высоте h_0и=-V/ρg, Н₂=Н-V/ρg ,

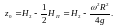
4.7. Вращение с большой угловой скоростью (рис.4.9)

При вращении сосуда с жидкостью с большой угловой скоростью силой тяжести можно пренебречь по сравнению с центробежными силами. Закон изменения давления в жидкости можно получить из формулы

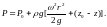(4.22),

Поверхности уровня образуют цилиндры с общей осью, вокруг которой вращается сосуд. Если сосуд перед началом вращения не полностью заполнен, давление Р₀ будет действовать не в центре, а при r = r₀, вместо выражения (4.22) будем иметь

в которой принимаем g(z₀ - z) = 0,

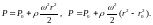
Рис. 4.9 Расположение поверхностей вращения при отсутствии силы тяжести.

Радиус внутренней поверхности

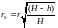
4.8 Определение силы давления жидкости на стенку, дно или крышку

Оси координат выбираем наиболее удобным образом на рис.4.10 ось Z - ось вращения, ось r - по поверхности крышки.

Для определения силы давления жидкости на дно или крышку выражаем силу, действующую на элементарную кольцевую площадку dS = 2πrdr радиусом r и шириной dr. Давление в любой точке ось r выбрана по верхней крышке:

Рис.4.10. Определение сил на крышку и дно сосуда(а).Эпюры давлений на крышку, стенку и дно сосуда(б). 1,2,3 – возможное расположение свободной поверхности параболоида относительно крышки.

При определении сил давления на крышку Z=0, возможны следующие варианты расположения параболоида

1) Z₀₁ > 0:

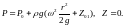
2)Z₀₂ =0:

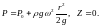
3) Z₀₃ < 0:

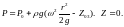
Для первого варианта. Выражение для силы dF, действующей на элементарную кольцевую площадку 2πrdr

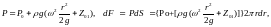
а затем выполняем интегрирование в требуемых пределах.

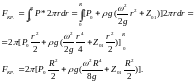
Также выполняется интегрирование во втором и третьем случае.

Определение сил давления жидкости на вертикальную стенку, сначала находим элементарную силу давления на кольцо, меняется высота, радиус остается неизменным

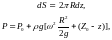
Сила, действующая на всю стенку равна