Построение сднф и скнф по таблице истинности. Правило построения скнф по таблице истинности.
Для каждого набора переменных, при котором функция равна нулю, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием. Далее, образуем конъюнкции всех полученных дизъюнкций.
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Решение.
Воспользуемся
правилом построения СКНФ. Имеется три
набора на которых функция равна
0: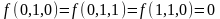
(третья,
четвертая, седьмая строки в таблице),
далее записываем сумму (дизъюнкцию)
переменных
,
причем переменные, которые имеют значение
1 берутся с отрицанием:
.Записывая
конъюнкции данных элементарных дизъюнкций
получим СКНФ:
.
Правило построения сднф по таблице истинности.
Для каждого набора переменных, при котором функция равна единицы, записывается произведение (конъюнкция), причем переменные, которые имеют значение 0,берутся с отрицанием. Далее, образуем дизъюнкции всех полученных конъюнкций.
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Решение.
Воспользуемся
правилом построения СДНФ. Для каждого
набора на которых функция равна 1:
,
записываем конъюнкции переменных
,
причем переменные ,которые имеют значение
0 берутся с отрицанием:
.
Записывая
дизъюнкции данных элементарных
конъюнкций, получим СДНФ:
Пример 3.21. Привести функцию заданную таблицей истинности к: а) СДНФ; б) СКНФ.
-
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
1
1
0
1
0
1
Решение.
а)
Выписываем наборы, где функция истинна
,
составляем по ним элементарные конъюнкции
образуя
дизъюнкции всех полученных конъюнкций,
получим
СДНФ:
.
б)
Выписываем ложные значения функции
,составляем
по данным наборам элементарные
дизъюнкции
образуем
конъюнкции
данных дизъюнкций, получаем
СКНФ:
.
Пример 3.22. Запишите формулу двумя способами ( с помощью равносильных преобразований и с помощью таблицы истинности) в виде: а) СДНФ; б) СКНФ.
Решение.
а)1 способ:
Используя равносильные преобразования и законы логики, приведем данную формулу к ДНФ, а затем к СДНФ:
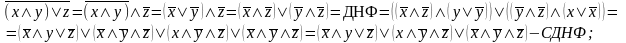2
способ:
Для построения СДНФ составим таблицу истинности для данной формулы:
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Отметим
те строки таблицы, в которых формула
(последний столбец) принимает значение
1:
составляем по ним элементарные конъюнкции,
причем переменные ,которые имеют значение
0 берутся с отрицанием
:
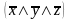-1 строка,
-3
строка,
-5
строка .Составляем дизъюнкции этих
конъюнкции получим совершенную
дизъюнктивную нормальную форму (СДНФ):
;
б) 1 способ:
Приведем данную формулу к КНФ, а затем к СКНФ:
2 способ:
Отметим
те строки таблицы (выше) в которых
формула принимает значение 0:
.
Для каждой такой строки выпишем формулу,
ложную на наборе переменных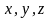 
:
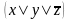-2
строка,
-4
строка,
-6
строка,
-7
строка,
-8
строка.
Составляя
конъюнкции
этих дизъюнкций, получим СКНФ :
Пример
3.23. Для
эквиваленции
,
при помощью таблицы истинности, написать:
а) СДНФ ; б)СКНФ.
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
а)Запишем
соответствующую таблицу истинности и
выпишем наборы, где функция истинна
,
составляем по ним элементарные конъюнкции
,таким образом СДНФ имеет вид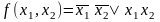
;
б)
Выписываем ложные значения функции
,
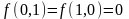составляем по данным наборам элементарные
дизъюнкции
,
,составляя их конъюнкции
-
СКНФ.
Формулы, содержащие кроме переменных и скобок только знаки операций дизъюнкции, конъюнкции и отрицания, называются булевыми формулами.
Таким образом, веденные СДНФ и СКНФ, являются булевыми формулами. Всякая логическая функция может быть представлена булевой формулой.
Под булевой алгеброй понимается алгебра, в которой логические операции состоят только из дизъюнкции, конъюнкции и отрицания.