Порядок выполнения работы

1. Запустить программу CLASSIC.bat из раздела UZER.

2. Вызвать главное меню {F10}. В разделе "Файл/Модель" выбрать режим работы "Ввод/Редактирование". Сформировать структуру САУ, состоящую из двух последовательно соединенных звеньев – формирователя задающего воздействия и исследуемого звена. Передаточные функции звеньев задать в виде и .

Указание: передаточные функции звеньев (клавиша {TAB}) задавать и редактировать путем ввода коэффициентов при степенях "s", начиная с нулевой. Переход к следующему коэффициенту производится нажатием клавиш {PGUP}, {PGDN}. Для управления типом задающего воздействия можно изменять параметры первого звена (идеальный усилитель или интегратор).

3. Сохранить схему САУ (режим "Запись в файл") с индивидуальным именем. Ознакомиться с возможностями режима "Анализ" раздела "Расчеты". Выполнить анализ и определить характерные точки полученных характеристик (вход в меню {F10}, режим "Значения"). Далее назначить исследуемое звено варьируемым и оценить влияние коэффициента усиления и постоянной времени на характеристики апериодического звена.

Определить соотношение длительности переходного процесса и характерных значений частотных характеристик САУ.

4. Исследовать характеристики апериодического звена второго порядка с передаточной функцией . Принять , и вариацией параметра получить различные виды переходного процесса, в том числе колебательный. Установить количественную связь величины выброса переходного процесса и параметра затухания .

5. Повторить эксперимент для линейно изменяющегося задающего воздействия.

6. Исследовать характеристики интегрирующих звеньев:

• Идеального интегратора, с передаточной функцией ;

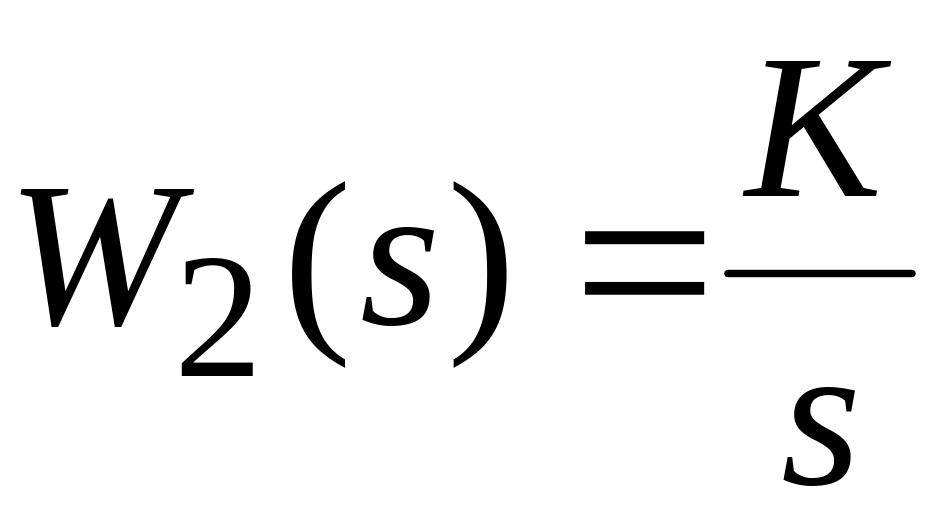• Инерционного, с передаточной функцией ;

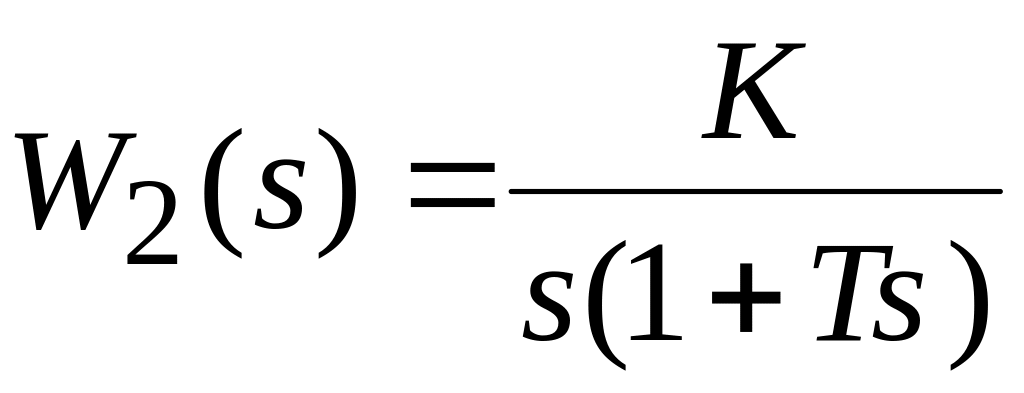• пропорционально интегрирующего (ПИ) звена, с передаточной функцией .

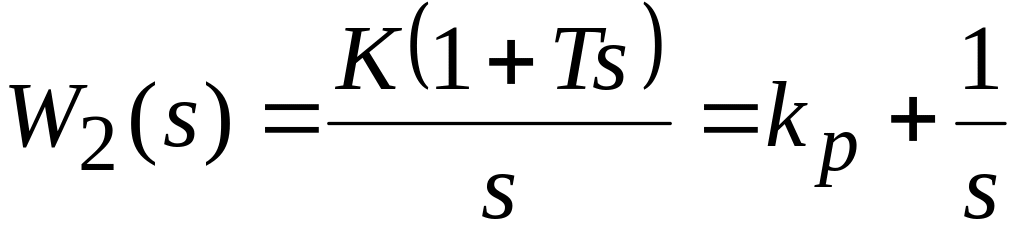Оценить степень влияния параметров и на характеристики звеньев.

7. Исследовать характеристики дифференцирующих звеньев:

• инерционного дифференцирующего, с ;

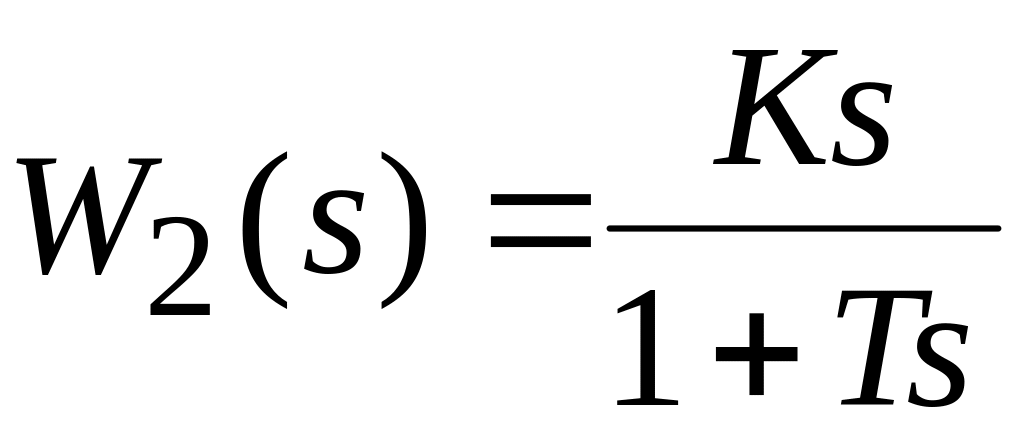– пропорционально-дифференцирующего (ПД или форсирующего), с передаточной функцией .

Оценить степень влияния инерционности на характеристики звена.

Содержание отчета

Графики переходных процессов.

Передаточные функции разомкнутых САУ.

Логарифмические частотные характеристики разомкнутых САУ.

Значения характерных частот и соответствующие им длительности переходных процессов.

Выводы о взаимосвязи частотных характеристик и качества переходного процесса.

Лабораторная работа №2

ИССЛЕДОВАНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СТАТИЧЕСКИХ САУ

Статическая САУ может содержать последовательно соединенные типовые звенья различного типа за исключением интеграторов. Передаточная функция разомкнутой САУ представлена в виде , где – общий коэффициент усиления, полиномы и имеют свободный член равный единице. Учет действия местных обратных связей (см. рис 2.3) производим в соответствии с выражением 1.1.

При охвате разомкнутой САУ единичной отрицательной обратной связью (главная обратная связь) передачу задающего воздействия на выход описывает главная передаточная функция .

Критерий Михайлова [Л.1] позволяет убедиться в устойчивости замкнутой САУ. Необходимым условием является положительность коэффициентов полинома . Достаточное условие устойчивости сводится к требованию последовательного прохождения кривой числа квадрантов, соответствующего порядку системы.

Для анализа ошибки по задающему воздействию вводят передаточную функцию ошибки, определяемую отношением преобразованных по Лапласу величин и . Используя очевидные соотношения и , получаем .

Установившуюся ошибку можно определить по изображению ошибки, воспользовавшись теоремой о конечном значении [Л.1], известной из теории преобразования Лапласа. Ошибка установившегося режима при отработке задающего воздействия называется статической. Для определения статической ошибки достаточно вычислить предел выражения при . После завершения переходного процесса статическая ошибка в любой замкнутой статической системе составляет .

Ошибка установившегося режима при отработке задающего воздействия, пропорционального постоянной скорости определяется тем же способом. Предел расходится, что указывает на неограниченное возрастание ошибки.

Динамическая ошибка определяется разностью мгновенных значений задающего воздействия и выходной координаты. Это позволяет оценивать ее по форме сигнала ошибки при простейших полиномиальных воздействиях. Для сложных передаточных функций целесообразно выполнить расчет в Mathcad. Задав изображение ошибки в форме для конкретной передаточной функции и вида входного воздействия, нужно выполнить обратное преобразование Лапласа.

Оценка качества процесса управления в замкнутой системе заключается в определении установившейся ошибки и некоторых параметров переходного процесса. Время установления определяют по уровню 5% отклонения от установившегося значения. Выброс (перерегулирование) измеряют в процентах от установившегося значения и обозначают %. Допустимое число колебаний обычно не превышает двух, а иногда колебания вообще недопустимы. Длительность фронта нарастания переходного процесса по уровню от 10 до 90% установившегося значения связана с частотой среза приближенным соотношением .

Весьма эффективны частотные методы оценки качества переходного процесса. Определим показатель колебательности как отношение максимального значения АЧХ замкнутой системы к значению АЧХ на нулевой частоте. Взаимосвязь между показателем колебательности и параметрами переходного процесса очевидна из анализа характеристик колебательного звена.

Принято считать [Л.2], что допустимый диапазон значений составляет от 1.1 до 1.5. Наиболее удобно представить результаты сопоставления в виде таблицы соответствия , которую нетрудно получить путем компьютерного моделирования.

Аналогичные результаты можно получить с использованием частотных характеристик разомкнутой системы. Критерий устойчивости Найквиста [Л.1] вводит понятия запаса по амплитуде и запаса по фазе . Их величины определяют по АФХ разомкнутой системы, либо по ее ЛЧХ. Запас по амплитуде равен расстоянию от точки пересечения АФХ с осью абсцисс до точки с координатами . Запас по фазе находят в точке, где . Эту частоту называют частотой среза . Запас по фазе равен углу между направлением вектора и отрицательной частью вещественной оси. В хорошо демпфированных системах 0.6, .

Как правило, используют логарифмические ЧХ. Запас по фазе определяют по ФЧХ , а запас по амплитуде соответствует частоте, на которой . В этом случае таблица соответствия связывает величину запаса по фазе , а запас по амплитуде имеет второстепенное значение.

Заметим, что на практике величину перерегулирования выбирают в диапазоне от 15 до 30%, а количество периодов колебаний не более одного или двух. Такой тип переходного процесса соответствует значениям параметра колебательности , либо запасу по фазе .

Порядок выполнения работы

1. Сформировать структурную схему САУ, состоящую из трех апериодических звеньев первого порядка, охваченных главной обратной связью. Передаточные функции звеньев задать в форме , , . Исследовать характеристики переходного процесса в замкнутой САУ при изменении параметров передаточной функции второго звена.

Определить длительность переходного процесса, величину перерегулирования (значение выброса в процентах от установившегося значения), период колебаний. По ЛЧХ определить показатель колебательности и полосу пропускания замкнутой системы. Измерить величину установившейся ошибки.

Коэффициент усиления варьировать в пределах 1…50 (рекомендуемый ряд значений 1, 2, 5, 10, 20) при неизменной постоянной времени звена.

Постоянную времени варьировать от 0.01 до 0.5 (рекомендуемый ряд значений 0.01, 0.1, 0.5) при фиксированном коэффициенте усиления .

2. Разомкнуть отрицательную обратную связь. Для тех же значений коэффициента усиления и постоянной времени второго звена по ЛЧХ измерить значение частоты единичного усиления разомкнутой САУ и величину запаса по фазе.

3. Сформировать структуру замкнутой системы, состоящей из апериодического звена первого порядка и колебательного звена с передаточными функциями и . Для колебательного звена коэффициенты соответствует параметру затухания и постоянной времени .

Исследовать характеристики переходного процесса в замкнутой САУ.

Определить длительность переходного процесса, величину перерегулирования (значение выброса в процентах от установившегося значения), период колебаний.

По ЛЧХ определить показатель колебательности и полосу пропускания замкнутой системы. Измерить величину установившейся ошибки.

Коэффициент усиления варьировать в пределах 1…20 (рекомендуемый ряд значений 1, 5, 20) при фиксированной величине . Величину параметра затухания ξ варьировать от 0.5 до 2 (рекомендуемый ряд значений 0.5, 0.707, 1, 2) при фиксированном коэффициенте усиления .

4. Разомкнуть отрицательную обратную связь. Для тех же значений коэффициента усиления и параметра затухания по ЛЧХ измерить значение частоты единичного усиления разомкнутой САУ и величину запаса по фазе.

5. Замкнуть отрицательную обратную связь. Качественно оценить влияние постоянной времени апериодического звена на характер переходного процесса. Постоянную времени варьировать от 0.01 до 20 (рекомендуемый ряд значений 0.01, 0.05, 0.1, 0.15, 10, 20) при фиксированном коэффициенте усиления.

Разомкнуть отрицательную обратную связь. Для тех же значений по ЛЧХ измерить значение частоты единичного усиления разомкнутой САУ и величину запаса по фазе.

6. Для замкнутой САУ со структурой, соответствующей пункту 3, определить динамическую ошибку при единичном ступенчатом и линейном воздействиях.

Указание: сформировать линейно изменяющееся входное воздействие дополнительным звеном с передаточной функцией . Для наблюдения сигнала ошибки ввести в структурную схему на входе звено с передаточной функцией .

Содержание отчета

Графики переходных процессов.

Передаточные функции и логарифмические частотные характеристики разомкнутых систем. Передаточные функции замкнутых систем.

Значения характерных частот, запасов по фазе и соответствующие им длительности переходных процессов. Динамические ошибки при типовых воздействиях.

Выводы о взаимосвязи частотных характеристик и качества переходного процесса.