Приложение ж (обязательное)
D – разбиение плоскости одного параметра
Пример. Построить границу D – разбиения по коэффициенту усиления K для системы автоматического регулирования, передаточная функция которой в разомкнутом состоянии имеет вид:
Решение:
Передаточная функция в замкнутом состоянии:
Характеристическое уравнение
D(s)
=
Уравнение
границы D – разбиения получим, подставляя
в характеристическое уравнение
из которого находим K
Выделим вещественную и мнимую часть:
вещественная
часть
мнимая
часть
Задаваясь различными значениями , находим и .
Таблица Е1 – Расчет границы D-разбиения
-
-5
-4
-2
-1
0
1
2
4
5
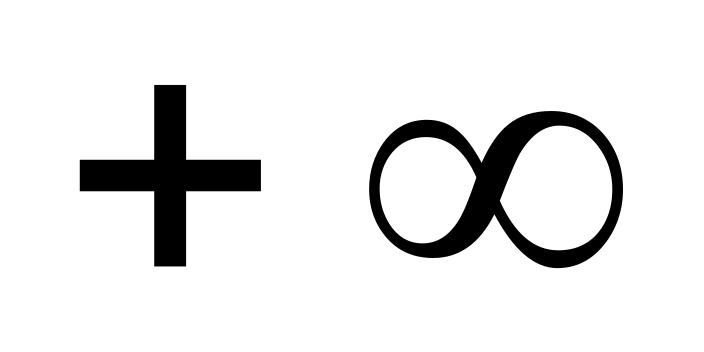
5,25
3
0
-0,75
-1
-0,75
0
3
5,25
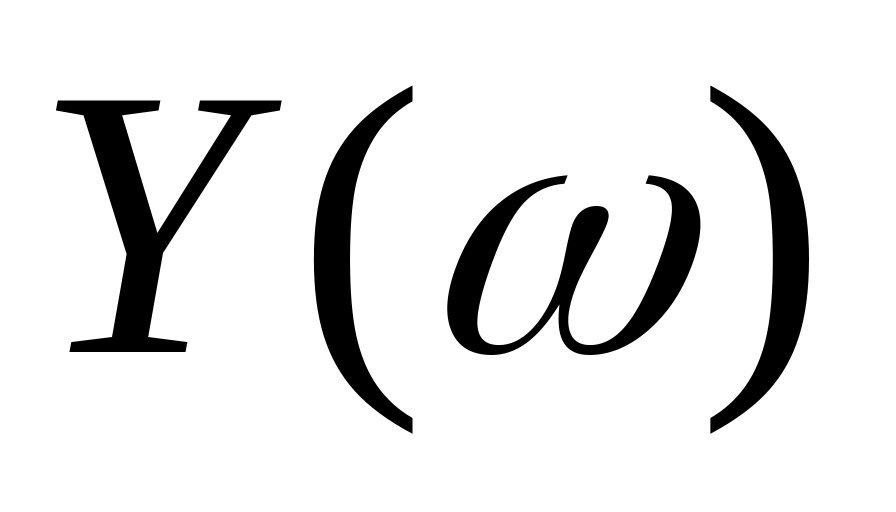
-2
2
3,4
2
0
-2
-3,4
-2
2
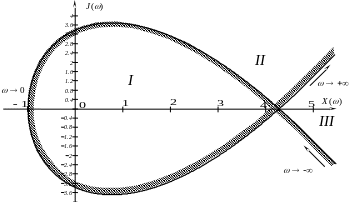
По полученным значениям строим кривую D – разбиения.
-4
Рисунок Е1 – Кривая D-разбиения плоскости одного параметра
Заштрихуем её, пользуясь правилом штриховки: двигаясь по кривой D-разбиения при изменении частоты от - до + , наносим штриховку слева.
Комплексная
плоскость
разбивается кривой D-разбиения на 3
области: I,
II,
III.
Областью – претендентом является область I, так как штриховка направлена внутрь ее.
Проверяем, является ли область I областью устойчивости.
Возьмём любое К в этой области, например, К=1. Подставим его в характеристическое уравнение:
.
Определяем устойчивость системы, пользуясь критерием Гурвица.
Главный определитель Гурвица:
.
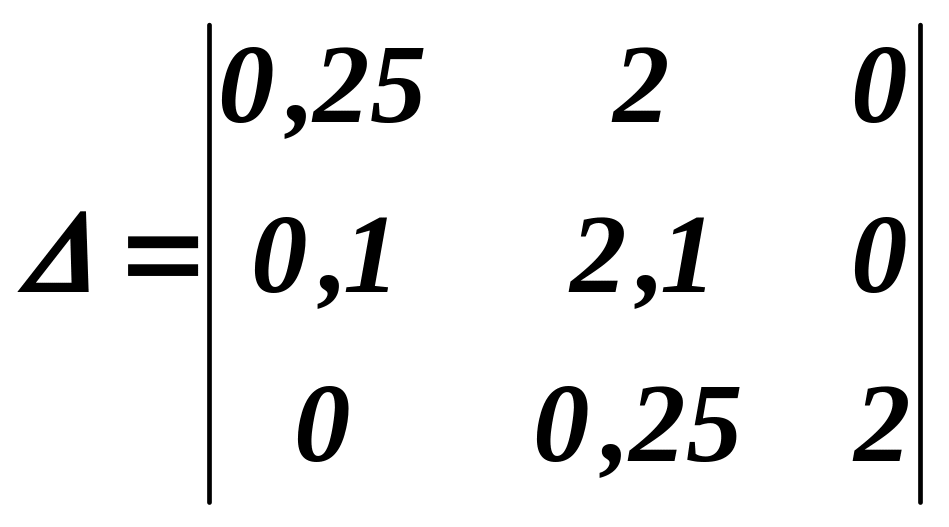Диагональные миноры:
;
.
Все диагональные миноры положительны, система устойчива.
При
К=1
система устойчива, следовательно,
область I
будет областью устойчивости (число
правых корней равно 0), т.е. при любом
,
система будет устойчивой. Область
реальных значений, при которых система
будет устойчива, ограничивается
положительными вещественными значениями
0<К<4,25.
Пользуясь правилами перехода, определим число правых корней m в области II и III. В области II m =1, так как при переходе из области I в область II граница D-разбиения пересекается против штриховки. В области III m =2. Таким образом, имеем области D(0), D(1), D(2). Область D(3) в данном случае отсутствует. Это означает, что при заданных параметрах системы и любом значении К, невозможно, чтобы все три корня характеристического уравнения одновременно были правыми.