2.4. Амплитудная манипуляция последовательностью прямоугольных импульсов

Пусть модулирующий сигнал представляет последовательность прямоугольных импульсов (рис. 4, а). В общем случае при амплитудной манипуляции с учетом выражений (2) и (3) модулируемый сигнал (рис. 4, б) будет иметь два значения: максимальное и минимальное .

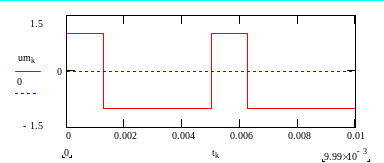
а

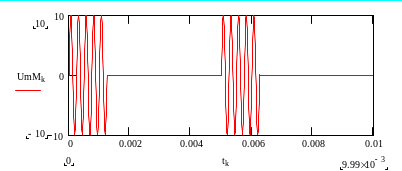
б

Рис. 4. Амплитудная манипуляция: а – модулирующий сигнал; б – амплитудно-манипулированное колебание

Часто при амплитудной манипуляции выбирают . Тогда , , т.е. для сообщений закодированных, например, двоичных кодов, при передаче символа 1 несущая излучаться будет, при передаче символа 0 излучение отсутствует. Если импульсы последовательности имеют большую скважность, например при фазово-импульсной модуляции, то при импульсная мощность несущей соответственно возрастает, что позволяет в каналах связи увеличить дельность передачи или снизить действие помех. Последовательность прямоугольных импульсов можно рассматривать как сложный сигнал, состоящий из отдельных гармонических составляющих. Эти составляющие можно получить из разложения исходного сигнала в ряд Фурье [2]:

,

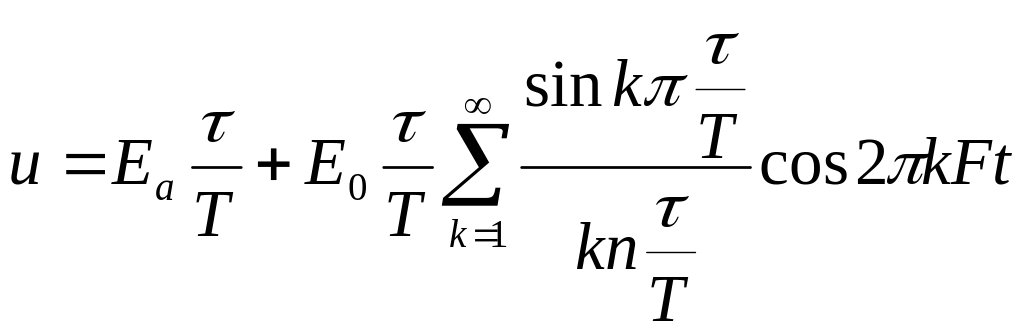где - частота следования импульсов.

Как уже отмечалось, каждая составляющая с частотой , входящая в спектр прямоугольных импульсов, обусловит появление в спектре манипулированного сигнала двух боковых частот и . Спектр прямоугольных импульсов приведен на рис. 5, а, а спектр манипулированного сигнала – на рис. 5, б.

В общем случае, когда известен спектр модулированного сигнала, спектр АМ-колебания можно построить по следующему правилу: сместить спектр модулирующего сигнала на интервал частот, равный несущей частоте

, и зеркально отобразить относительно спектральной линии на несущей частоте.

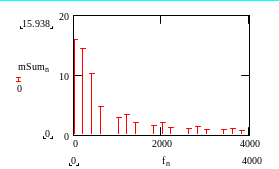
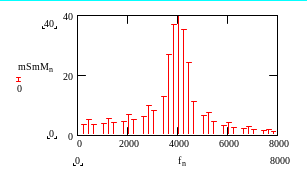
а б

Рис. 5. а – последовательности прямоугольных импульсов;

б – амплитудно-манипулированного сигнала

3. Порядок выполнения работы

3.1. Амплитудная модуляция гармонического переносчика простым сигналом.

3.1.1. Задайте параметры гармонического переносчика и модулирующего сигнала.

f₀=2000 Гц – частота несущего сигнала;

U₀ = 1 В – амплитуда немодулированного сигнала;

m=0.8 – коэффициент (глубина) модуляции);

F_m =200 Гц – частота модулирующего сигнала;

U_c =1 В – амплитуда модулирующего сигнала.

3.1.2. Задайте оба сигнала как функции времени:

- длительность наблюдаемого процесса в секундах;

К = 1024 – число точек, описывающих процесс;

- интервалы времени между точками;

k = 0…K-1 – номера точек;

t_k = k × dt – текущее время;

гармонический переносчик:

UP_k = U₀ × sin(2 p f₀ t_k);

модулирующий гармонический сигнал:

UM_k = U_c × sin(2 p F₀ t_k);

тональная амплитудная модуляция гармонического переносчика:

Uam_k = UP_k + UP_k *UM_k m.

3.1.3. Постройте графики исходных сигналов и модулированного сигнала и зафиксируйте их (на любом носителе) для представления в отчете. Все последующие графики также должны быть представлены в отчете.

3.1.4. Рассчитайте спектры сигналов

- номера гармонических составляющих спектра;

- текущая частота.

Спектр гармонического модулирующего сигнала:

SM = 2*CFFT(UM) – комплексный спектр;

MSM_n = çSM_nç - спектр амплитуд.

Спектр гармонического переносчика:

SP =2*CFFT(UP) – комплексный спектр;

MSP_n = çSP_nç- спектр амплитуд.

Спектр сигнала с амплитудной модуляцией:

Sam = 2*CFFT(Uam) – комплексный спектр;

mSam_n = çSam_nç- спектр амплитуд.

3.1.5. Постройте спектр амплитуд всех сигналов.