Теорема 2.7.

Если несократимая дробь 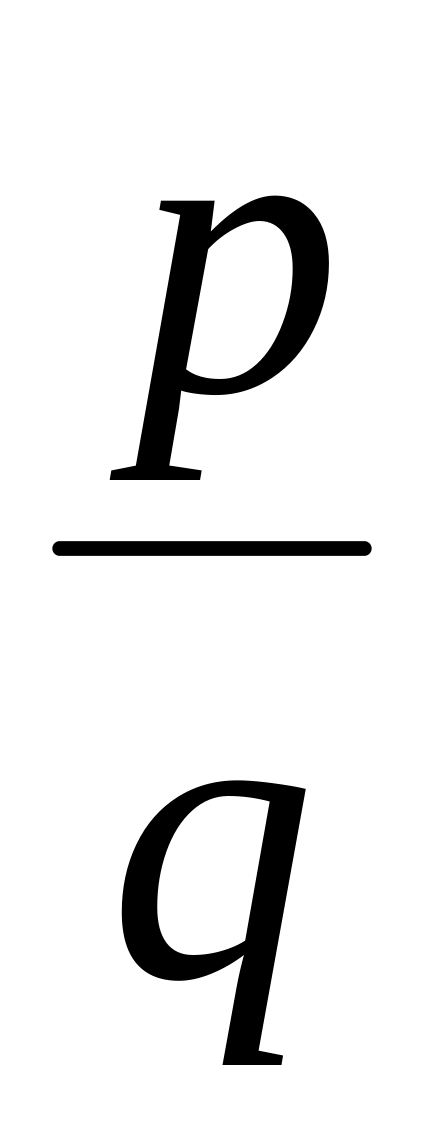является корнем многочлена Р(z) = а_пz^п + а_п–1z^п–1 + ... + а₁z + а₀ с целыми коэффициентами, то число р является делителем свободного члена а₀, а число q – делителем старшего коэффициента а_п.

Доказательство:

Пусть корень многочлена Р(z) = а_пz^п + а_п–1z^п–1 + ... + а₁z + а₀, значит, . Умножим обе части этого равенства на qⁿ, получим

а_пp^п + а_п–1p^п–1q + ... + а₁pq^n-1 + а₀qⁿ = 0.

Перепишем полученное равенство двумя способами:

а_пp^п = q(–а_п–1p^п–1– ... – а₁pq^n-2 – а₀q^n–1)

и а₀qⁿ = р(– а_пp^п–1 – а_п–1p^п–2q – ... – а₁q^n-1)

Так как р не делится на q и наоборот, то из первого равенства следует, что число q есть делитель числа а_п, а из второго равенства – что р есть делитель коэффициента а₀. Теорема доказана.

Следствие 1.

Если многочлен с целыми коэффициентами имеет целый корень, то этот корень есть делитель свободного члена.

Таким образом, если многочлен с целыми коэффициентами имеет целые корни, то их нужно искать среди делителей свободного члена.

Следствие 2.

Если старший коэффициент многочлена с целыми коэффициентами равен единице, то все рациональные корни этого многочлена (если они существуют) есть целые числа.

Теорема 2.8.

Для того, чтобы число α являлось корнем кратности k многочлена

Р(z) = а_пz^п + а_п–1z^п–1 + ... + а₁z + а₀, необходимо и достаточно выполнение условий:

, а .

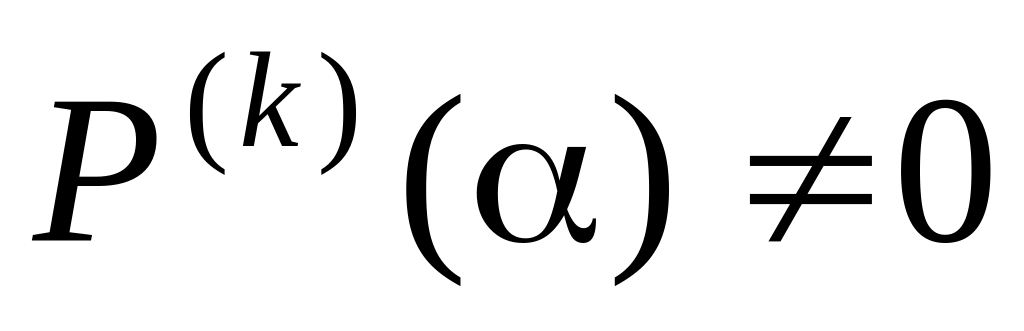7