2. Практическая часть.
2.1 Решение нелинейных уравнений в Excel.
Рассматриваемое уравнение x3+25x+19=0.
Левую часть уравнения обозначим за f(x):
f(x) = x3+25x+19.
Протабулируем функцию f(x) на интервале [-1;-0,5] с шагом h = 0,05.
x |
f(x) |
-1 |
-6 |
-0,95 |
-4,75 |
-0,9 |
-3,5 |
-0,85 |
-2,25 |
-0,8 |
-1 |
-0,75 |
0,25 |
-0,7 |
1,5 |
-0,65 |
2,75 |
-0,6 |
4 |
-0,55 |
5,25 |
-0,5 |
6,5 |
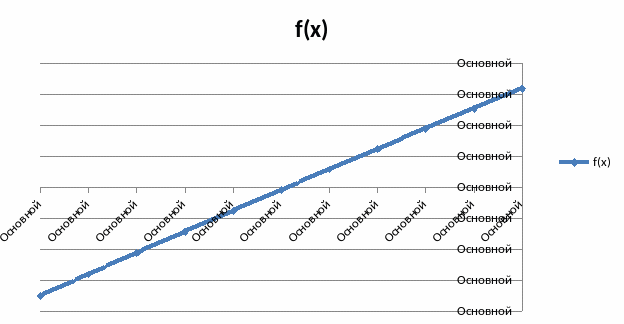
Проанализируем данные таблицы на интервале [-0,75; -0,7].
Нахождение корня уравнения
x |
f(x) |
-0,74357 |
-0,00037 |
Нахождение корня методом половинного деления.
a |
x |
b |
f(a) |
f(x) |
f(a)*f(x) |
|f(x)|<e |
-0,744 |
-0,7415 |
-0,739 |
-0,01183 |
0,054807 |
-0,00065 |
считаем |
-0,744 |
-0,74275 |
-0,7415 |
-0,01183 |
0,021491 |
-0,00025 |
считаем |
-0,744 |
-0,74338 |
-0,74275 |
-0,01183 |
0,004831 |
-5,7E-05 |
считаем |
-0,744 |
-0,74369 |
-0,74338 |
-0,01183 |
-0,0035 |
4,14E-05 |
считаем |
-0,74369 |
-0,74353 |
-0,74338 |
-0,0035 |
0,000666 |
-2,3E-06 |
считаем |
-0,74369 |
-0,74361 |
-0,74353 |
-0,0035 |
-0,00142 |
4,96E-06 |
считаем |
-0,74361 |
-0,74357 |
-0,74353 |
-0,00142 |
-0,00038 |
5,32E-07 |
корень |
Нахождение корня методом Ньютона.
e= |
0,000001 |
|
|
x |
f(x) |
f'(x) |
|f(x)|<e |
-0,6 |
3,784 |
26,08 |
считаем |
-0,74509 |
-0,04095 |
26,66549 |
считаем |
-0,74356 |
-5,3E-06 |
26,65863 |
считаем |
-0,74356 |
-8,9E-14 |
26,65863 |
корень |
2.2 Решение систем нелинейных уравнений в Excel.
Дана система уравнений:
,
где
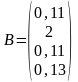
D= |
1,2114 |
Метод обратной матрицы.
-3,0571 |
1,3101 |
-0,9645 |
1,9898 |
|
X1= |
2,4364 |
1,6949 |
-0,2641 |
0,1961 |
-0,2308 |
|
X2= |
-0,3501 |
0,9193 |
0,1750 |
0,6384 |
-0,6986 |
=А-1 |
X3= |
0,4305 |
1,9714 |
0,0325 |
0,6276 |
-1,3855 |
|
X4= |
0,1708 |
Метод Крамера.
0,11 |
0,75 |
-0,18 |
0,21 |
|
D1= |
2,9515 |
2 |
0,13 |
0,11 |
1 |
|
|
|
0,11 |
0,11 |
3,01 |
-2,01 |
|
|
|
0,13 |
1,12 |
1,11 |
-1,31 |
|
|
|
|
|
|
|
|
|
|
0,17 |
0,11 |
-0,18 |
0,21 |
|
D2= |
-0,4241 |
0,75 |
2 |
0,11 |
1 |
|
|
|
-0,33 |
0,11 |
3,01 |
-2,01 |
|
|
|
0,11 |
0,13 |
1,11 |
-1,31 |
|
|
|
|
|
|
|
|
|
|
0,17 |
0,75 |
0,11 |
0,21 |
|
D3= |
0,5216 |
0,75 |
0,13 |
2 |
1 |
|
|
|
-0,33 |
0,11 |
0,11 |
-2,01 |
|
|
|
0,11 |
1,12 |
0,13 |
-1,31 |
|
|
|
|
|
|
|
|
|
|
0,17 |
0,75 |
-0,18 |
0,11 |
|
D4= |
0,2070 |
0,75 |
0,13 |
0,11 |
2 |
|
|
|
-0,33 |
0,11 |
3,01 |
0,11 |
|
|
|
0,11 |
1,12 |
1,11 |
0,13 |
|
|
|
|
|
|
|
|
|
|
X1= |
2,4364 |
|
|
|
|
|
X2= |
-0,3501 |
|
|
|
|
|
X3= |
0,4305 |
|
|
|
|
|
X4= |
0,1708 |
|
|
|
|
|