Чтобы выяснить состояние этой системы, достаточно задать один вопрос, например: находится ли система в состоянии х{! Ответ «да» или «нет» на этот вопрос доставляет некоторую информацию, которая достигает своего максимального значения 1, когда оба состояния априори равновероятны: p₁=p₂=1/2. Таким образом, максимальная информация, даваемая ответом «да» или «нет», равна одной двоичной единице.

Если информация от какого-то сообщения равна n двоичным единицам, то она равносильна информации, даваемой n ответами «да» или «нет» на вопросы, поставленные так, что «да» и «нет» одинаково вероятны.

В некоторых простейших случаях для выяснения содержания сообщения действительно удается поставить несколько вопросов так, чтобы ответы «да» и «нет» на эти вопросы были равновероятны. В таких случаях полученная информация фактически измеряется числом таких вопросов.

Если же поставить вопросы точно таким образом не удается, можно утверждать только, что минимальное число вопросов, необходимое для выяснения содержания данного сообщения, не меньше, чем информация, заключенная в сообщении. Чтобы число вопросов было минимальным, нужно формулировать их так, чтобы вероятности ответов «да» и «нет» были как можно ближе к 1/2.

3-12. Некто задумал любое целое число X от единицы до восьми

1. <Х<2 ^ _{а нам} предлагается угадать его, поставив минимальное число вопросов, на каждый из которых дается ответ «да» или «нет».

Решение: Определяем информацию, заключенную в сообщении, какое число задумано. Априори все значения X от 1 до 8 одинаково вероятны:

Ответ: Минимальное число вопросов, которые нужно поставить для выяснения задуманного числа, не меньше трех.

В данном случае можно, действительно, обойтись тремя вопросами, если сформулировать их так, чтобы вероятности ответов «да» и «нет» были равны.

Пусть, например, задумано число «пять», мы этого не знаем и задаем вопросы:

Вопрос 1. Число X меньше пяти?

Ответ. Нет. (Вывод: X - одно из чисел 5, 6, 7, 8.)

Вопрос 2. Число X меньше семи?

Ответ. Да. (Вывод: X - одно из чисел 5, 6.)

Вопрос 3. Число X меньше шести?

Ответ. Да. (Вывод: число X равно пяти.)

12

Легко убедиться, что тремя такими (или аналогичными) вопросами можно установить любое задуманное число от 1 до 8.

Задания для самостоятельного выполнения.

Вариант 1.

1. Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8x8, после первого хода первого игрока, играющего крестиками?

2. Определите время (сек.) необходимое для передачи модемом (со скоростью передачи 28800 бит/с) цветного растрового изображения размером 640х480 пикселей при условии, что цвет каждого пикселя кодируется тремя байтами.

Вариант 2.

1. В рулетке общее количество лунок равно 128. Какое количество информации мы получаем в зрительном сообщения об остановке шарика в одной из лунок?

2. Рассчитать необходимый объем видеопамяти для графического режима с разрешением 800х600 точек и глубиной цвета 24 бита на точку.

Вариант 3.

1. Происходит выбор одной карты из колоды в 32 карты. Какое количество информации мы получаем в зрительном сообщении о выборе определенной карты?

2. Сообщение из 50 символов было записано в 8-битной кодировке Windows-1251. После вставки в текстовый редактор сообщение было перекодировано в 16-битный код Unicode. Определите на сколько байт увеличился объем памяти, занимаемый сообщением.

Вариант 4.

1. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся:

а) 25 белых, 25 красных, 25 синих и 25 зеленых шариков;

б) 30 белых, 30 красных, 30 синих и 10 зеленых шариков.

2. Автоматическое устройство осуществило перекодировку информационного сообщения, первоначально записанного в коде Windows-1251, в кодировку Unicode. При этом информационное сообщение увеличилось на 400 бит. Определите длину сообщения в символах.

Вариант 5.

1. Какое количество вопросов достаточно задать вашему собеседнику, чтобы точно определить день и месяц его рождения?

2. Оцените информационный объем следующего предложения в кодировке Unicode и ASCII «Один пуд - около 16,4 килограмм».

13

Вариант 6.

1. Заполнить пропуски числами:

а) 5 Кбайт = байт = бит,

б ) Кбайт = байт = 12288 бит;

в ) Кбайт = байт = 2¹³ бит;

г ) Гбайт =1536 Мбайт = Кбайт;

д) 512 Кбайт = 2 байт = 2 бит.

2. Сканируется цветное изображение 10х10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Определите информационный объем полученного графического файла.

Вариант 7.

1. Найти x из следующих соотношений:

а) 16^x бит = 32 Мбайт;

б) 8^х Кбайт = 16 Гбайт.

2. Для хранения неупакованного растрового изображения размером 32х32 пикселя потребовалось 512 байт памяти. Определите максимально возможное число цветов в палитре изображения.

Вариант 8.

1. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/512 часть одного мегабайта.

2. Закодируйте с помощью кодировочной таблицы ASCII и представьте в шестнадцатеричной системе счисления слово «Data».

Вариант 9.

1. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере равна 256. Какое количество информации в байтах может ввести пользователь в компьютер за 1 минуту.

2. Вычислить объем видеофайла в Гб длительностью 64 сек, скоростью смены кадров равной 32 кадров/сек, разрешении 1280х640 точек и разрядностью цвета 16 бит. Объемом звуковой составляющей видеоклипа можно пренебречь.

Вариант 10.

1. Система оптического распознавания символов позволяет преобразовывать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65536 символов. Какое количество информации будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов.

2. Используется кодовая таблица СР-1251 (Windows Cyrillic). Файл в простом текстовом формате, если в тексте 200 страниц, на странице 32 строки, а в строке в среднем 48 символов, Определите размер файла в килобайтах.

14

Основание	Н азвание	Алфавит
п= 2	Двоичная	01
п = 3	Троичная	012
п- 8	Восьмеричная	01234567
П= 16		01234567S9A8CDEF

Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например:

15

1011012, 36718, 3B8F16.

В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1, ..., q-1. Запись числа q в q-ичной системе счисления имеет вид 10.

Развернутая форма записи числа. Пусть A_q - число в системе с основанием q, а1 - цифры данной системы счисления, присутствующие в записи числа A, n+1 - число разрядов целой части числа, m - число разрядов дробной части числа:

Развернутой формой числам называется запись в виде:

Например, для десятичного числа:

В следующих примерах приводится развернутая форма шестнадцатеричного и двоичного чисел: ^

В любой системе счисления ее основание записывается как 10.

Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную. Например, перевод в десятичную систему написанных выше чисел производится так:

Перевод десятичных чисел в другие системы счисления

Перевод целых чисел. Целое десятичное число X требуется перевести в систему с основанием q: X = (a_na_n-1 ^a₁a₀)_q. Нужно найти значащие цифры числа: a₀, a₁, ..., a_n. Представим число в развернутой форме и выполним тождественное преобразование:

Отсюда видно, что a0 есть остаток от деления числа X на число q. Выражение в скобках - целое частное от этого деления. Обозначим его за X1. Выполняя аналогичные преобразования, получим:

16

Следовательно, a₁ есть остаток от деления X1 на q. Продолжая деление с остатком, будем получать последовательность цифр искомого числа. Цифра a_n в этой цепочке делений будет последним частным, меньшим q.

Сформулируем полученное правило: для того чтобы перевести целое десятичное число в систему счисления с другим основанием, нужно:

1. основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить по правилам десятичной арифметики;

2. последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;

3. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

4. составить число в новой системе счисления, записывая его, начиная с последнего частного.

Пример 1. Перевести число 37ю в двоичную систему.

Для обозначения цифр в записи числа используем символику: О5О4О3О2О1О0

Отсюда: 37₁₀ = l00l0l₂

Пример 2. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы:

Отсюда следует: 315₁₀ = 473₈ = 13B₁₆. Напомним, что 11₁₀ = B

-46-

Перевод десятичных дробей. Десятичную дробь X<1 требуется перевести в систему с основанием q: X=(0, a_-1a_-2 ... a__m+i a_-m)_q.

Нужно найти значащие цифры числа: a_-1, a_-2, ., a_-m. Представим число в развернутой форме и умножим его на q\

Отсюда видно, что a_-1 есть целая часть произведения X на число q. Обозначим за XI дробную часть произведения и умножим ее на q:

17

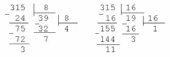
Следовательно, a-2 есть целая часть произведения X1 на число q. Продолжая умножения, будем получать последовательность цифр. Теперь сформулируем правило: для того чтобы перевести десятичную дробь в систему счисления с другим основанием, нужно: последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления; полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления; составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения. Пример 3. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы. 0		1875 * 3
1		5000 *3
4		0000
0	1-375 * 2
0	3750 к 2
0	7500 * 2
1	5000 * 2
1	0000
0			1&75 х 15
3			0000

Здесь в левом столбце находится целая часть чисел, а в правом — дробная.

Отсюда: 0,1875ю = 0,00112 = 0,14s = 0,3i6

Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).

Перевод чисел между системами счисления 2 - 8 - 16

Представление информации, хранящейся в компьютерной памяти в ее истинном двоичном виде, весьма громоздко из-за большого количества цифр. Имеется в виду запись такой информации на бумаге или вывод ее на экран. Для этих целей принято использовать смешанные двоично-восьмеричную или двоично-шестнадцатеричную системы.

Существует простая связь между двоичным и шестнадцатеричным представлением числа. При переводе числа из одной системы в другую одной шестнадцатеричной цифре соответствует четырехразрядный двоичный код. Это соответствие отражено в двоично-шестнадцатеричной таблице:

Двоично-шестнадцатеричная таблица

18

16	2	16	2
0	0000	8	1000
1	0001	9	1001
2	0010	А	1010
3	0011	В	1011
4	0100	с	1100
5	01 01	D	1101
6	0110	Е	1110
7	0111	F	1111

Такая связь основана на том, что 16 = 2⁴ и число различных четырехразрядных комбинаций из цифр 0 и 1 равно 16: от 0000 до 1111. Поэтому перевод чисел из шестнадцатеричных в двоичные и обратно производится путем формальной перекодировки по двоично­шестнадцатеричной таблице.

Вот пример перевода 32-разрядного двоичного кода в 16-ричную систему:

1011 1100 0001 0110 1011 1111 0010 1010 -» BC16BF2A

Если дано шестнадцатеричное представление внутренней информации, то его легко перевести в двоичный код. Преимущество шестнадцатеричного представления состоит в том, что оно в 4раза короче двоичного.

В двоично-восьмеричной системе каждой восьмеричной цифре соответствует триада двоичных цифр. Эта система позволяет сократить двоичный код в 3 раза.

Представление и обработка в компьютере вещественных чисел. Формат представления вещественных чисел в компьютере называется форматом с плавающей точкой. Вещественное число R представляется в виде произведения мантиссы m на основание системы счисления n в некоторой целой степенир, которую называют порядком: R=m*n^p.

Представление числа в форме с плавающей точкой неоднозначно. Например, для десятичного числа 25,324 справедливы следующие равенства:

25,324 = 2,5324 • 10¹ = 0,0025324 • 10⁴ = 2532,4 • 10^-2 и т.п.

Чтобы не было неоднозначности, договорились в ЭВМ использовать нормализованное представление числа в форме с плавающей точкой.

Мантисса в нормализованном представлении должна удовлетворять условию: 0,1_н - т < \_п. Иначе говоря, мантисса меньше единицы и первая значащая цифра - не ноль. В некоторых случаях условие нормализации принимают следующим: 1_н - т < 10„.

В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.

В разных типах компьютеров применяются различные варианты представления чисел в форме с плавающей точкой. Рассмотрим один из вариантов внутреннего представления вещественного числа в четырехбайтовой ячейке памяти.

В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы.

19

В старшем бите 1-го байта хранится знак числа: 0 обозначает плюс, 1 - минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).

В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. Значит, машинный порядок изменяется в диапазоне от 0 до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным, так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от -64 до 63.

Машинный порядок смещен относительно математического и имеет только положительные значения. Смещение выбирается так, чтобы минимальному математическому значению порядка соответствовал ноль.

Связь между машинным порядком (Mp) и математическим (p) в рассматриваемом случае выражается формулой: Mp = p + 64.

Полученная формула записана в десятичной системе. В двоичной системе формула имеет вид: Mp₂ = p₂ + 100 0 0 00₂.

Для записи внутреннего представления вещественного числа необходимо:

1. перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами,

2. нормализовать двоичное число,

3. найти машинный порядок в двоичной системе счисления,

4. учитывая знак числа, выписать его представление в четырехбайтовом машинном слове.

Пример. Записать внутреннее представление числа 250,1875 в форме с плавающей

точкой.

Решение

1. Переведем его в двоичную систему счисления с 24 значащими цифрами: 250,1875₁₀ = 11111010,00110000000000002.

2. Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,111110100011000000000000 • 10₂¹⁰⁰⁰.

Здесь мантисса, основание системы счисления (2₁₀ = 10₂) и порядок (8₁₀ = 1000₂) записаны в двоичной системе.

3. Вычислим машинный порядок в двоичной системе счисления:

Mp2 = 1000 + 100 0000 = 100 1000.

4. Запишем представление числа в четырехбайтовой ячейке памяти с учетом знака числа

20

О 1001000 11111010 00110000 00000000

31 24 23 0

Шестнадцатеричная форма: 48FA3000.

Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю.

Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в форме с плавающей точкой — это число с самой большой мантиссой и самым большим порядком.

Для четырехбайтового машинного слова таким числом будет:

1. 111111111111111111111111 • 10₂^1111111.

После перевода в десятичную систему счисления получим:

МАХ = (1 - 2^-24) • 2⁶³ * 10¹⁹.

Если при вычислениях с вещественными числами результат выходит за пределы допустимого диапазона, то выполнение программы прерывается. Такое происходит, например, при делении на ноль, или на очень маленькое число, близкое к нулю.

Вещественные числа, разрядность мантиссы которых превышает число разрядов, выделенных под мантиссу в ячейке памяти, представляются в компьютере приближенно (с “обрезанной” мантиссой). Например, рациональное десятичное число 0,1 в компьютере будет представлено приближенно (округленно), поскольку в двоичной системе счисления его мантисса имеет бесконечное число цифр. Следствием такой приближенности является погрешность машинных вычислений с вещественными числами.

Вычисления с вещественными числами компьютер выполняет приближенно. Погрешность таких вычислений называют погрешностью машинных округлений.

Множество вещественных чисел, точно представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Дискретность является следствием ограниченного числа разрядов мантиссы, о чем говорилось выше.

Количество вещественных чисел, точно представимых в памяти компьютера, можно вычислить по формуле: N =2^t ■ (U- L +1) + 1. Здесь t - количество двоичных разрядов мантиссы; U - максимальное значение математического порядка; L - минимальное значение порядка. Для рассмотренного выше варианта представления (t =24, U =63, L =-64) получается: N = 2 146 683 548.

Двоичная нумерация. В таблице кодировки внутренний двоичный код символа - это его порядковый номер в двоичной системе счисления. Например, номер буквы S в таблице ASCII равен 83. Восьмиразрядный двоичный код буквы S равен значению этого числа в двоичной системе счисления: 01010011.

21

Двоичные вычисления. Согласно принципу Джона фон Неймана, компьютер производит вычисления в двоичной системе счисления. В рамках базового курса достаточно ограничиться рассмотрением вычислений с целыми двоичными числами. Для выполнения вычислений с многозначными числами необходимо знать правила сложения и правила умножения однозначных чисел. Вот эти правила:

Принцип перестановочности сложения и умножения работает во всех системах счисления. Приемы выполнения вычислений с многозначными числами в двоичной системе аналогичны десятичной. Иначе говоря, процедуры сложения, вычитания и умножения “столбиком” и деления “уголком” в двоичной системе производятся так же, как и в десятичной.

Рассмотрим правила вычитания и деления двоичных чисел. Операция вычитания является обратной по отношению к сложению. Из приведенной выше таблицы сложения следуют правила вычитания:

1. - 0 = 0; 1 - 0 = 1; 10 - 1 = 1.

Вот пример вычитания многозначных чисел:

1001101101

100110110

Полученный результат можно проверить сложением разности с вычитаемым. Должно получиться уменьшаемое число.

Деление - операция обратная умножению. В любой системе счисления делить на 0 нельзя. Результат деления на 1 равен делимому. Деление двоичного числа на 10₂ ведет к перемещению запятой на один разряд влево, подобно десятичному делению на десять. Например:

Деление на 100 смещает запятую на 2 разряда влево и т.д.

Задания для самостоятельного выполнения

Вариант1.

1. Переведите десятичные числа в СС с основаниями 2, 8, 16 и обратно.

1. 545,46₁₀

2. 713,25ю

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 11100,1001₂+1110,011₂

2. 9F3,4516-FF,D216

Вариант 2.

1. Переведите двоичные числа в СС с основаниями 8, 10, 16 и обратно.

1. 101010,101012

2. 111001,001012

22

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 416,328 + 255,718

2. 1D0,8216-C8,B216 Вариант 3.

1. Переведите шестнадцатеричные числа в СС с основаниями 2, 10, 8 и обратно.

1. 3E5,65₁₆

2. 814,AF16

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 723,42₈ + 136,17₈

2. 11011,112 - 1011,012 Вариант 4.

1. Переведите восьмеричные числа в СС с основаниями 2, 10, 16 и обратно.

1. 312,478

2. 674,358

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 506,F416 + ABC,6216

2. 11011,112 - 1011,012 Вариант 5.

1. Переведите шестнадцатеричные числа в СС с основаниями 2, 10, 8 и обратно.

1. A16,F116

2. 23С,9Е16

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 267,458 + 345,28

2. 1111,112 - 1100,1112 Вариант 6.

1. Переведите восьмеричные числа в СС с основаниями 2, 10, 16 и обратно.

1. 343,578

2. 713,628

2. Представьте результат вычисления арифметических операций в указанной СС.

1. 101011,1012+1111,01012

2. C5D,5816-B8E,4616 Вариант 7.

1. Переведите десятичные числа в СС с основаниями 2, 8, 16 и обратно.

1. 387,1210

2. 854,3610

23