Рекомендации по выполнению работы.

Цель работы: Ознакомление с методом статистических испытаний на примере определения гарантированной скорости сквозного пробития бронированной преграды, путем моделирования бронепробития.

Задачи работы:

1. изучить сущность метода статистических испытаний;

2. изучить методы проверки согласия статистического и теоретического законов распределения;

3. изучить стохастическую модель бронепробития;

4. произвести обработку и анализ результатов расчета.

Теоретический материал

Метод Монте-Карло: Метод статистических испытаний заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Таким образом , метод Монте-Карло - это численный метод решения математической задачи при помощи моделирования случайных величин . Метод основан на многократном проведении испытаний построенной модели с последующей статистической обработкой для определения характеристик рассматриваемого процесса в виде статистических оценок его параметров .

Этот метод целесообразно применять при исследовании систем, функционирование которых определяется многими вероятностными параметрами элементарных явлений; когда построение чисто аналитической вероятностной модели такой системы затруднено. Он базируется на использовании случайных чисел - возможных значений некоторой случайной величины с заданным законом распределения.

Стохастическая модель: Все наблюдаемые процессы, характеризующие физические явления, можно классифицировать в общем виде как детерминированные и недетерминированные. К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями. Математические модели движения снаряда в канале ствола орудия, в воздухе после вылета из канала ствола, являются детерминированными. Однако в действительности ни один реальный физический процесс нельзя считать строго детерминированным, поскольку всегда существует возможность того, что какое-то непредвиденное событие изменит течение процесса таким образом, что полученные результаты будут носить иной характер, чем предполагалось ранее.

Полной статистической характеристикой случайной величины является закон распределения. Очень важное практическое значение имеет нормальное распределение, которое наиболее часто используется на практике. В данной лабораторной работе будем исходить из того, что полученная нами характеристика распределяется по нормальному закону и, в дальнейшем, постараемся доказать, что это именно так.

Применительно к гипотезе первого типа, т.е. к гипотезе Н₀: M[ (x)] F(x), используются критерий Пирсона, для оценки степени согласованности эмпирического и теоретического распределений

Рассмотрим статистику критерия Пирсона или ²-критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина Х приняла определенные значения. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда:

Ji	x1, x2	x2, x3	...	xi, xi+1	...	xk, xk+1
			...		...

, ,

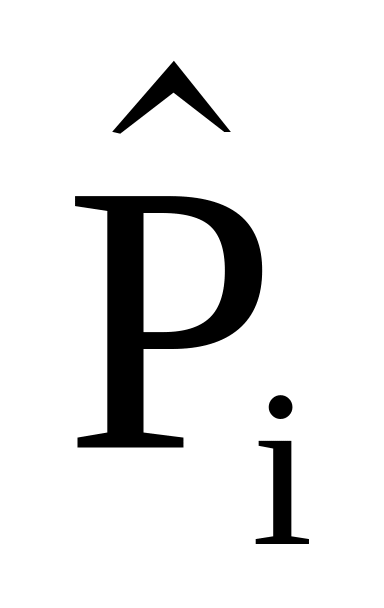
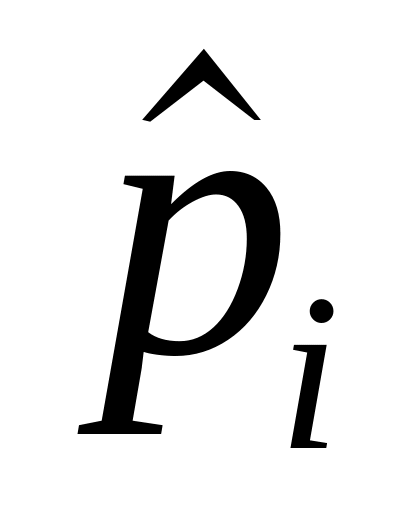
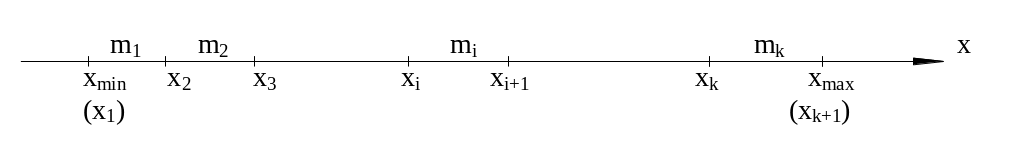
где J_i - i-й интервал (разряд),

k - общее число интервалов,

m_i - число значений в i-м разряде (число измерений величины Х, попавших в i-й разряд).

Величина R= x_max - x_min называется размахом выборки.

Зная F(x), можно найти теоретические вероятности попадания величины Х в каждый из разрядов:

, ... , , ... , .

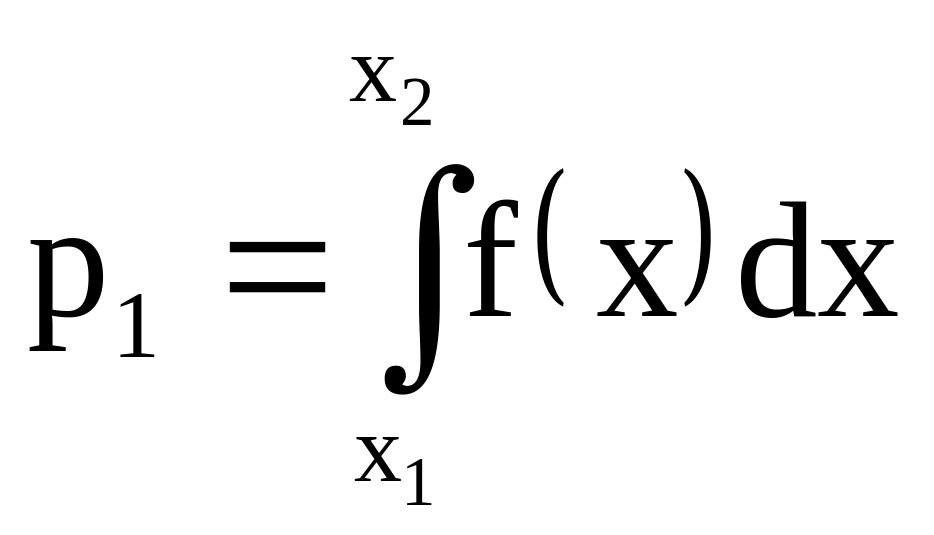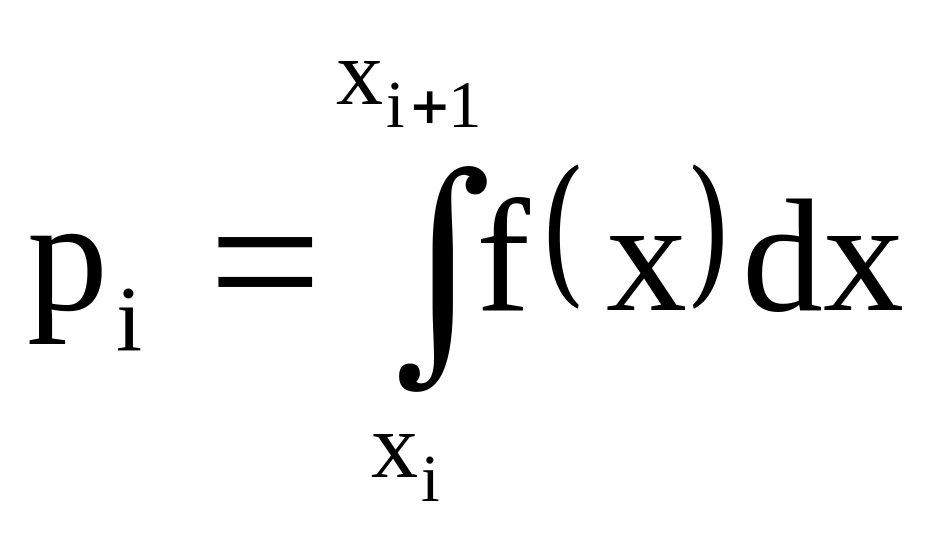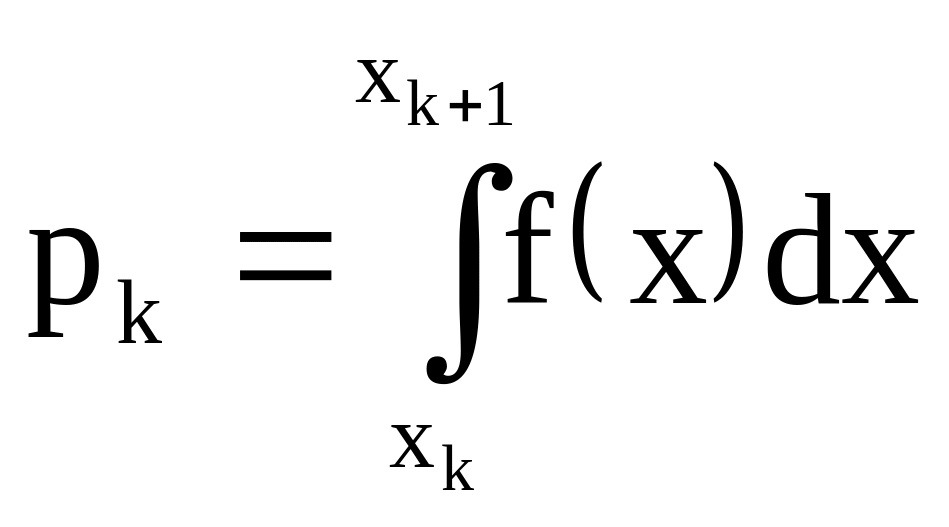Пусть .

Если , то .

Это и есть статистика Пирсона.

Величина V имеет ²- распределение.

Критическое значение ₂=²_кр табулировано и находится по уровню значимости  и числу степеней свободы =k-l-1, где l - количество связей, определяемое числом оценок параметров, вычисленных по данным выборки. Так для нормального распределения l=2, если оба параметра m_x и _x² рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот , т.е. числу разрядов. Число независимых условий («связей»), накладываемых на частоты , равно 1, если мы требуем, чтобы (это требование накладывается всегда). Число «связей» возрастает до 2, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистические средние, т.е.

.

Наконец, это число будет равно 3. Если мы потребуем еще совпадения теоретической и статистической дисперсии:

,

где - статистическое среднее на i-м интервале,

- общее статистическое среднее.

Гипотеза Н₀ отклоняется, если _р²>_кр².

Критерий Пирсона используется при n 100 (хотя бы n 50).