3.3. Производные и дифференциалы высших порядков

Пусть у=f(x) является дифференцируемой в каждой точке интервала (a; b). Тогда в каждой точке этого интервала существует функция – производная от данной (ее называют также первой производной или производной первого порядка функции f(x)). Может случиться, что она так же имеет производную. Тогда эта производная называется второй производной или производной второго порядка функции f(x) и обозначается следующим образом:

.

Подобным образом определяются третья, четвертая и все последующие производные:

.

Определение 3.3.1. Производная от производной порядка n–1 называется производной порядка n и обозначается

.

Аналогично вводится понятие дифференциала n-го порядка.

Определение 3.3.2. Дифференциалом n-го порядка называется дифференциал от дифференциала (n – 1)-го порядка и обозначается:

.

Говорят: дифференциал n-го порядка равен произведению производной n-го порядка на n-ную степень дифференциала независимой переменной.

Отсюда имеем: .

Пример 3.3.1. Для у=sinx получим

и так далее;

, , и так далее.

3.4. Приложения производной

3 .4.1. Геометрический и физический смысл производной и дифференциала

Геометрический смысл производной тесно связан с понятием касательной.

Рассмотрим непрерывную кривую Г – график непрерывной на заданном интервале функции у=f(x) (рис. 3.17). Пусть М(х; у) – лежащая на ней точка и М₁( ), – другая, лежащая на Г точка. Прямую S, проходящую через М и М₁ называют секущей (кривой Г). Если теперь точку М₁ двигать непрерывно по Г, неограниченно приближая к М, тогда секущая S будет вращаться относительно М. Может случиться, что при этом S будет стремиться занять в пределе положение вполне определенной (проходящей через М) прямой. В этом случае говорят, что кривая Г имеет в точке M касательную (на рис. 3.17 – прямая Т). Уравнение касательной к графику функции f(x) в точке М₀(х₀; у₀) имеет вид:

.

Секущая S, проходящая через точки М и М₁, образует с положительным направлением оси Ох угол (рис. 3.17), тангенс которого ( – отношение противолежащего катета к прилежащему в прямоугольном треугольнике ).

Из того, что угол между секущей и касательной при стремлении точки М₁ к точке М, т.е. при уменьшении х до нуля, стремится к нулю, вытекает, что угол перейдет в угол  наклона касательной к оси Ох (рис. 3.17). Тогда получаем

Следовательно, производная функции в точке равна – угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Подчеркнем, что в уравнении касательной к графику функции f(x) в точке М₀(х₀; у₀) также – производная функции в этой точке равна угловому коэффициенту касательной, проведенной к графику функции в точке М₀(х₀; у₀).

Подчеркнем, что уравнение нормали к графику функции f(x) в точке М₀(х₀; у₀) имеет вид:

Г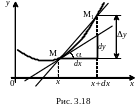 еометрический смысл дифференциала.

Дифференциалом функции у=f(х) первого порядка называется главная, линейная относительно приращения , часть приращения функции , равная произведению производной этой функции на приращение аргумента х, обозначаемое в этом случае, как dx:

dy = = tg dx

Физический смысл производной.

Пусть точка движется прямолинейно по закону s=f(t).

Средняя скорость точки за промежуток времени от t до равна отношению пути , пройденного за этот промежуток времени ко времени движения :

.

Тогда число v, к которому стремиться средняя скорость точки, движущейся прямолинейно по закону s=f(t), на промежутке времени [t, ] при , есть ее скорость или мгновенная скорость в момент времени t:

.

Физический смысл второй производной.

Рассматривая производную скорости по времени t, получим скорость изменения скорости, то есть ускорение.

Таким образом, вторая производная от пути по времени есть ускорение а прямолинейно движущейся точки в момент времени t: .