2.3.2 Определенный интеграл
Теорема Ньютона - Лейбница:
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x) на отрезке [a;b], то имеет место равенство:
Задача Найти
.
Решение:
Свойства определенного интеграла
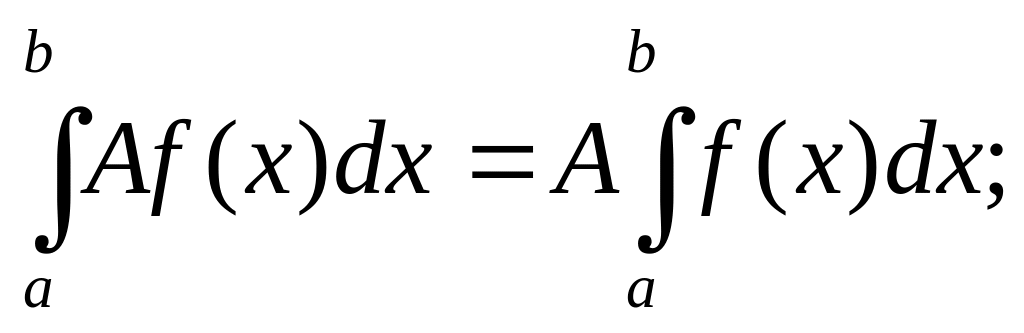
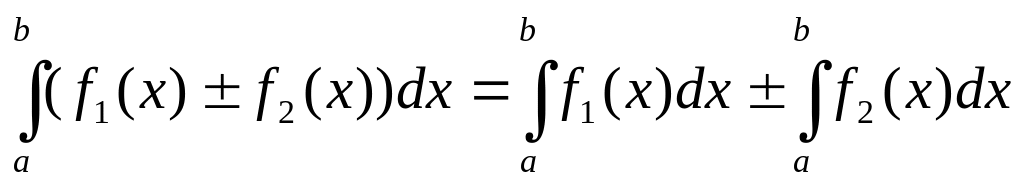
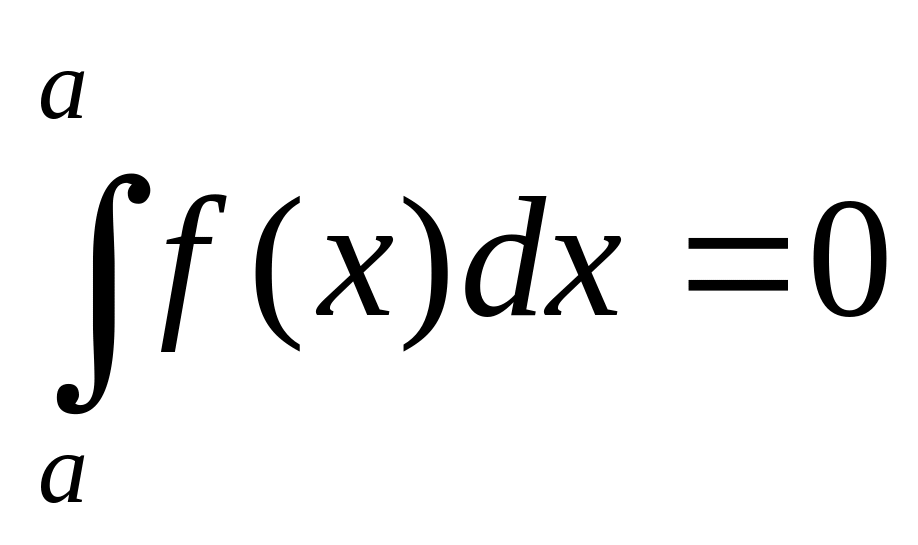
Если f(x) (x) на отрезке [a; b], a<b, то
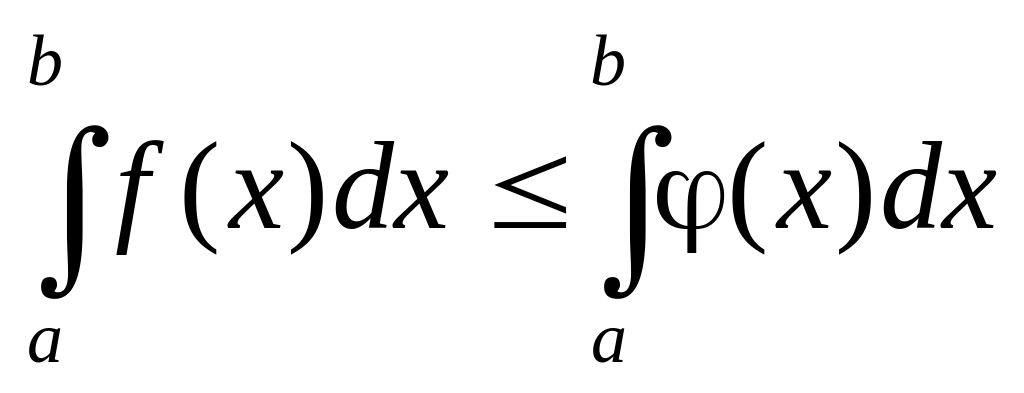
Для произвольных чисел a, b и c, справедливо равенство:
Методы вычисления определенного интеграла
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Особенностью является только то, что при применении этих приемов и методов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
Замена переменной в определенном интеграле
Пусть задан интеграл
,
где f(x)
– непрерывная функция на отрезке [a,
b].
Введем новую переменную в соответствии с формулой x = (t).
Тогда, если
() = а, () = b
(t) и (t) непрерывны на отрезке [, ]
f((t)) определена на отрезке [, ], то
Тогда
Задача:
Вычислите определенный интеграл
Решение: Введем
новую переменную
.
Тогда новые пределы интегрирования
будут равны соответственно: t1=2;
t2=1.
Возведем обе части уравнения замены в квадрат и продифференцируем:
Подставив полученные выражения в исходный интеграл, получим:
При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
2.3.3 Приложения определенного интеграла
1. Вычисление площади плоских фигур
а
)
если
б) если
в)
Задача. Вычислить площадь фигуры, ограниченной параболой y =x2+4x и прямой y =x+4. Сделаем чертеж:
=
=
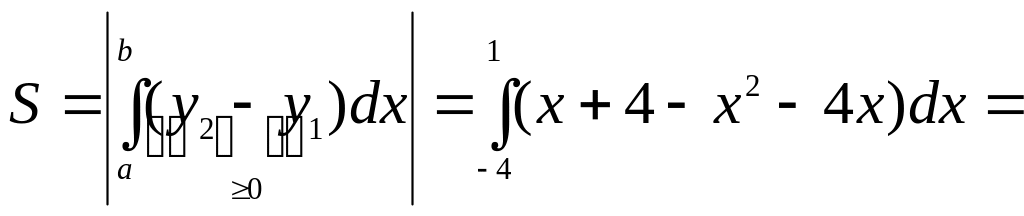
2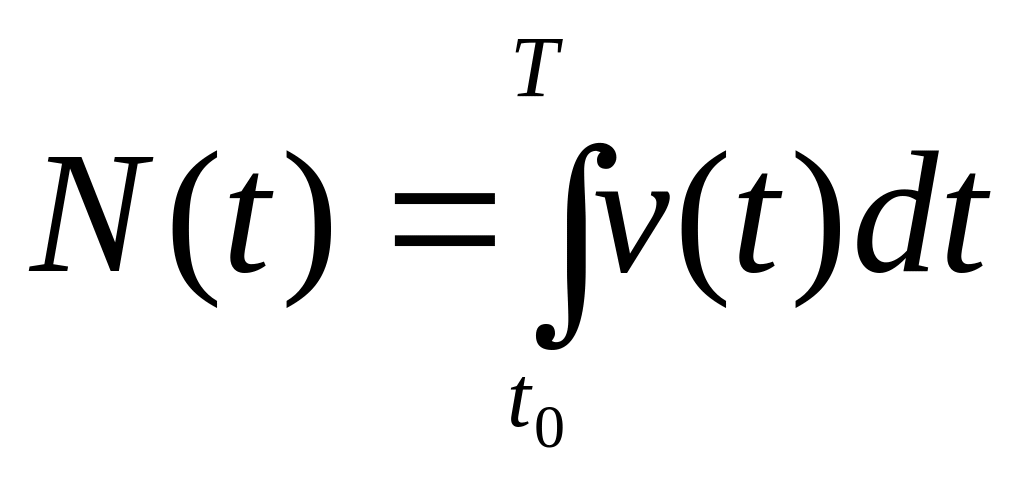
.
Если N(t)
- прирост численности за промежуток
времени от t0
до T,
v(t)
– скорость роста некоторой популяции,
то интеграл от скорости по интервалу
времени ее размножения равен:
3. Одним из наиболее
распространенных приложений определенного
интеграла является решение физически
задач. Если точка движется по некоторой
кривой со скоростью V(t)≥0,
то путь пройденный точкой за время
равен:
Задача:
Скорость точки равна
(м/c).
Найти путь, который точка преодолела
за время t=4c,
прошедшее с начала движения.
Решение:
В нашем случае
.
2.4.4. Интеграл от величины силы по длине пути равен:
Вопросы для самопроверки:
1. Что называется определенным интегралом функции f(x) на отрезке [a;b]?
2.Каковы основные свойства определенного интеграла?
3.Каков геометрический смысл определенного интеграла?
4.Каковы особенности нахождения определенного интеграла с помощью замены переменной?
5.Какие приложения определенного интеграла Вы знаете?