2. Первый и второй законы термодинамики

В основе термодинамики лежат экспериментально установленные законы, которые называют первым и вторым началами термодинамики. С помощью этих законов можно, не делая предположений о молекулярном строении изучаемых тел, получить многие сведения об их свойствах в различных условиях. В то же время молекулярная физика дает возможность связать макроскопические параметры системы с микроскопическими характеристиками вещества.

ОСНОВНЫЕ ФОРМУЛЫ

Первое начало термодинамики: количество теплоты Q, сообщенное системе, идет на увеличение ее внутренней энергии U и совершение системой работы A над окружающими телами:

. (2.1)

Внутренняя энергия идеального газа равна

, (2.2)

где i – число степеней свободы частицы газа, которое равно числу независимых координат, определяющих положение и ориентацию молекулы.

Для одноатомной молекулы газа:	i=3 (поступательные степени свободы).
Для жесткой двухатомной молекулы:	i=5 (3 поступательные и 2 вращательные).
Для жесткой трехатомной молекулы:	i=6 (3 поступательные и 3 вращательные).

Удельная теплоемкость – это скалярная величина, численно равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1^оК,

. (2.3)

Удельная теплота плавления λ, удельная теплота парообразования r, удельная теплота сгорания q – это скалярные величины, численно равные количеству теплоты, необходимому для плавления, парообразования, сгорания, соответственно, 1 кг вещества при соответствующей температуре,

. (2.4)

Удельные теплоемкости газа при постоянном объеме c_V и при постоянном давлении c_p равны

и . (2.5)

Удельная теплоемкость газа, состоящего из n компонент:

. (2.5.1)

Адиабатическим процессом называется термодинамический процесс, осуществляемый без теплообмена с окружающими телами. Уравнение адиабаты (Пуассона) идеального газа

, (2.6)

где показатель адиабаты определяется отношением удельных (или молярных) теплоемкостей:

. (2.6.1) При элементарном расширении газа совершается работа:

, (2.7)

работа при изобарическом процессе:

, (2.7.1)

работа при изотермическом процессе:

, (2.7.2)

работа при адиабатическом процессе:

. (2.7.3)

Энтропия есть функция состояния системы, дифференциал которой при элементарном обратимом процессе равен отношению бесконечно малого количества теплоты, сообщенного системе, к абсолютной температуре последней. При переходе системы из состояния А в состояние В изменение энтропии равно

. (2.8)

Энтропия сложной системы равна сумме энтропий ее однородных частей.

Статистическое определение энтропии (формула Больцмана)

, (2.9)

где k – постоянная Больцмана, W – термодинамическая вероятность, т.е. число способов, которыми можно осуществить данное макроскопическое состояние системы.

Второе начало термодинамики: энтропия замкнутой системы не уменьшается – она возрастает при необратимых процессах или остается постоянной в случае обратимых процессов,

. (2.10)

Изменение энтропии 1 моля идеального газа при переходе из состояния 1 в состояние 2:

. (2.11)

Замечание. В термодинамическом отношении многие системы (включая биологические) являются открытыми, поскольку через свои границы обмениваются веществом и энергией с окружающей средой. Они могут проходить через ряд неравновесных состояний, при которых возможно уменьшение энтропии. Такие процессы называются самоорганизацией системы. Уменьшение энтропии в процессе роста живых систем происходит за счет свободной энергии, освобождаемой при распаде поглощаемых извне питательных веществ или за счет энергии солнца (фотосинтез).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 2.1 Чему равны удельные теплоемкости c_p и c_V некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна ρ₀ = 1.43 кг/м³ ?

Решение. Удельные теплоемкости газа при постоянном объеме и постоянном давлении, согласно формулам (2.4), равны

и .

В этих выражениях нужно определить величины i и M. Для двухатомного газа число степеней свободы i = 5, молярную массу M найдем из уравнения Клапейрона-Менделеева (1.1) и данной в условии плотности газа, ρ₀ = m / V :

.

Подставляя это выражение в формулы для теплоемкостей, получаем

Вычисления проводим, учитывая, что при н.у. p₀ = 1.013∙10⁵ Па, T₀ = 273^оK.

Ответ. c_p = 650 Дж/(кг∙K) , c_V = 908 Дж/(кг∙K)

Пример 2.2 Азот занимает объем V = 2 л под давлением p = 10⁵ Па. Какое количество теплоты надо сообщить азоту, чтобы

а) при p = const объем увеличить вдвое?

б) при V = const давление увеличить вдвое?

Решение. Согласно первому началу термодинамики (2.1), необходимое количество теплоты

.

Найдем изменение внутренней энергии и совершенную работу в обоих случаях.

а) p = const. Согласно формуле (2.2) изменение внутренней энергии

.

Из уравнения состояния (1.1) и условия V₂ = 2V₁ = 2V находим, что

.

Поэтому получаем

.

Cовершенная работа при условии V₂ = 2V₁ = 2V равна

.

Окончательно,

.

б) V = const. Согласно формуле (2.2) изменение внутренней энергии

.

Из уравнения состояния (1.1) и условия p₂ = 2p₁ = 2p находим, что

.

Поэтому также как в предыдущем случае получаем

.

Но в отличие от предыдущего случая, совершенная работа при постоянном объеме A=0. Следовательно, необходимое количество теплоты равно

.

Вычисления проводим, учитывая, что азот – двухатомный газ с числом степеней свободы i = 5 и его объем в единицах СИ равен 1 л = 10^-3 м³.

Ответ. Q_p = 700 Дж , Q_V = 500 Дж.

Пример 2.3 Масса m = 10,5 г азота изотермически расширяется при температуре t = -23^oC от давления p₁ = 2,5 атм до p₂ = 1 атм. Найти работу, совершенную газом при расширении.

Решение. По определению (2.7), работа, совершенная газом при расширении, равна

.

В общем случае давление зависит от изменения объема. Эту зависимость можно найти из уравнения состояния (1.1), а именно,

,

причем для изотермического процесса T = const, поэтому имеем

.

В этом выражении нам неизвестно отношение V₂/V₁, которое можно найти с помощью закона Бойля-Мариотта V₂/V₁ = p₁/p₂ , следовательно

.

Подставим численные значения, учитывая, что абсолютная температура процесса T = -23+273 = 250^оK, и молярная масса азота M= 28 г/моль.

Ответ. A = 720 Дж.

Пример 2.4 Газ расширяется адиабатически, при этом его объем увеличивается вдвое, а абсолютная температура падает в 1,32 раза. Какое число степеней свободы имеют молекулы данного газа?

Решение. Так как масса газа не изменяется, то согласно уравнению адиабаты (2.6) для газа в начале и в конце процесса, имеем:

.

Чтобы выразить неизвестные давления через температуры газа в начале и в конце процесса, воспользуемся уравнением состояния (1.1) в виде:

.

Отсюда следует, что

.

С учетом предыдущего, получаем: . Возьмем логарифм левой и правой частей этого равенства, отсюда находим

.

Принимая во внимание связь показателя адиабаты с числом степеней свободы молекул газа (2.6.1), γ= c_p/c_V = (i + 2)/i , окончательно получаем

.

Осталось провести вычисления, используя условия задачи:

Ответ. Число степеней свободы данного газа i = 5, следовательно, газ двухатомный.

Пример 2.5 Двухатомный газ, находящийся при температуре t₁=27^оC и давлении p₁ = 2∙10⁶ Па сжимается адиабатически от объема V₁ до объема V₂ = 0,5V₁. Найти температуру t₂ и давление p₂ газа после сжатия.

Решение. Поскольку газ двухатомный, то число степеней свободы его частицы i = 5, а показатель адиабаты γ=(i+2)/i = 7/5 = 1,4. Тогда давление после сжатия можно сразу же найти из уравнения адиабаты (2.6):

, отсюда .

Чтобы найти температуру после сжатия, воспользуемся уравнением состояния (1.1)

, отсюда

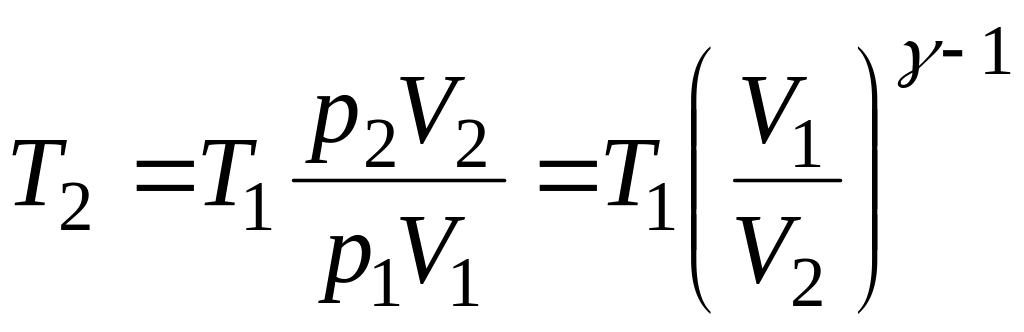
Подставляем численные значения, учитывая, что T₁ = 27 + 273 = 300^оK.

Ответ. t₂ = 123^оC; p₂ = 52,8∙10⁵ Па.

Пример 2.6 Найти изменение энтропии при превращении m = 10 г льда при t₁ = -20^oC в пар при t₂ = 100^oC. Удельная теплоемкость льда c_i=2,1∙10³ Дж/(кг∙К), удельная теплоемкость воды c_h=4,2∙10³ Дж/(кг∙К), удельная теплота плавления λ=3,35∙10⁵ Дж/кг, удельная теплота парообразования r=2,26∙10⁶ Дж/кг.

Решение. По определению (2.8), изменение энтропии равно

.

Рассматриваемый сложный процесс состоит из четырех этапов: (1) нагревание льда, (2) плавление льда, (3) нагревание воды, (4) парообразование. На каждом этапе переданное количество теплоты идет на увеличение внутренней энергии или на преобразование структуры вещества.

Изменение энтропии на этапе нагревания льда до температуры плавления t₂= 0^oC ( T₂ = 273^oK), с учетом (2.3) , составит

,

в процессе плавления льда, с учетом определения (2.4):

,

на этапе нагревания воды до температуры кипения T₃ = 373^oK :

,

в процессе кипения воды:

.

Полное изменение энтропии равно сумме

.

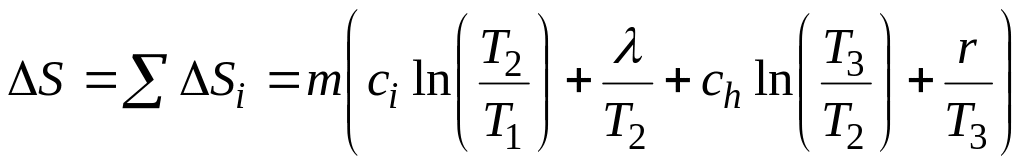После подстановки значений получаем ответ.

Ответ. Изменение энтропии равно ΔS = 88 Дж/К .

Пример 2.7 Азот массой m = 10,5 г изотермически расширяется от объема V₁= 2 л до объема V₂= 5 л. Найти изменение энтропии в этом процессе.

Решение. По определению, изменение энтропии равно

Так как в изотермическом процессе температура не изменяется, то dU= 0, поэтому dQ=δA=pdV. Из уравнения состояния (1.1) выразим давление , подставим в формулу для изменения энтропии и проинтегрируем:

.

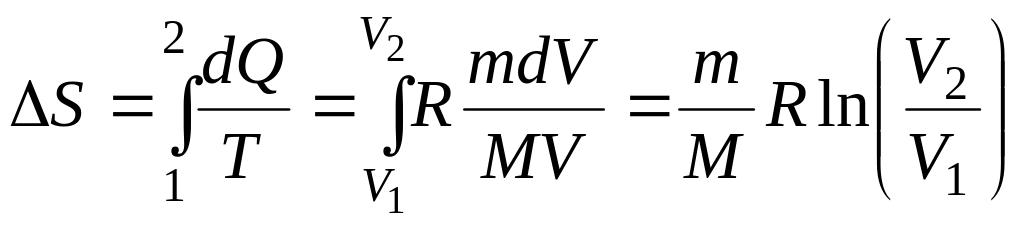После подстановки значений, учитывая, что молярная масса азота M=28 г/моль, получаем ответ.

Ответ. Изменение энтропии равно ΔS = 2,85 Дж/К.

Пример 2.8 При нагревании ν = 1 кмоль двухатомного газа его абсолютная температура увеличивается в 1,5 раза. Найти изменение энтропии при: 1) изохорном нагревании и 2) при изобарном нагревании газа.

Решение. По определению, изменение энтропии равно

.

При изохорном нагревании работа не совершается, δA = pdV = 0. Изменение внутренней энергии dU = (m/M)(i/2)RdT , поэтому

.

При изобарном процессе совершается работа δA = pdV = (m/M)RTdV/V . Изменение внутренней энергии dU = (m/M)(i/2)RdT , поэтому

.

В этом выражении нам неизвестно отношение объемов V₂/V₁ . Его можно найти по закону Гей-Люссака: V₂/V₁ = T₂/T₁. Отсюда получаем

.

Подставляем численные значения, учитывая, что в условии задачи дано число молей ν=m/M, T₂/T₁ = 1,5 и число степеней свободы двухатомного газа i = 5.

Ответ. ΔS_V = 8,42∙10³ Дж/К, ΔS_p = 11,8∙10³Дж/К

Пример 2.8 Кислород массой 1 кг занимает объем V₁ . Определить вероятность самопроизвольного изотермического сжатия кислорода на 10^-6 часть первоначального объема.

Решение. Пусть W₁ – вероятность того, что кислород занимает объем V₁, W₂ – вероятность того, что после самопроизвольного изотермического сжатия его объем V₂. Изменение энтропии согласно формуле Больцмана (2.9) равно

.

С другой стороны, при изотермическом изменении объема

.

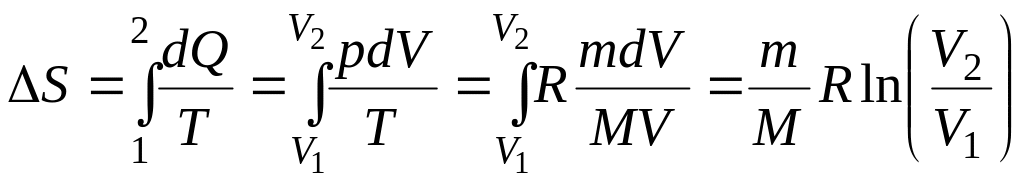Приравнивая правые части этих выражений, получим

.

Следовательно,

.

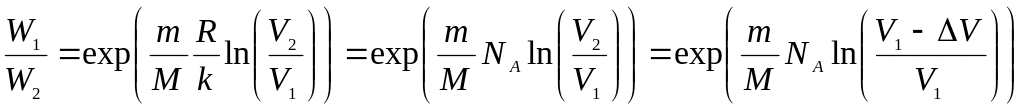Подставим заданные числовые значения и учтем, что при малых х=ΔV/V₁. Получим .

Ответ. Вероятность самопроизвольного изотермического сжатия газа практически равна нулю.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

11. Найти удельные теплоемкости c_p и c_V некоторого двухатомного газа, если известно, что его молярная масса равна M=30 г/моль³ и отношение c_p/c_V=1,4 .

12. Азот находится в закрытом сосуде объемом V = 3 л при температуре t = 27^oC и давлении p = 3 атм. После нагревания давление в сосуде повысилось до p = 25 атм. Определить температуру азота после нагревания и количество теплоты, переданное газу.

13. Для нагревания некоторого количества газа на Δt = 50^оC при постоянном давлении необходимо затратить Q₁ = 672 Дж теплоты. Если это же количество газа охладить на Δt = 100^оC при постоянном объеме, то выделится Q₂ = 1008 Дж теплоты. Какое количество степеней свободы имеют молекулы этого газа?

14. В сосуде под поршнем находится m = 1 г азота. Какое количество теплоты надо затратить, чтобы нагреть азот на Δt = 10^оC ? На сколько при этом поднимется поршень, если его масса M = 1 кг, а площадь поперечного сечения S = 10 см² ? Атмосферное давление p=10⁵ Па.

15. Газ расширяется адиабатически так, что его давление падает от p₁ = 2 атм до p₂ = 1 атм. Затем он нагревается при постоянном объеме до первоначальной температуры, причем его давление возрастает до p₃=1,22атм. Определить отношение c_p/c_V для этого газа. Начертить график этого процесса.

16. Определить, какую энергию затратит организм человека при испарении пота с поверхности тела, если известно, что за сутки выделяется 0,5 л пота. На испарение 1 кг пота при температуре 34^оС требуется 24,4·10⁵ Дж. Плотность пота принять равной 1,2·10³ кг/м³.

17. Соревнования по «банному» спорту проходят в финских банях, где температура достигает 120^оС, т.е. при температуре значительно выше кипения воды. Более того, доказано, что человек может некоторое время находиться в помещении с температурой воздуха до 160^оС. Почему это возможно? Где труднее переносится сильная жара: во влажном климате или в сухом климате?

18. Какой термометр более чувствительный: ртутный или спиртовой (при прочих равных условиях)? Почему в медицинских термометрах используют ртуть, а не спирт?

19. Можно ли обычным ртутным термометром измерить температуру одной капли горячей воды?

20. Можно ли охладить комнату, оставив открытой дверь холодильника?

21. Найти изменение энтропии при плавлении m = 10г свинца, взятого при температуре t₁ = 27^oC . Температура плавления свинца t_пл = 327^oC , удельная теплоемкость свинца c = 126 Дж/(кг∙К), удельная теплота плавления λ = 22,6 кДж/кг.

22. Найти изменение энтропии при переходе m = 8г кислорода от объема V₁ = 10 л при температуре t₁ = 80^oC к объему V₂ = 40 л при температуре t₂ = 300^oC.

23. Найти изменение энтропии при переходе m = 6г водорода от объема V₁ = 20л при давлении p₁=1,5∙10⁵ Па к объему V₂ = 60 л при давлении p₂=10⁵Па.

24. В двух сосудах одного и того же объема находятся различные идеальные газы массой m₁ и m₂, соответственно. Давления и температуры газов одинаковы. Сосуды соединяют и начинается процесс диффузии. Определить изменение энтропии системы, если молярные массы газов равны M₁ и M₂, соответственно. Указание. Процесс диффузии можно рассматривать как изотермическое расширение газов от объема V₁ до объема V₂= 2V₁ .

25. Исходя из второго закона термодинамики Клаузиус (1822-1888) выдвинул тезис о «тепловой смерти Вселенной»: поскольку со временем установится тепловое равновесие, то прекратятся всякие тепловые явления, в том числе исчезнет и жизнь. Ошибался ли Клаузиус?