3. Теоретические положения по организации моделирования транспортных сетей

3.1 Задача поиска кратчайшего пути (наименьшей длины)

Задачу поиска кратчайшего пути между источником и стоком (начальный и конечный пункты сети) можно решить с помощью алгоритма Дейкстры. Алгоритм Дейкстры разработан для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети.

В процессе выполнения этого алгоритма при переходе от узла до следующего узла используется специальная процедура отметки ребер. обозначим через кратчайшее расстояние от исходного узла 1 до узла , через – длину ребра . Тогда для узла определим метку таким образом:

Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный.

Расчетная схема алгоритма состоит из следующих шагов.

Шаг 0. Выходному узлу (узел 1) присваивается метка . Думаем .

Шаг i. а) Вычисляются временные метки для всех узлов , которые можно достичь непосредственно из узла , и какие имеют постоянные метки. Если узел уже имеет метку , полученную от другого узла , и если , тогда метка заменяется на .

б) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка с наименьшим значением расстояние всех временных меток (если таких меток несколько, то выбор в-свободный). Думаем и повторяем шаг .

3.2. Задача определения кратчайших расстояний между элементами транспортной сети (Алгоритм Флойда).

Данная задача решается с помощью алгоритма Флойда.

Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, потому что он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с строками и столбиками. Элемент равна расстоянию от узла до узла , что конечное значение, если существует дуга , и равна бесконечности в противном случае.

Покажем сначала основную идею метода Флойда Пусть имеется три узла и заданные расстояния между ними (рис. 3.1). Если выполняется неравенство с , то целесообразно заменить путь , то путем . Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

Рис. 3.1. Треугольный оператор

Алгоритм Флойда требует выполнения следующих действий.

Шаг 0. Определяем начальную матрицу расстояний и матрицу последовательности узлов . Диагональные элементы обеих матриц обозначаются знаком "-", что показывает, что эти элементы в вычислениях не участвуют. Думаем :

Рис.3.2. Начальная ситуация

Основной шаг k. Задаем строку и столбец как ведущий строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементов матрицы . Если выполняется неравенство , тогда выполняем следующие действия:

• создаем матрицу путем замены в матрице элемента на сумму ,

• создаем матрицу 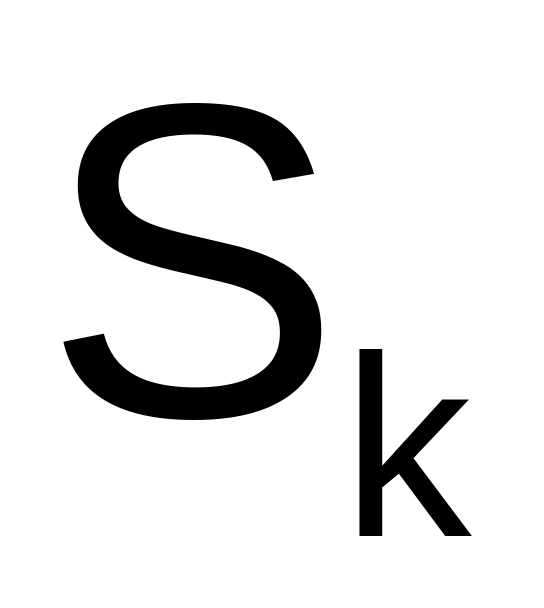путем замены в матрице 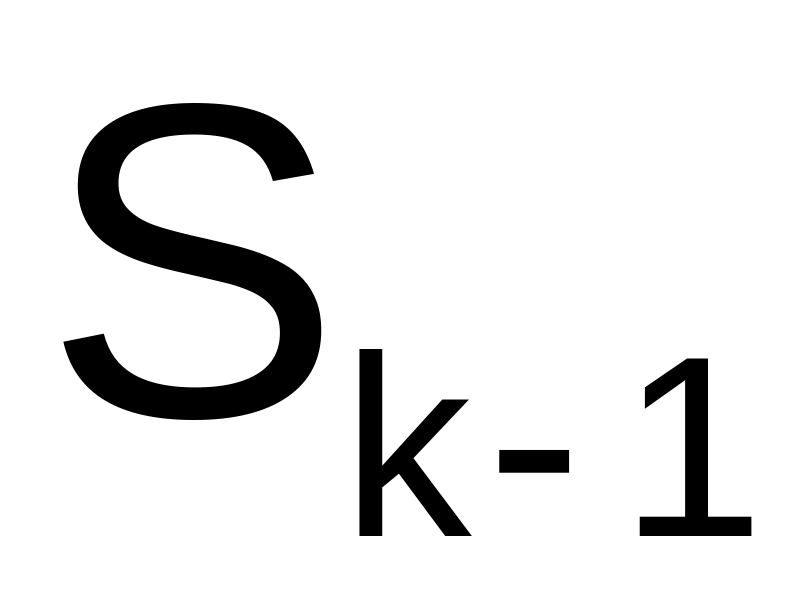элемента на . Думаем 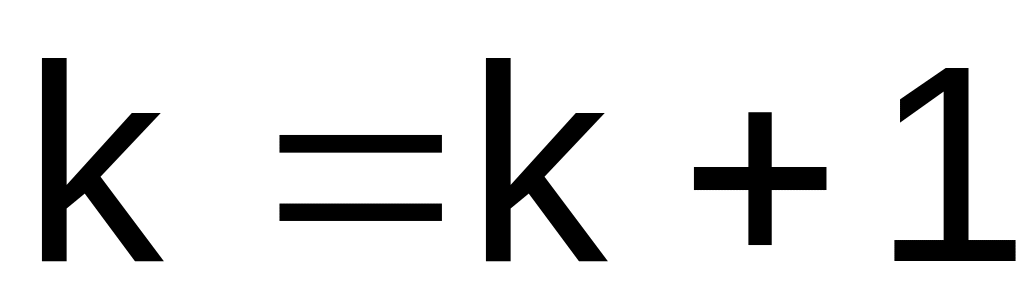и повторяем шаг .

Поясним действия, выполняемые на -м шаге алгоритма, представив матрицу так, как она показана на рис 3.3. На этом рисунке строка и столбец являются ведущими. Строка - любая строка с номером от 1 до , а строка - произвольный строку с номером от до . Аналогично столбец представляет любую столбец с номером от 1 до , столбец - произвольный столбец с номером от до . Треугольный оператор выполняется следующим образом. Если сумма элементов ведущих строки и столбца (показанных в квадратах) меньше элементов, находящихся в пересечении столбца и строки (показанных в кружках), соответствующие рассмотренным ведущим элементам, то расстояние (элемент в кружке) заменяется на сумму расстояний, представленных ведущими элементами:

Рис.3.3. Иллюстрация алгоритма Флойда

После реализации шагов алгоритма определения по матрицам и кратчайшему пути между узлами и выполняется по следующим правилам.

1. Расстояние между узлами и равна элементу в матрице .

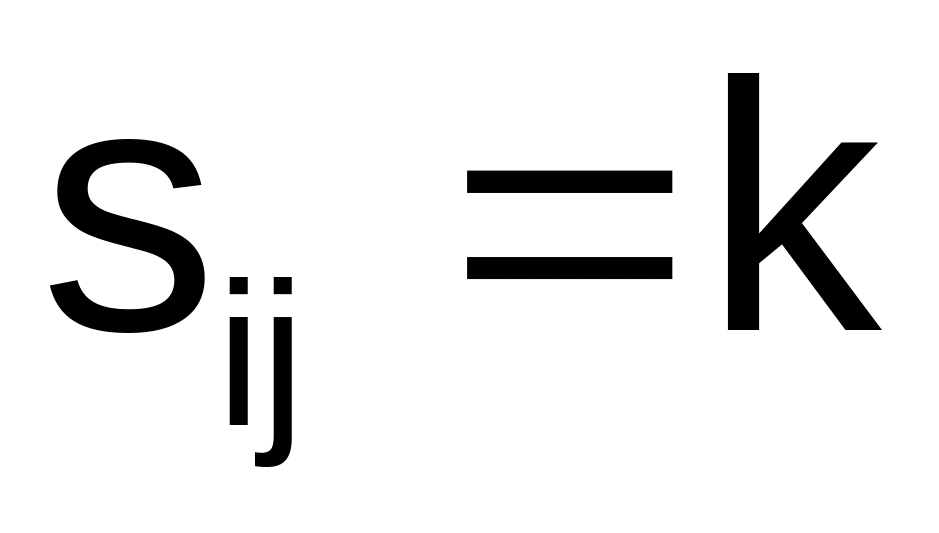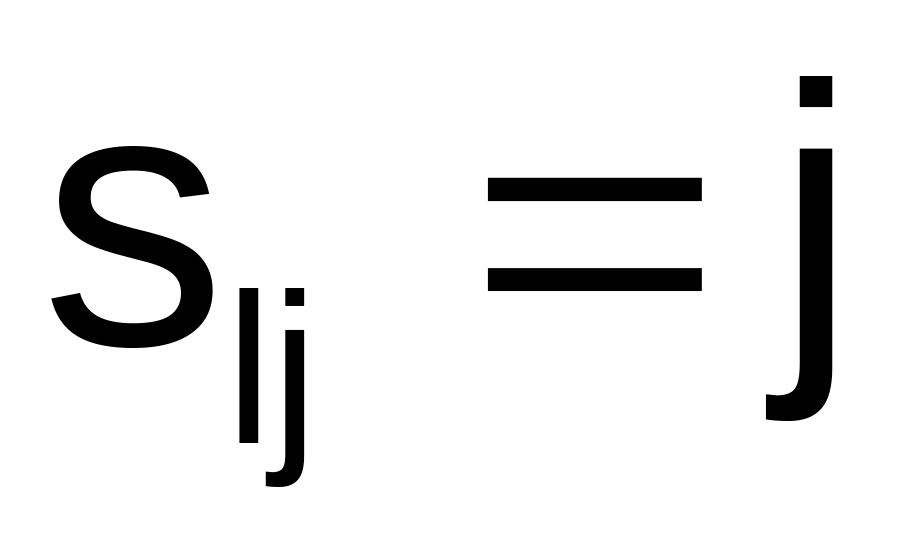2. Промежуточные узлы пути от узла к узлу определяем по матрице . Пусть , тогда имеем путь . Если дальше и , тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла к узлу и от узла к узлу .