Практическое занятие №11

Наименование занятия: Векторы в пространстве

Цель занятия: Научиться находить двугранные углы, использовать теоремы перпендикулярности плоскостей в решении задач.

Подготовка к занятию: Повторить теоретический материал по теме «Векторы в пространстве»

Литература:

1. Атанасян Л.С. и др. «Геометрия 10-11»

2. Дадаян а.А. «Математика»

Задание на занятие:

1. Дан параллелепипед ABCDA₁B₁C₁D₁. ABCD – прямоугольник, E и F – середины ребер В₁С₁ и C₁D₁ соответственно. Запишите векторы с началом и концом в вершинах параллелепипеда, которые:

1. сонапарвлены с вектором

2. противоположно направлены вектору

3. имеют длину, равную длине вектора

2. ABCDA₁B₁C₁D₁ – параллелепипед. Укажите вектор, равный сумме векторов . Докажите, что векторы и 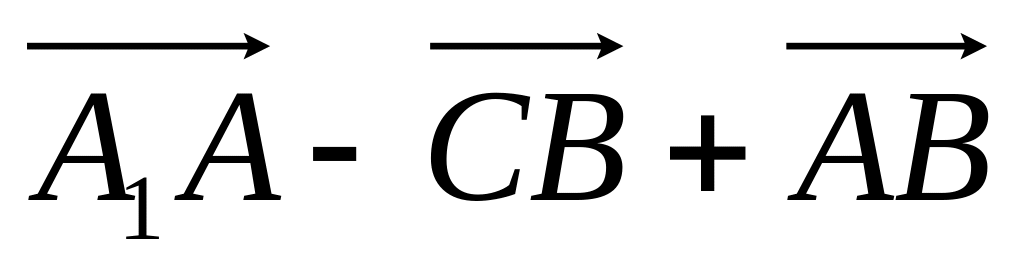противоположны.

3. Нарисуйте параллелепипед ABCDA₁B₁C₁D₁ и обозначьте векторы , , соответственно через , 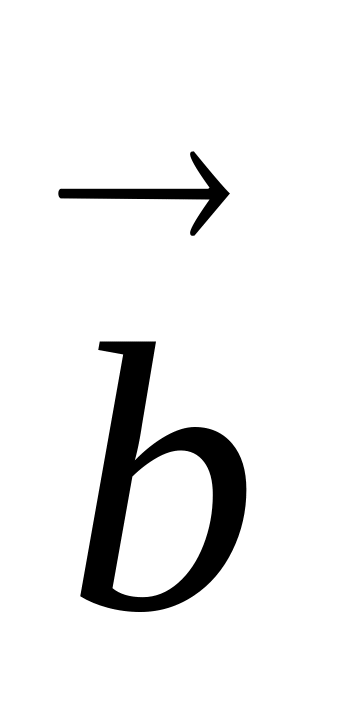и . Изобразите на рисунке векторы , , , , .

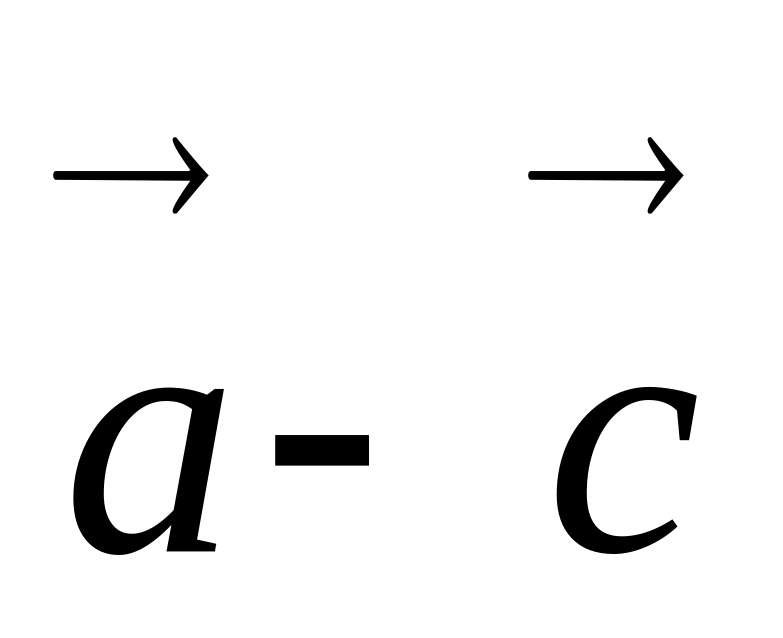Порядок проведения занятия:

1. Получить допуск к работе;

2. Выполнить задания;

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется вектором?

2. Какие векторы называются коллинеарными? Сонаправленными? Противоположно направленными?

3. Что называется суммой, разностью векторов, произведением вектора на число?

Практическое занятие №12

Наименование занятия: Координаты вектора в пространстве. Простейшие задачи в координатах

Цель занятия: Научиться находить координаты вектора, решать простейшие задачи в координатах

Подготовка к занятию: Повторить теоретический материал по теме «Координаты вектора в пространстве»

Литература:

1. Атанасян Л.С. и др. «Геометрия 10-11»

2. Дадаян а.А. «Математика»

Задание на занятие:

1. Даны векторы {-1; 2; 0}, {0; -5; 2}, {2; 1; -3}. Запишите разложения этих векторов по координатным векторам , 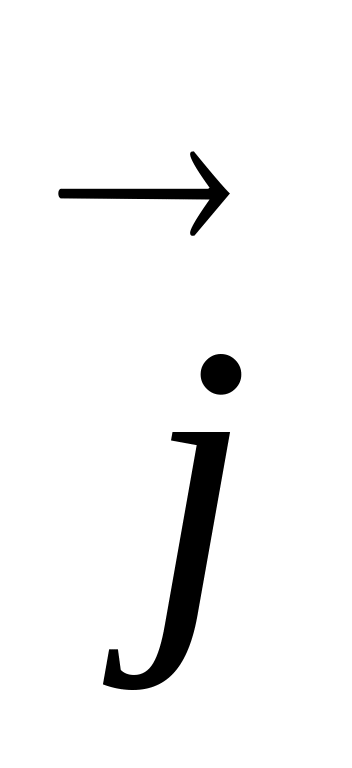и .

2. Даны векторы {3; -5; 2}, {0; 7; -1}, . Найти координаты векторов , , , , .

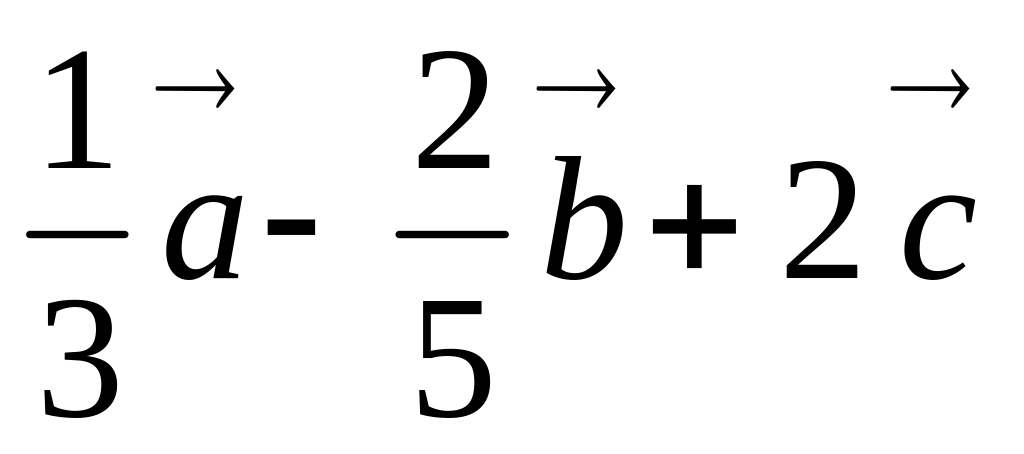3. Найти координаты вектора 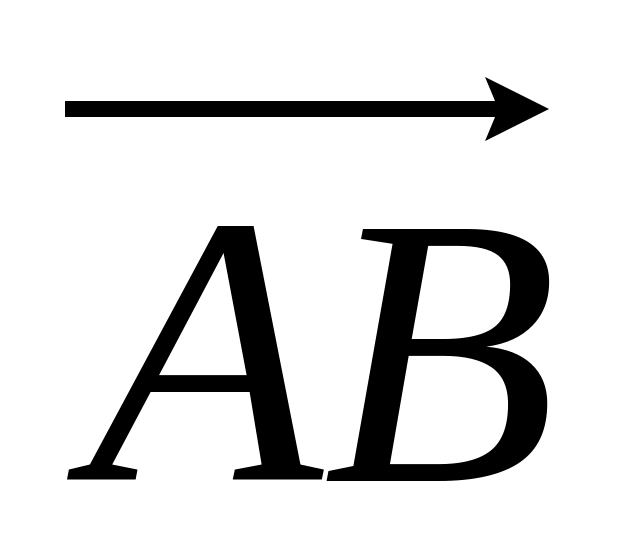, если а) А(-2; 6; -2), В(3; -1; 0)

б) А , В

4. Найти длины векторов , = -2 , = +2 -2 .

5. Даны векторы {3; -2; 1}, {-2; 3; 1}, {-3; 2; 1}. Найти , ,

6. Найти длину вектора , если А(-1; 0; 2), В(1; -2; 3)

Порядок проведения занятия:

1. Получить допуск к работе;

2. Выполнить задания;

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется координатными векторами? Как разложить произвольный вектор по координатным векторам?

2. Как найти длину вектора, если известны его координаты? Координаты точек начала и конца вектора?