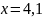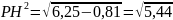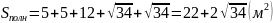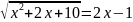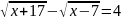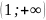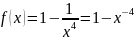2. Решите неравенство:

Решение. Подкоренное выражение, как известно, не может принимать отрицательных значений, также не допускается нахождение в знаменателе дроби нуля. Следовательно, область допустимых значений данного неравенства определяется неравенством   и тем условием, что   Решаем уравнения   и   Из первого уравнения получаем, что   Из второго уравнения получаем, что   Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений   и   не удовлетворяет неравенству. Сразу определяем знаки выражения   в каждом из полученных промежутков и рисуем кривую знаков:

Верхней стрелкой на рисунке обозначена область допустимых значений неравенства. Ответом к неравенству будет являться промежуток, соответствующий на рисунке заштрихованной области.

Ответ: 

Приложение к практическому занятию № 23.

Решить иррациональные уравнения:

1. 

Возведём обе части уравнения в квадрат:

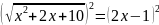
Сделаем проверку. Подставим полученные корни в уравнение:

При

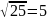– верное равенство

При

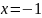
- не верное равенство

:

2. 

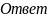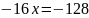
Сделаем замену переменной:

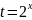
Заметим, что . Поэтому данное уравнение принимает вид:

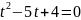
Найдём решения этого квадратного уравнения: 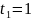и .

Решая уравнения 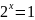и , получаем и .

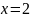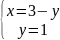
Ответ:

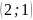
Приложение к практическому занятию №29.

Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называются критическими точками этой функции.

Если в точке производная меняет знак с плюса на минус, то есть точка максимума.

Если в точке производная меняет знак с минуса на плюс, то есть точка минимума.

Пример: найти точки минимума и максимума функции

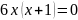
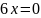или

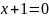
или

Отметим точки на числовой прямой и определим знак производной в каждом из полученных интервалов.

- точка максимум

- точка минимум

Наибольшее и наименьшее значение функции

Чтобы найти наибольшее и наименьшее значение функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках, а затем из полученных чисел выбрать наибольшее и наименьшее.

Пример: найти наибольшее и наименьшее значение функции

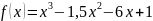на отрезке

Найдём критические точки. Так как производная определена для любого значения переменной, остаётся решить уравнение

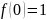
Критическая точка не принадлежит рассматриваемому промежутку.

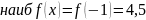
План исследования функции:

1. Область определения

2. Четность – нечётность функции; периодичность

3. Точки пересечения графика с осями координат

4. Промежутки знакопостоянства

5. Промежутки возрастания и убывания функции

6. Точки эктсремума и значения функции в этих точках

7. График

Пример: исследовать функцию и построить её график

1. 

2. 

Функция ни чётная ни нечётная; не периодическая

3. Точки пересечения с осью OX:

Уравнение не имеет корней, следовательно нет точек пересечения с осью OX.

Точки пересечения с осью OY:

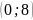
4. на всей области определения

5. 

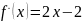
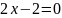
6. - точка минимума

	-	0	+
	убывает	8	возрастает
		min

Приложение к практическому занятию № 30.

Функция называется первообразной для функции на заданном промежутке, если для всех из этого промежутка

Любая первообразная для функции на заданном промежутке может быть записана в виде:

- общий вид первообразной.

Таблица первообразных

Функция f	k
Общий вид первообразной

Пример:

Найти общий вид первообразной:

1. 

2. 

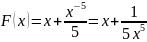
Найти для функции первообразную, график которой проходит через точку M.

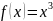
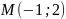
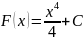
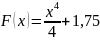
Площадь фигуры, ограниченной кривой , где 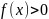, осью ОХ и двумя прямыми и , выражается определённым интегралом:

Пример:

1. Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение:

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу , найдем пределы интегрирования. Для этого решим систему двух уравнений:

Таким образом, имеем х = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = 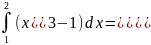(кв.ед)

Ответ:

2. Вычислить площадь фигуры, ограниченной линиями ; у = 2; х = 9.

Решение:

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

, а снизу графиком функции . Полученная фигура показана штриховкой на рис. 3. Искомая площадь равна . Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, (кв.ед)

Ответ: (кв.ед.)

3. Вычислить площадь фигуры, ограниченной линиями  ;

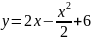
Решение:

Находим точки пересечения заданных линий. Для этого решаем систему уравнений:

Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:

    или     .

Находим: x₁ = -2, x₂ = 4.

Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).

Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:

По формуле Ньютона-Лейбница находим:

Приложение к практическому занятию № 31.

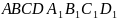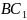1. Найдите объем прямоугольного параллелепипеда , если = 13 см, BD= 12 см и = 11 см.

Обозначим стороны АВ=а, ВС=b и СС₁=с. Тогда условия выглядят так:

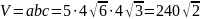
Ответ: (

2. Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30° с плоскостью боковой грани и угол в 45° с боковым ребром. Найдите объем параллелепипеда.

BC₁ — проекция D₁B на плоскость боковой грани ВВ₁С₁С, поэтому ∠D₁BC₁=30°, ∠DBB₁=45°.

Вычислим — из прямоугольного ΔD₁C₁B: D₁C₁ = 9 см, как катет лежащий против угла в 30°. Из прямоугольного

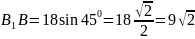
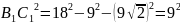
Ответ:

3. В цилиндр вписана призма, основанием которой является прямоугольный треугольник с катетом а и прилежащим к нему углом α. Найдите объем цилиндра, если высота призмы равна h.

∠С=90°. ∠АСВ — вписанный и равен 90°, тогда, АВ — диаметр.

r — радиус основания цилиндра.

Высота призмы равна высоте цилиндра, значит,

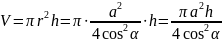
Приложение к практическому занятию №32.

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.

Пример: решить уравнение

Выполнить действия:

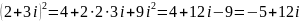
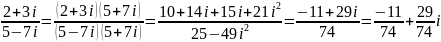
Каждой точке плоскости с координатами соответствует один и только один вектор с началом O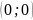 и концом Z . Поэтому комплексное число можно изобразить в виде вектора с началом O и концом Z .

Изобразить на плоскости числа: ; ; ; ;

Приложение к практическому занятию №33.

Три формы записи комплексного числа:

1. – алгебраическая

2. - тригонометрическая

3. - показательная

Записать число в показательной и тригонометрической формах .

,

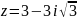Геометрически определяем, что числу соответствует точка Z, лежащая в четвёртой четверти.

Или

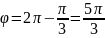
- тригонометрическая форма

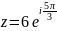- показательная форма.

Выполнить действие и записать результат в тригонометрической форме:

,

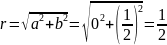
Приложение к практическому занятию № 34.

1. Перестановки – комбинации из n элементов, которые отличаются друг от друга только порядком элементов.

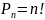
Сколько различных пятизначных чисел можно составить из чисел 1,2,3,4,5 при условии, что ни одна цифра в числе не повторяется?

Ответ: 120 чисел

2. Размещения – комбинации из m элементов по n, которые отличаются друг от друга или самими элементами или порядком элементов.

Сколько существует вариантов размещения трёх призовых мест, если в розыгрыше участвует 7 команд?

Ответ: 210 вариантов

3. Сочетания – все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним из элементов.

Сколькими способами можно выбрать трёх дежурных, если в классе 30 учащихся?

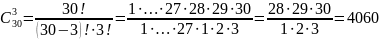
Ответ: 4060 способами

Сколькими способами можно составить дозор из трёх солдат и одного офицера, если имеется 80 солдат и 3 офицера?

Ответ: 246480 способами

Приложение к практическому занятию №35.

Вероятность события А равно отношению числа m исходов испытаний, благоприятствующих событию А, к общему числу n всех равновозможных несовместных исходов, т.е.

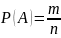
Примеры:

1. Найти вероятность того, что наугад выбранное целое число от 0 до 60 делится на 60.

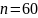
2. В классе 17 девочек и 14 мальчиков. Определить вероятность того, что оба вызванных ученика окажутся: а) мальчиками б) девочками

1. 

2. 

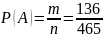
Приложение к практическому занятию №26.

1. Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60°. Меньшая из площадей диагональных сечений равна 130 . Найдите площадь поверхности параллелепипеда.

Сечение параллелепипеда называется диагональным, если оно содержит какую-нибудь его диагональ и боковое ребро.

Решение: пусть ,

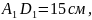
Пусть боковое ребро равно Н, тогда площадь первого диагонального сечения S₁ = H BD, а площадь второго S₂ = Н АС;

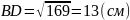
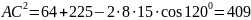
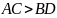
Наименьшее сечение

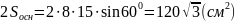
Ответ:

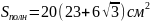
2. Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды.

Решение:

Пусть АВ = 5 м, АD = 4 м, BD = Зм и PO = 2 м. Заметим, что АВ² = AD² + BD² и значит ∠BDA = 90°. Но OD — проекция PD на плоскость ABCD. Поэтому PD⊥AD.

Аналогично PB⊥ВС. Найдем PD:

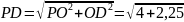
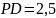
Аналогично .

Аналогично .

Найдем S_PAB и S_PDC: так как ΔPAB=ΔPDC ( по трем сторонам), то достаточно найти площадь одного из треугольников. Рассмотрим ΔPDC: проведем высоту PH

Пусть CH = x, тогда