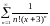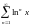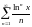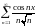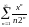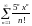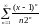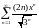- •§1 Числовые ряды. Основные понятия.
- •Задачи для самостоятельного решения
- •§2. Достаточные признаки сходимости знакоположительных рядов.
- •Задачи для самостоятельного решения
- •§3 Абсолютная и условная сходимость.
- •Задачи для самостоятельного решения
- •§4 Функциональные ряды.
- •Задачи для самостоятельного решения
- •§5 Ряды Фурье.
- •Задачи для самостоятельного решения
- •Список литературы
Задачи для самостоятельного решения
Найти область сходимости данных рядов:
Разложить функцию
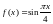 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки
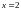
Найти первые пять членов ряда Тейлора для функции
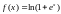 в окрестности точки
в окрестности точки
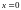
Разложить функции в ряд Маклорена:
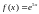 ;
;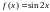 ;
;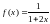 ;
;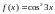 .
.
Разложить функции в ряд Тейлора:
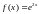 по степеням
по степеням
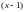 ;
;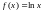 по степеням
;
по степеням
;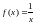 по степеням
по степеням
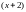 .
.
Вычислить приближенно:
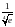 с точностью до
с точностью до
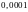
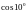 с точностью до
с точностью до
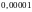
 с точностью до
с точностью до

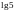 с точностью до
с точностью до
 ,
взять 3 члена разложения, указать
погрешность
,
взять 3 члена разложения, указать
погрешность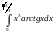 ,
взять 2 члена разложения, указать
погрешность
,
взять 2 члена разложения, указать
погрешность
Ответы:
1) расходится;
2) сходится абсолютно при
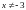 ;
3) сходится абсолютно при
;
3) сходится абсолютно при
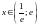 ;
4) сходится при
;
4) сходится при
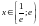 ;
5)
;
5)
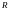 ;
6)
;
6)
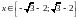 ;
7)
;
7)
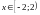 ;
8)
;
9)
;
10)
;
8)
;
9)
;
10)
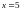 ;
;
11)
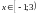 ;
12)
;
12)
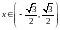 ;
13)
;
13)
 ;
14)
;
14)
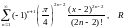 ;
;
15)
 ;
16)
;
16)
 ;
17)
;
17)
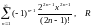 ;
;
18)
 ;
19)
;
19)
 ;
20)
;
20)
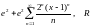 ;
;
21)
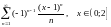 ;
22)
;
22)
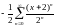 ;
23) 0,7788; 24) 0,17365; 25) 4,121; 26) 0,699; 27) 0,323,
погрешность 0,0001; 28) 0,012, погрешность
0,001.
;
23) 0,7788; 24) 0,17365; 25) 4,121; 26) 0,699; 27) 0,323,
погрешность 0,0001; 28) 0,012, погрешность
0,001.
§5 Ряды Фурье.
Пример
1.
Разложить функцию
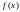 в ряд Фурье и построить график суммы.
в ряд Фурье и построить график суммы.
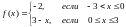
Решение:
Данная
функция терпит разрыв 1 рода в точке
.
Функция удовлетворяет условиям теоремы
Дирихле. В данной задаче период
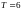 ,
а
,
а
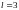 .
.
Разложим функцию в ряд Фурье:
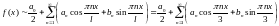
Вычислим коэффициенты ряда. Поскольку функция разрывна в начале координат, то каждый коэффициент Фурье очевидным образом следует записать в виде суммы двух интегралов:
1) Первый интеграл:
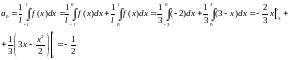 2)
Второй интеграл:
2)
Второй интеграл:
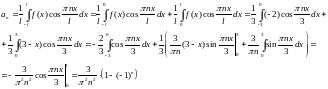 3)
Третий интеграл:
3)
Третий интеграл:
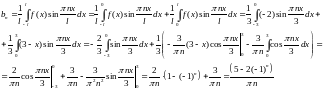 Подставим
найденные коэффициенты Фурье
в
формулу:
Подставим
найденные коэффициенты Фурье
в
формулу:
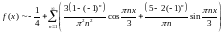 .
.
Полученный
ряд Фурье сходится во всех точках
отрезка
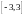 и его сумма
и его сумма
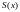 равна:
равна:
1) самой функции в точках непрерывности функции,
2)
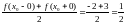 в точке разрыва
в точке разрыва
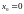 ,
,
3)
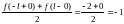 на концах отрезка
на концах отрезка
Построим
график суммы ряда
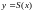 .
На интервале
.
На интервале
 строим
прямую
строим
прямую
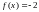 ,
а на интервале
,
а на интервале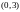 —
прямую
—
прямую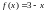 .
В
точке разрыва
—
.
В
точке разрыва
—
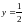 ,
при
,
при
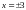 —
—
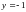 .
И
«продолжаем» график на всю числовую
ось с периодом
.
И
«продолжаем» график на всю числовую
ось с периодом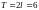 :
:

Пример 2.
Разложить функцию
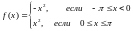 в ряд Фурье.
в ряд Фурье.
Решение:
Наша функция
удовлетворяет условиям теоремы Дирихле.
В данной задаче период
 ,
а
,
а
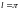 .
Заметим, что функция является
нечетной. Поэтому будем раскладывать
ее в ряд по синусам:
.
Заметим, что функция является
нечетной. Поэтому будем раскладывать
ее в ряд по синусам:
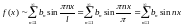 ,
,
где
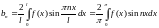 .
.
Вычислим коэффициенты
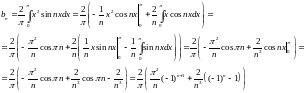
Подставим найденные коэффициенты Фурье в формулу:
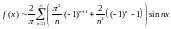 .
.
В
точке
—
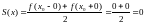 ,
на концах отрезка —
,
на концах отрезка —
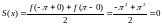 .
.
Задачи для самостоятельного решения
Данные функции разложить в ряд Фурье:
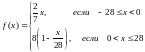
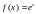 в интервале
в интервале
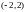
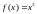 в интервале
в интервале

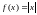 в интервале
в интервале
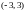
Разложить функцию
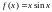 в интервале
в интервале
 в ряд по синусам
в ряд по синусамРазложить функцию в интервале
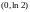 в ряд по косинусам
в ряд по косинусам
Ответы:
1)
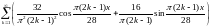 ;
2)
;
2)
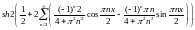 ;
3)
;
3)
 ;
4)
;
4)
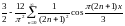 ;
5)
;
5)
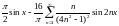 ;
6)
;
6)
 .
.
Список литературы
Фихтенгольц, Г. М. Курс дифференциального и интегрального исчисления : в 3 т. Т. 1 / Г. М. Фихтенгольц. — СПб. : Лань, 2009.
Берман, Г. Н. Сборник задач по курсу математического анализа / Г. Н. Берман. — М. : Наука, 2009.
Сборник задач по математике для втузов : в 4 ч. Ч. 2 / под ред. А. В. Ефимова, А. С. Поспелова. — М. : Физматлит, 2009.
Кузнецов, Л.А. Сборник заданий по высшей математике. Типовые расчеты: Учебное пособие. 9-е изд., стер. — СПб.: Издательство «Лань», 2007.
Стандарт организации СГАУ 02068410-004-2007: Общие требования к учебным текстовым документам. (http://www.ssau.ru/resources/standards)