Задача 5

Куля, що летить із швидкістю v_о, пробиває декілька однакових дошок, які розташовані на деякій відстані одна від одної.

В якій дошці застряне куля , що після проходження першої дошки швидкість кулі зменшилась на 20% ?

Розв’язання:

За теоремою про кінетичну енергію після пробивання першої дошки

Е_к1 - Е_к0 = А_с, або

Оскільки 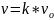- швидкість кулі після проходження першої дошки. = 1-0,2 = 0,8

Тоді

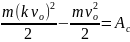
Коли куля застряла в першій дошці, за рахунок кінетичної енергії була виконана робота по подоланню сили опору А = -nА_с

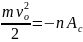
Звідси n = 2,7 3

Отже, куля застряла в третій дошці.

Задача 6

Тіло, кинуте з висоти H=150м вертикально вниз зі швидкістю 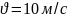, проникло в грунт на глибину h=10 см. Знайти силу опору F грунту, якщо маса тілаm=1кг.

Д ано: Розв’язання

H=150м Зміна повної енергії тіла дорівнює роботі сили опору.

За законом збереження енергії:

h=10 см=0,1м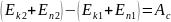

m =1кг

F_c-? ;

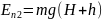
Тоді

Звідси 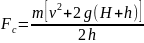Підставимо числові значення

Відповідь: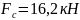

Задача 7

Санчата з’їзджають з гори висотою H=6м. і кутом нахилу α=40^о. Пройшовши шлях S=5 м. по горизонтальній поверхні, вони піднімаються вгору х нахилом β=30 ^о . Визначити на якій висоті h санчата зупиняться, якщо коефіцієнт тертя на всьму шляху дорівнює =0,2.

Д ано: Розв’язання

H=6м Зміна енергії дорівнює роботі сил тертя:

α=40^о Е₁– Е₂=А_тр.

S=5 м Е₂ =Е_п2=mgh;

β=30 ^о Е₁=Е_п1=mgH;

=0,2 Робота сил тертя:

h -? А_тр= А_тр1+ А_тр2+ А_тр3

А_тр1=- =- =- – робота сили тертя при спуску санчат;

А_тр2= – робота сили тертя на горизонтальній ділянці;

А_тр3=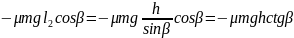 – робота сили тертя при підйомі;

Тоді

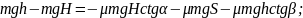
Звідси ; Підставимо числові значення:

Відповідь: h=2,65м.

Задача8

Т

mgF_н2

a_нR

F_н1a_н

іло масою m обертається на нитці у вертикальній площині. На скільки сила натягу нитки в нижній точці більше, ніж у верхній?

Р озв’язання:

З а другим законом Ньютона в нижній точці F_{н1 =} mg +

У верхній точці F_н2 + mg = ; F_н2=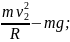

Т оді F_{н1 -} F_{н2 =} mg +

За законом збереження енергії для нижньої і верхньої точки

або

Тоді F_{н1 -} F_{н2 =} 2 mg + = 6 mg

Відповідь: F_{н1 -} F_{н2 =}6 mg

Задача 9

Тіло масою т= 0,5 кг рівномірно оберталось по колу з частотою n₁=5 об/c. В результаті здійснення роботи А = 30 Дж частота збільшилась до n₂=7 об/с. Знайти радіус кола.

Д ано: Розв’язання

т= 0,5 кг Застосуємо один з наслідків закону збереження енергії, в

n₁=5 об/c даному випадку

А = 30 Дж кінетичної, яка дорівнює роботі зовнішніх сил. Тоді

n ₂=7 об/с

R-?

Знайдемо лінійні швидкості тіла , та

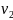
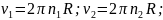
де R- радіус кола. Тоді

Підставимо числові значення, маємо:

Задача 10

Куля масою m₁, яка рухається горизонтально з деякою швидкістю , зіткнулася з нерухомою кулею масою m₂ . Кульки абсолютно пружні, зіткнення пряме, центральне. Яку частку своєї кінетичної енергії перша куля передасть другій?

Розв’язання

Частка енергії, переданої першою кулею другій, виражається співвідношенням

(1)

де T₁ — кінетична енергія першої кулі до зіткнення; u₂ і T₂ - швидкість та кінетична енергія другої кулі після зіткнення.

Як видно з формули (1), для визначення необхідно знайти u₂. Згідно умови задачі, імпульс системи двох куль відносно горизонтального напрямку не зміниться і механічна енергія куль в інші види не переходить. Користуючись цим, знайдемо (2)

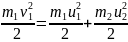(3)

Розв'яжемо разом рівняння (2) та (3):

Підставивши вираз u₂в формулу (1) і скоротивши на , іm₁, отримаємо:

Із знайденого співвідношення видно, шо частка переданої енергії залежить тільки від мас куль, які зіткнулись.

Задача 11

Ящик масою m₁=20 кг зісковзує по ідеально гладкому лотку довжиною l=2м на нерухомий візок з піском і застряє в ньому. Візок з піском масоюm₂₌80 кг може вільно (без тертя) переміщуватися на рейках в горизонтальному напрямку. Визначити швидкість u візка з ящиком, якщо лоток нахилений під кутом 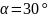до рейок.

Д ано: Розв’язання

m₁=20 кг Візок і ящик можна розглядати як систему двох тіл, які

m₂₌80 кг взаємодіють непружно. l=2м . Але ця

система не замкнена, так як на неї діють зовнішні сили; сили

u-? тяжіння m₁g і m₂g і сили реакції N₂. Тому застосувати закон

Збереження імпульсу до системи ящик - візок неможливо. Але

так як проеції даних сил на напрямок осі X, яка співпадає з напрямком рейок, дорівнюють нулю, то проекцію імпульсу системи на цей напрямок можна вважати постійною, тобто (1)

д е р_1х і р_2х - проекції імпульсу ящика і візка з піском в момент падіння на візок; р_1х і р_2х ті ж величини після падіння ящика.

Розглядаючи тіла системи як матеріальні точки, виразимо в рівнянні (1) імпульси тіл через маси та швидкості враховуючи, що р_2х=0 (візок до взаємодії з ящиком знаходився в стані спокою), а також, що після взаємодії обидва тіла системи рухаються з однаковою швидкістю u:

або , де модуль швидкості ящика

перед падінням на візок; проекція цієї швидкості на вісь X.

Звідси :

Модуль швидкості , визначимо застосувавши закону збережені енергії:

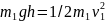
де , звідси Підставивши вираз в (2), отримаємо

Після обчислень знайдемо (м/с)

Задача 12

Ракера встановлена на поверхні Землі для запуску у вертикальному напрямку. Яку мінімальну швидкість , необхідно надати ракеті при запуску, щоб вона віддалилася від поверхні на відстань рівну радіусу Землі ( )? Всіма силами, крім сили гравітаційної взаємодії ракети і Землі знехтувати.

Розв'язання.З боку Землі на ракету діє сила тяжіння , яка є потенціальною силою. При непрацюючому двигуні під дією потенціальної сили механічна енергія ракети змінюватись не буде.

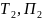Звідси , де і - кінетична та потенціальна енергії ракети після вимкнення двигуна в початковому (біля поверхні Землі) та кінцевому (на відстані рівній радіусу Землі) станах.

Згідно визначення кінетичної енергії

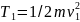
Потенціальна енергія ракети в початковому стані:

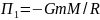
При віддаленні ракети від поверхні Землі її потенціальна енергія зростає , а кінетична - зменшується. В кінцевому стані кінетична енергія буде дорівнювати нулю ,а потенціальна - набуде максимальногозначення:

Підставляючи вирази в (1), отримаємо:

Звідки

Потенціальнаенергіягравітаційноївзаємодіїтіл, нескінченновіддалениходневідодного, приймаєтьсярівноюнулю.

Оскільки ( -прискореннявільногопадіннябіляповерхніЗемлі), запишемоцюформулуувигляді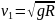 , щоспівпадаєзвиразомдляпершоїкосмічноїшвидкості. Виконаємо розрахунки: (км/с)

Індивідуальні завдання для самостійної роботи студентів.

1. Молот масою m =1,5 т б’є по розжареній болванці, яка лежить на ковадлі і деформує її. Маса ковадла разом з болванкою М = 20 т. Визначити коефіцієнт корисної дії удру молота, вважаючи удар непружним. Роботу, виконану під час деформації болванки, вважати корисною.( ета = 93%)

2. З гармати масою 5 т вилітає снаряд масою 100 кг. Кінетична енергія снаряда при вильоті дорівнює 7,5*10⁶ Дж. Яку кінетичну енергію матиме гармата в результаті віддачі ? (Е_к = 150 кДж)

3. Кулька масою 0,3 кг вдарилася в нерухо­му кулю масою 500 г, яка набуває швидкості 4 м/с. Визначити швидкість першої кульки після удару, якщо перед зіштовхуванням вона мала швидкість 10 м/с, напрямлену під кутом 30° до горизонту. Після взаємодії швидкості кульок горизонтальні. Удар вважати абсолютно пружним. (2 м/с).

4. Куля, яка летить з швидкістю 40 м/с під кутом до горизонту 60°, вдарилася об кулю, яка летить горизонтально зі швидкістю 10 м/с. Ви­значити швидкість куль після удару, якщо маса першої кулі 2 кг, а другої — 8 кг. Після не-пружного удару кулі рухаються горизонтально. (12 м/с)

5. Візок масою ЗО кг, який рухається гори­зонтально зі швидкістю 2 м/с, наздоганяє хлоп­чик і заскакує на нього, після чого швидкість віз­ка стає 5 м/с. Визначити горизонтальну складову швидкості хлопчика під час стрибка. Маса хлоп­чика 55 кг. (6,63 м/с).

6.Метеорит, який летів під кутом до гори­зонту 30°, розвалився на два уламки масами 15 і 45 кг. Визначити швидкість руху метеориту, якщо менший уламок рухається із швидкістю 350 м/с під кутом 45° до горизонту, а біль­ший — вертикально вгору. Опором повітря знехтувати. (133 м/с)

7. Снаряд летить із горизонтальною швидкі-стю 600 м/с і розривається на-два уламки. Один із уламків більшої маси летить по горизонталі, а другий масою, удвічі меншою за масу першого, рухається після вибуху під кутом 30° до горизон­ту. Визначити швидкість другого уламка. (800 м/с).

8. Візок масою 26 кг рухається горизонта­льно зі швидкістю 4 м/с назустріч хлопчику. Ко­ли візок проїжджає повз нього, хлопчик заскакує на візок, після чого швидкість візка стає 1,5 м/с. Визначити горизонтальну складову швидкості хлопчика під час стрибка. Маса хлопчика 60 кг,(0,42м/с)

9. Під кутом до вертикалі 30° із швидкістю 150 м/с летить камінь масою 200 кг і потрапляє в нерухому платформу з піском масою 1 т. Визна­чити швидкість платформи. Тертям коліс знехту­вати. (12,5 м/с)

10. Камінь масою 50 кг потрапляє у плат­форму з піском, яка рухається йому назустріч го­ризонтально зі швидкістю 15 м/с. Визначити ма­су платформи, якщо перед потраплянням камінь мав швидкість 20 м/с, напрямлену під кутом 30° до горизонту. Швидкість платформи з каменем становить 1,6 м/с. Тертям коліс знехтувати. (70,6 кг)

11. Снаряд летить із горизонтальною швид­кістю 900 м/с і розривається на два уламки. Ула­мок більшої маси летить під кутом до горизонту 30°, а другий масою, утричі меншою, рухається після вибуху під кутом 30° до вертикалі зі швид­кістю 250 м/с. Визначити швидкість більшого уламка. (1332 м/с).

12. Людина переходить з краю платформи, що обертається, на відстань, яка дорівнює поло­вині ії радіуса. Як при цьому зміниться її кутова швидкість? Платформа має форму диска. Маса людини 80 кг, маса платформи 200 кг. (Збільшу­ється у 1,5 раза)

13. Людинапереходить ізвідстані, яка до­рівнює половині радіуса платформи, на її край. Як при цьому зміниться кутова швидкість обер­тання платформи? Платформа має форму диска. Маса людини 60кг, маса платформи 120 кг. (Зменшується у 0,63 раза)

14. Диск, момент інерції якого дорівнює 63,6 кг-м² , обертається з кутовою швидкістю 31,4рад/с. Визначити кутову швидкість диска, якщо перемістити тіло масою 1 0 кг з його краю в центр. Радіус диска дорівнює 15 м. (1 142 рад/с)

15. Стрижень довжиною 1 м і масою 7 кг може вільно обертатися навколо горизонтальної осі, яка проходить через його верхній кінець.

У другій кінець стрижня влучає куля масою 5 г, яка летіла зі швидкістю 500 м/с, перпендикуляр­но до осі стрижня і застряла в ньому. Визначити кутову швидкість стрижня після влучання в ньо­го кулі. (0,36 рад/с)

16. На краю горизбнтальної платформи, яка має форму диска радіусом 2 м, стоїть людина. Маса платформи 200 кг, маса людини 80 кг. Плат­форма може обертатися навколо вертикальної осі, яка проходить через її центр. Визначити, з якою кутовою швидкістю буде обертатися плат­форма, якщо людина піде вздовж її краю зі шви­дкістю 2 м/с відносно платформи. (0,44 рад/с)

17. З гори висотою 19,6 м у горизонтальному напрямі кинули камінь зі швидкістю 36 км/год. Ви­значити кінетичну і потенціальну енергії каменя че­рез 1,25 с польоту після початку руху. Маса каменя 100 г. Опором повітря знехтувати. (12,5 Дж; 11,7 Дж)

18. Визначити роботу, яку потрібно викона­ти, щоб збільшити швидкість тіла від 2 до 4 м/с на шляху 12 м, якщо на всьому шляху діє стала сила тертя 2 Н. Маса тіла 1 кг. (26 Дж)

19. Тіло масою 2 кг, яке рухається із швид­кістю 10 м/с, зштовхується з нерухомим тілом.. Вважаючи удар центральним і непружним, ви­значити кількість теплоти, яка виділяється під час удару/Маса другого тіла 3 кг. (98 Дж)

20. Похилою площиною вгору котиться без ковзання обруч масою 1 кг, початкова швидкість якого 8 м/с напрямлена паралельно похилій пло­щині. Під час руху діє сила тертя З Н. Через 6 м обруч зупиняється. Визначити кут нахилу пло­щини. (51,5°)

21. Мідна куля радіусом 10 см обертається з частотою 2 об/с навколо своєї осі, яка прохо­дить через її центр. Яку роботу потрібно викона­ти, щоб збільшити частоту обертання вдвічі? Гу­стина міді — 8900 кг/м³. (35,5 Дж) .

22. Похилою площиною вгору котиться без ковзання куля масою 5 кг, початкова швидкість якої 9 м/с. Під час руху діє сила тертя 25 Н. Через З м куля зупиняється. Визначити кут нахилу пло­щини.. (28,2⁰)

23. Камінь кинуто горизонтально з почат­ковою швидкістю 10 м/с. Визначити кінетичну енергію каменя через три секунди після початку руху. Маса каменя 2 кг. (964,4 Дж) *

24. Визначити роботу сили, якщо на шляху 20 м швидкість тіла змінилася від 2 м/с до 10 м/с. На всьому шляху діє стала сила тертя. Коефіці­єнт тертя 0,1, маса тіла 50 кг. (3380 Дж)

25. Ядро атома розпадається на два уламки масами 1,6-10~²⁵ кг і 2,5-10""²⁵ кг. Визначити кіне­тичну енергію другого уламка, якщо кінетична енергія першого уламка 5-10-¹¹ Дж. (3,2-10-¹¹ Дж).

26. Визначити кількість теплоти, яка виді­ляється під час удару кулі об стінку, якщо її маса дорівнює 1 кг. Швидкість кулі до удару дорівнює 10 см/с, а після — 8 см/с. (2,52-10 Дж).

27. Куля масою 10г, яка летить горизонтально зі швидкістю 600 м/с, влучила в балістичний маятник масою 5 кг і застряла в ньому. На яку висоту після удару піднімається маятник? (70 см).

28. Куля масою 10 г, яка летить зі швидкіс­тю 600 м/с, влучила в балістичний маятник дов­жиною 1 м і масою 5 кг і застряла в ньому. На який кут після удару відхилився маятник? (22°).

29. Куля радіусом 5 м обертається навколо власної осі. Визначити роботу, яку потрібно ви­конати, щоб збільшити частоту обертання кулі від 2 об/с до 4 об/с. Маса кулі 1 кг. (2366,3 Дж)

30. Однорідний циліндр масою 5 кг котиться без ковзання горизонтально з початковою швид­кістю 14 м/с. Який шлях пройде циліндр до зу­пинки, якщо сила тертя дорівнює 50 Н? (14,7 м)

31. Однорідна куля масою 2 кг кІггитьсІГЄез ковзання горизонтально. Який шлях пройде куля, якщо її швидкість зменшилася від 14 м/с до 2 м/с. Сила тертя, що діє на всьому шляху, дорівнює 20Н? (13,4м)

32. Угору похилою площиною котиться без ковзання обруч із початковою швидкістю 3,14 м/с, яка паралельна похилій площині. Визначити шлях, який пройде обруч похилою площиною, якщо кут нахилу площини 30°. Тертям знехтувати. (2 м)

33. Угору похилою площиною котиться без ковзання куля із початковою швидкістю 4,5 м/с. Визначити висоту, на яку вона може піднятися вздовж похилої площини. (1,5 м)

34.Угору похилою площиною котиться без ковзання обруч із початкової швидкістю 5 м/с. Визначити кут нахилу похилої площини, якщо шлях, який пройде обруч похилою площиною, дорівнює 15м. (10°)

35. Тіло масою" 2 кг рухається зі швидкістю 3 м/с і наздоганяє інше тіло масою 3 кг, що рухається зі швидкістю 1 м/с. Знайти швидкості тіл після зіткнення, якщо: 1) удар був непружним; 2) удар був пружним. Тіла рухаються по одній прямій, удар був центральним.

(1) vi= У₂= 1,8 м/с; 2) уі = 0,6 м/с, У₂= 2,6 м/с)

36. На скільки переміститься відносно берега човен довжиною 3,5 м і масою 200 кг, якщо людина масою 80 кг, що стоїть на кормі, перейде на ніс човна? Вважати човен розташованим перпендикулярно до берега.

S= 1 м)

37. Снаряд, горизонтальна швидкість якого 600 м/с, розривається на два осколки. Маса одного осколка в два рази більша, ніж другого. Осколок більшої маси падає вертикально, а меншої рухається під кутом 30° до горизонту. Визначити швидкість меншого осколка.

(v₂ = 2078 м/с)

38. Снаряд летить з горизонтальною швидкістю 600 м/с та розривається на два осколки. Один з осколків більшої маси летить по горизонталі зі швидкістю 800 м/с, а інший масою в два рази меншою ніж у першого рухається після розриву під кутом 30° до горизонту. Яка швидкість другого осколка?

(v₂ = 400м/с)

39. Човен довжиною / = Зм та масою М— 120 кг стоїть на спо-кійній воді. На носу та кормі знаходяться два рибалки масамиm₁ = 60 кг та m₂ = 90 кг. На скільки зміститься човен відносно води, якщо рибалки пройдуть по човну та поміняються місцями?

(l = 0,33м)

40. Куля масою m₁= 10кг стикається з кулею масою m₂ = 4 кг. Швидкість першої кулі vi= 4 м/с, другої - v₂ = 12 м/с. Знайти загальну швидкість и куль після удару в двох випадках: коли мала куля доганяє більшу кулю, яка рухається в тому ж напрямку, та коли кулі рухаються назустріч одна одній. Удар вважати прямим, центральним, непружним.

( и₁= 6,28м/с; и₂ = -0,572м/с)

41. Куля, яка рухається горизонтально, зіштовхується з нерухомою кулею та передає їй 64% своєї кінетичної енергії. Кулі абсолютно пружні, удар прямий, центральний. У скільки разів маса другої кулі більша за масу першої?

( m_1/ m₂ = 4)

42. Куля масою т₁ = 6 кг рухається зі швидкістю vi= 2 м/с і зіштовхується з кулею масою т₂ = 4 кг, яка рухається їй назустріч зі швидкістю v₂ = 5 м/с. Знайти швидкості куль після прямого центрального удару. Кулі вважати абсолютно пружними.

(и₁ = - 3,6м/с ;(и₂= 3,4м/с)

43. Дерев'яна куля масою М = 10 кг підвішена на нитці довжиною l= 2м. Вкулю попадає кулька масою т = 5 г, що летить горизонтально та застрягає в ній. Визначити швидкість кульки, якщо нитка з кулею відхилилася від вертикалі на кут а = 3 . Розміром кулі знехтувати. Удар кульки вважати центральним.

(v= 463,6 м/с)

44. Диск масою т =1 кг і діаметром D= 60 см обертається навколо осі, яка проходить через його центр перпендикулярно площині диска, з частотою п = 20 об/с. Яку роботу необхідно виконати, щоб зупинити диск. (А=355Дж)

45. Кінетична енергія вала, який обертається зі сталою швидкістю, що відповідає частоті п= 5 об/с, дорівнює 60 Дж. Знайти момент імпульсу цього вала. (L= 3.8кг-м²/с)