
- •Комплект контрольно-измерительных материалов по дисциплине
- •40.02.01 «Право и организация социального обеспечения»
- •Общие положения
- •Результаты освоения предмета
- •Формы контроля предмета
- •Контроль результатов освоения предмета
- •3. Критерии оценки:
- •4. Критерии оценки:
- •Практическая работа №1:
- •Практическая работа №2: «Производные высших порядков»
- •Практическая работа №3: «Дифференциал функции»
- •Практическая работа №4: «Исследование функции с помощью производной»
- •Практическая работа №5: «Основные методы интегрирования»
- •Практическая работа №6: «Интегрирование рациональных функций»
- •Практическая работа №7: «Интегрирование тригонометрических функций»
- •Практическая работа №8: «Интегрирование иррациональныx выражений»
- •Тестовые задания к зачету:
- •Паспорт фонда оценочных средств
4. Критерии оценки:
- оценка «отлично» выставляется обучающемуся, если задание выполнено на 100%;
- оценка «хорошо» выставляется обучающемуся, если выполнено не менее 70% задания;
- оценка «удовлетворительно» выставляется обучающемуся, если выполнено не менее 50% задания;
- оценка «неудовлетворительно» выставляется обучающемуся, если выполнено менее 50% задания.
Приложение 1.
Практическая работа №1:
«Производная суммы, разности, произведения и частного элементарных функций. Производная сложной функции»
Задание 1: Найти производную следующих функций:
Номер варианта |
Задания |
1. |
|
2. |
|
3. |
|
|
|
4. |
|
5. |
|
6. |
|
Задание 2: Найти производную сложной функции:
Номер варианта |
Задания |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
Задание 3: Найти производную суммы, разности, произведения или частного тригонометрических функций:
Номер варианта |
Задания |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
Приложение 2.
Практическая работа №2: «Производные высших порядков»
Задание 1: Найти производную второго порядка:
Номер варианта |
Задания |
1. |
1)
|
2. |
1)
|
3. |
1)
|
4. |
1)
|
5. |
1)
|
6. |
1)
|
Задание 2: Найти производную третьего порядка:
Номер варианта |
Задания |
1. |
1)
|
2. |
1)
4)
|
3. |
1)
|
4. |
1)
|
5. |
1)
|
6. |
1)
|
Задание 3: Проверьте, что функция у является решением данного дифференциального уравнения:
Номер варианта |
Задания |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
Задание 4: Точка движется по закону S(t). Найдите величины скорости и ускорения в заданный момент времени.
Номер варианта |
Задания |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
, |
6. |
, |
Приложение 3.

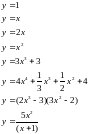
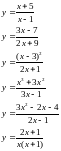

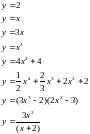
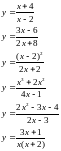
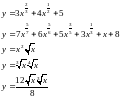
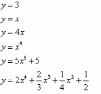
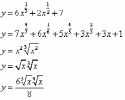
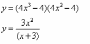
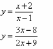
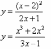
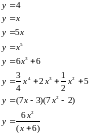

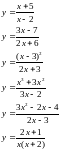


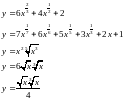

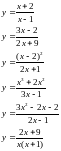

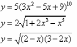
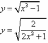
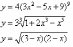
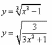

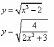
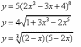
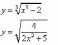
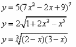


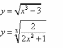

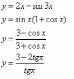
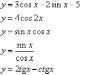
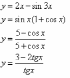
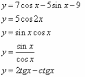
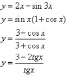

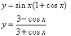
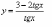




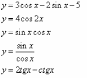

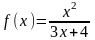 ;
2)
;
2)
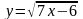 ;
3)
;
3)
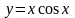 ;
4)
;
4)
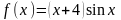 .
. ;
2)
;
2)
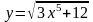 ;
3)
;
3)
 ;
4)
;
4)
 .
. ;
2)
;
2)
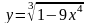 ;
3)
;
3)
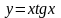 ;
4)
;
4)
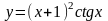
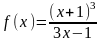 ;
2)
;
2)
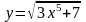 ;
3)
;
3)
 ;
4)
;
4)
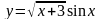
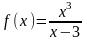 ;
2)
;
2)
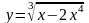 ;
3)
;
3)
 ;
4)
;
4)

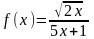 ;
2)
;
2)
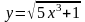 ;
3)
;
3)
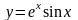 ;
4)
;
4)

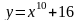 ;
2)
;
2)
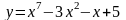 ;
3)
;
3)
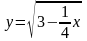 ;
4)
;
4)
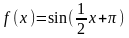 .
.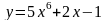 ;
2)
;
2)
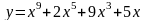 ;
3)
;
3)
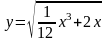 ;
;
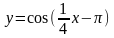 .
.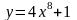 ;
2)
;
2)
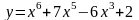 ;
3)
;
3)
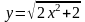 ;
4)
;
4)
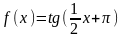
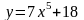 ;
2)
;
2)
 ;
3)
;
3)
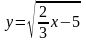 ;
4)
;
4)
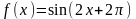
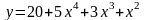 ;
2)
;
2)
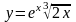 ;
3)
;
3)
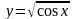 ;
4)
;
4)
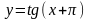
 ;
2)
;
2)
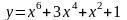 ;
3)
;
3)
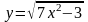 ;
4)
;
4)
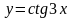
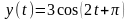 ,
,
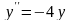
 ,
,

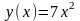 ,
,

 ,
,
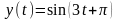 ,
,
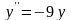
 ,
,
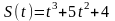 ,
,
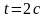
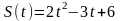 ,
,

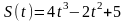 ,
,
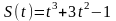 ,
,