1.2 Методика моделирования линейных дифференциальных уравнений на аналоговых решающих элементах. Расчеты начальных условий

Для составления схемы аналогового моделирования используется уравнение в виде, в котором коэффициент при старшей производной р^п выходного сигнала у равен единице.

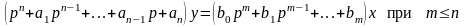(1.10)

При невыполнении этого условия необходимо разделить обе части дифференциального уравнения на коэффициент при р^пу.

Если моделируемый объект описывается системой дифференциальных уравнений вида

(1.11)

то обозначив ту переменную, которую считают выходным сигналом системы, и подлежащую расчету, как у, например уу₁, переписываем (1.11) в матричной форме

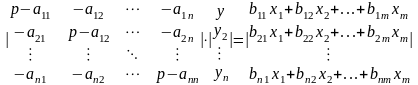(1.12)

Затем находим решение у системы (1.12) как функцию от входных переменных х₁, х₂,… х_m. Если рассчитывается реакция только на один входной сигнал, например х₁, то остальные сигналы х₂, х₃, … х_m принимаем равными нулю, а сигнал х₁ обозначаем как х. В результате получаем одно дифференциальное уравнение стандартного вида (1.10).

Подготовка дифференциального уравнения (1.10) к решению на аналоговой модели состоит из нескольких этапов (для простоты изложения примем условие m=n):

1). Из (1.10) выражаем выходной сигнал у следующим образом:

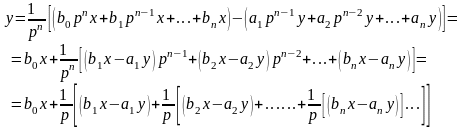(1.13)

В полученном выражении содержатся деление членов на символ р в первой степени. Такие члены могут быть промоделированы на многовходовом интеграторе.

2). По выражению (1.13) составляем структурную схему (рис.1.3) решающего устройства, используя обозначения, приведенные на рис.1.1,б и рис.1.2,б.

Рисунок1.3 - Структурная схема решающего устройства аналоговой модели

3). Составляем принципиальную электрическую схему решающего устройства, используя принципиальные схемы сумматора (рис.1.1) и многовходового интегратора (рис.1.3), и рассчитываем величины сопротивлений резисторов и емкостей конденсаторов.

Числовой пример.

Пусть некоторый объект описывается дифференциальным уравнением

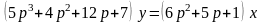
при начальных условиях

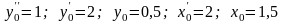(1.14)

Составление схемы аналогового моделирования заключается в последовательном выполнении следующих действий:

1). Делим обе части дифференциального уравнения на 5 (коэффициент при старшей производной от у):

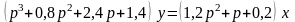(1.15)

Из (1.15) следует

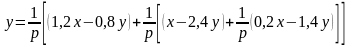(1.16)

2). По выражению (1.16) составляем структурную схему решающего устройства (рис.1.4).

Рисунок 1.4 - Структурная схема решающего устройства

В структурной схеме обозначены два промежуточных сигнала у₁ и у₂, которые использованы ниже для расчета начальных условий для интеграторов.

3). На основании начальных условий (1.15) определяем начальные условия для выходных сигналов всех интеграторов схемы решающего устройства. Расчеты ведем, продвигаясь по схеме (рис.1.4) справа - налево.

Начальное условие для выходного сигнала у ОУ3 равно начальному значению у₀, указанному в системе (1.15):

у₀=0,5 V (1.17)

Для вычисления начального значения сигнала у₂ опишем уравнением работу ОУ3 по рис.1.4. В интегральной форме уравнение работы ОУ3 имеет вид

,

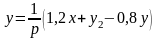а в дифференциальной форме –

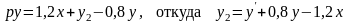(1.18)

Начальное значение сигнала у₂ согласно (1.18) и (1.15) равно

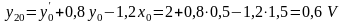
Для вычисления начального значения сигнала у₁ опишем уравнением работу ОУ2 по рис.1.4. В интегральной форме уравнение работы ОУ2 имеет вид

,

а в дифференциальной форме –

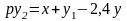
откуда с учетом (1.15) и (1.18) получим

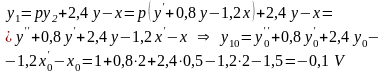(1.19)

Задача решена.