Евклидов изоморфизм
Как и в случае абстрактных линейных пространств, введем понятие изоморфизма, что позволит переносить многие результаты из пространств направленных отрезков, т.е. обычной геометрии, в евклидовы пространства.
Определение 8.18. Два евклидовых
пространства
и
называются евклидово изомофными, если
они изоморфны как вещественные
пространства, т.е. существует изоморфизм
,
и при этом для любых
выполнено
.
Разумеется, есть нужда в критерии евклидовой изоморфности.
Теорема 8.7 (критерий евклидовой изоморфности).
Два евклидовых пространства евклидово изоморфны тогда и только тогда, когда имеют одинаковую размерность.
Доказательство. Необходимость очевидна, ибо тогда данные пространства изоморфны как вещественные пространства (см. т. 5.9).
Достаточность. Пусть
.
Выберем ортонормированные базисы в
указанных пространствах:
в
и
в
.
Тогда для произвольных векторов
имеем с отображением
по правилу
в силу свойства ортонормированных
базисов:
.
Само же отображение
,
очевидно, биективное и линейное. Например,
.
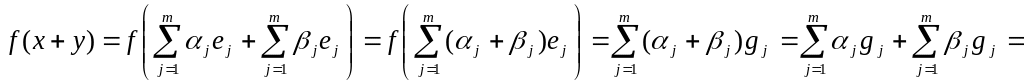
На основании понятия изоморфизма можно утверждать что результаты, справедливые в
трехмерном наглядном пространстве будут справедливыми в любом трехмерном подпространстве евклидова пространства, а значит в любом евклидовом пространстве.
Определитель Грама
В этом параграфе введем новый объект, обладающий многими интересными свойствами, некоторые из которых будут рассмотрены.
Определение 8.19. Пусть
– евклидово пространство и
.
Определителем Грама системы
называется определитель вида
.
Во-первых докажем теорему, которую можно рассматривать как одно из свойств определителя Грама.
Теорема 8.8 (критерий линейной зависимости системы векторов).
Система векторов евклидова пространства линейно зависима тогда и только тогда, когда ее определитель Грама равен нулю.
Доказательство. Необходимость.
Пусть система
– линейно зависима. По первому критерию
линейной зависимости (см. т. 5.3) существует
ненулевой набор вещественных чисел
такой, что
.
Будем считать, для определенности, что
.
Тогда умножая мысленно первые
строку определителя соответственно на
числа
(их первые сомножители) и прибавляя к
последней строке, умноженной на
,
получим, по известному свойству
определителей, величину
.
Но этот определитель будет содержать
в последней строке элементы
для
,
т.е. будет содержать нулевую строку.
Значит,
и тем самым
.
Достаточность. Пусть теперь
.
Следовательно, его строки линейно
зависимы. Это значит, что существует
ненулевой набор
такой, что линейная комбинация строк с
этими числами будет равна нулевой
строке. В частности, в
-ой
позиции этой линейной комбинации будет
присутствовать число
.
Если теперь каждый такой элемент умножить
на
,
,
и просуммировать по
,
от 1 до
,
то получим скалярный квадрат:
.
Если скалярный квадрат равен нулю, то сам вектор равен нулю. Значит,
,
т.е. система линейно зависима. Что и требовалось. Теорема доказана.
Рассмотрим некоторые другие свойства определителя Грама.
1. Пусть система – линейно независима. Тогда
,
где система
получена из системы
процессом ортогонализации Грама-Шмидта.
2.
Если система
линейно независима, то
.
3.
.
Равенство справа достигается тогда и только тогда, когда векторы попарно ортогональны или один из них равен нулю.
Доказательство первого свойства основано на применении формул ортогонализации и применяемых последовательно к первым сомножителям скалярных произведений, а потом ко вторым. Второе свойство является прямым следствием первого и теоремы 8.8. Докажем третье свойство, точнее правое неравенство. Из первого свойства имеем, что
.
В силу того, что система ортогональна, получаем, что
.
Остается показать, что для любого
.
Действительно,
=
.
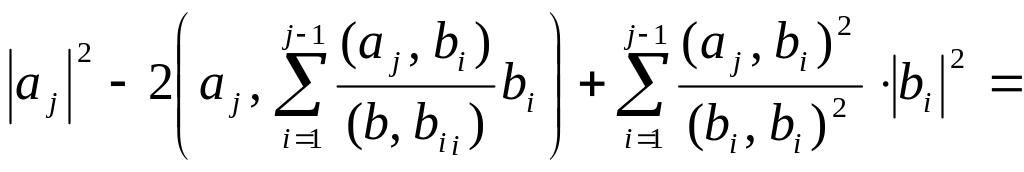
Так как в последнем неравенстве вычитается число неотрицательное, то имеем, что
,
т.е.
,
что и требовалось.