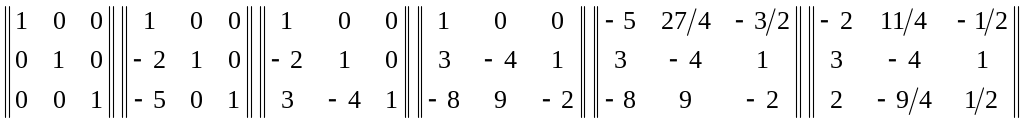Элементарные преобразования матрицы
Определение 4.22. Элементарными преобразованиями (ЭП) матрицы называются
1. Транспозиция двух строк (столбцов) матрицы.
2. Умножение любой строки (столбца) на элемент отличный от нуля.
3. Прибавление к любой строке (столбцу) матрицы любой другой строки (-го столбца) этой матрицы.
Теорема 4.11. Пусть задана матрица . Элементарными преобразованиями строк и столбцов ее можно привести к диагональному виду.
Доказательство. Предположим,
что элемент
![]() .
Тогда умножая первую строку на элементы
.
Тогда умножая первую строку на элементы
![]() и прибавляя соответственно ко второй
и т.д., к
-й
строке получим матрицу вида
и прибавляя соответственно ко второй
и т.д., к
-й
строке получим матрицу вида
 ,
,
А затем, работая подобным образом со столбцами, получаем матрицу
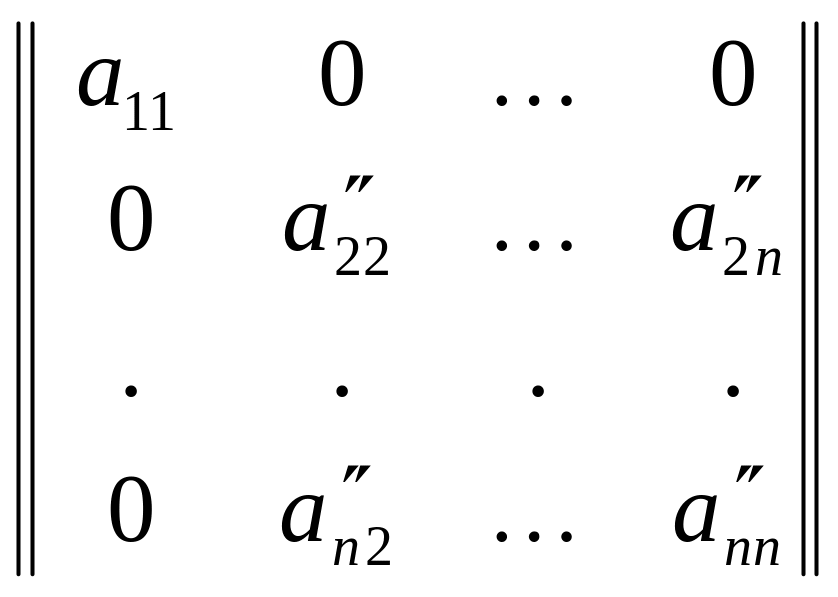 .
.
После этого можно применить индукцию по порядку матрицы.
Если
,
то переставим на первое место строку с
первым ненулевым элементом, а если таких
нет, переставим на первое место столбец
с первым ненулевым элементом. Наконец,
если и таких столбцов нет, то продолжаем
рассуждения с элементом
![]() .
Теорема доказана.
.
Теорема доказана.
Теорема 4.12. Пусть задана матрица . Тогда ее можно привести к диагональному виду элементарными преобразованиями одних лишь строк (столбцов).
Доказательство. Допустим, что будем работать со строками. Тогда снова обратимся к элементу . Если он не равен нулю, то снова, как в предыдущей теореме, получим матрицу
.
Если же
,
то выведем на первое место строку с
ненулевым первым элементом. Такая строка
обязательно существует, ибо в противном
случае матрица оказывается вырожденной.
Надо отметить, что преобразования,
применяемые здесь, могут изменить лишь
знак определителя, и, таким образом,
преобразованная матрица остается
невырожденной. Далее, переходим к работе
с элементом
![]() .
Если он отличен от нуля, то получим нули
во втором столбцу под элементом
,
а если он равен нулю, то перестановками
строк, начиная с третьей, выведем на
второе место строку с нулевым первым
элементом и ненулевым вторым. Такая
строка обязательно найдется среди строк
с номерами от 3 до
,
ибо в противном случае, раскрывая
определитель матрицы по первому столбцу,
получим нуль. Продолжая этот процесс,
получим в итоге верхнюю треугольную
невырожденную матрицу. Наконец, начинаем
производить нули указанным выше способом
над главной диагональю, начиная с
последней строки и последнего столбца.
Теорема доказана.
.
Если он отличен от нуля, то получим нули
во втором столбцу под элементом
,
а если он равен нулю, то перестановками
строк, начиная с третьей, выведем на
второе место строку с нулевым первым
элементом и ненулевым вторым. Такая
строка обязательно найдется среди строк
с номерами от 3 до
,
ибо в противном случае, раскрывая
определитель матрицы по первому столбцу,
получим нуль. Продолжая этот процесс,
получим в итоге верхнюю треугольную
невырожденную матрицу. Наконец, начинаем
производить нули указанным выше способом
над главной диагональю, начиная с
последней строки и последнего столбца.
Теорема доказана.
Следствие. Невырожденную матрицу можно с помощью ЭП привести к единичной.
Определение 4.23. Элементарной матрицей 1-го типа называется квадратная матрица вида
 .
.
Эта матрица получается из единично перестановкой -й и -й строк местами.
Определение 4.24. Элементарной матрицей 2-го типа называется квадратная матрица вида

с
![]() .
.
Определение 4.25. Элементарной матрицей 3-го типа называется квадратная матрица вида
 .
.
Легко видеть, что матрицы всех трех типов невырожденные. Сформулируем следующий результат.
Лемма 4.2. Элементарные преобразования строк матрицы можно заменить умножением соответствующих элементарных матриц на данную матрицу слева, а элементарные преобразования столбцом – умножением на соответствующие элементарные матрицы справа.
Лемма носит очевидный характер, и ее справедливость проверяется непосредственно.
Пусть теперь задана матрица
![]() .
Элементарными преобразованиями строк
приведем ее к единичной. Это можно
описать матричной форме:
.
Элементарными преобразованиями строк
приведем ее к единичной. Это можно
описать матричной форме:
![]() ,
,
где
![]() – элементарные матрицы подходящих
типов. Умножая это равенство на
,
получаем, что
– элементарные матрицы подходящих
типов. Умножая это равенство на
,
получаем, что
![]() .
.
Это наблюдение дает возможность получить еще один метод обращения матриц. Именно, приводя данную невырожденную матрицу к единичной ЭП строк и выполняя те же преобразования над единичной матрицей в итоге получим из единичной обратную к данной.
Пример 4.11. Найдем указанным способом обратную матрицу из примера 4.10.