
- •Задания высокого уровня сложности с развернутым ответом №18
- •Общая постановка задачи с параметром.
- •Основные методы решения задач с параметрами.
- •1. Поиск решения задачи с параметрами.
- •Решение относительно параметра.
- •Симметрия и четность.
- •4. Элементы графического исследования в задачах с параметрами.
- •4.1. Координатная плоскость. Построение параметрического семейства кривых (метод сечений).
- •4.2. Координатно – параметрическая плоскость. Метод областей.
- •5. Функциональный подход к решению уравнений и неравенств.
4.2. Координатно – параметрическая плоскость. Метод областей.
При
графическом исследовании задач с
параметрами наряду с координатной
плоскостью
целесообразно также использовать
координатно – параметрическую плоскость
![]() .
Если возможно построить на координатно
– параметрической плоскости множество
всех точек, координаты которых
и
удовлетворяют условию задачи, то затем
нетрудно поставить в соответствие
каждому значению параметра
этого множества значение соответствующей
координаты
.
Это и будет решением задачи. Следует
также указать те значения параметра,
при которых задача не имеет решения.
Выбор контрольных значений параметра
определяется конкретным видом построенных
множеств.
.
Если возможно построить на координатно
– параметрической плоскости множество
всех точек, координаты которых
и
удовлетворяют условию задачи, то затем
нетрудно поставить в соответствие
каждому значению параметра
этого множества значение соответствующей
координаты
.
Это и будет решением задачи. Следует
также указать те значения параметра,
при которых задача не имеет решения.
Выбор контрольных значений параметра
определяется конкретным видом построенных
множеств.
(ЕГЭ 2011). Найдите все значения , при каждом из которых система
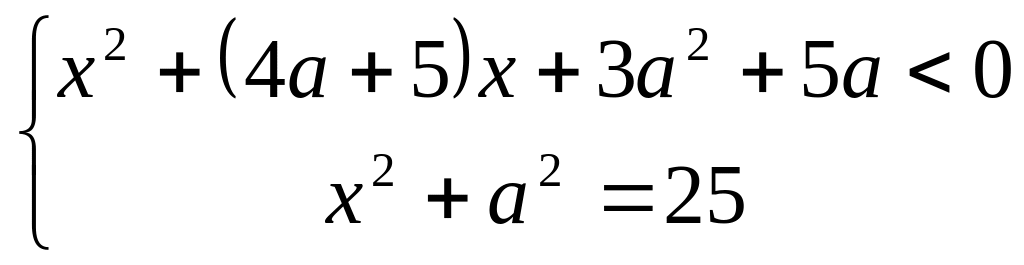 имеет решения.
имеет решения.
Решение
Разложим
левую часть неравенства на множители
![]() .
Это неравенство задаёт пару вертикальных
углов плоскости
.
Это неравенство задаёт пару вертикальных
углов плоскости
![]() .
Уравнение задаёт окружность с центром
.
Уравнение задаёт окружность с центром
![]() радиуса 5.
радиуса 5.

Решения системы – точки дуг окружности, лежащие в указанных вертикальных углах. Абсциссы концов этих дуг находим из систем
![]() и
и
![]()
![]()
![]()
;
.
![]() ;
;
![]() .
.
Ответ:
![]() ;
;
![]() .
.
Найдите все значения параметра , при котором уравнение
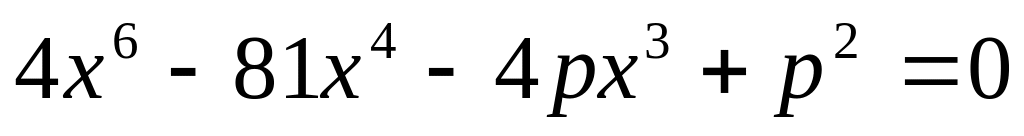 имеет нечетное число различных корней.
имеет нечетное число различных корней.
Решение
Разложим левую часть уравнения на множители:
![]() ;
;
![]() .
.
Таким образом, получили следующую совокупность двух уравнений:
![]() .
.
На
плоскости
![]() построим
графики функций
построим
графики функций
![]() и
и
![]()
![]()
![]()
![]() -
точка максимума
-
точка максимума
-
точка максимума
-
точка максимума
![]() -точка
минимума
-
точка минимума
-точка
минимума
-
точка минимума
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.

Ответ: -27; 0; 27.
Найдите все значения , при каждом из которых общие решения неравенств
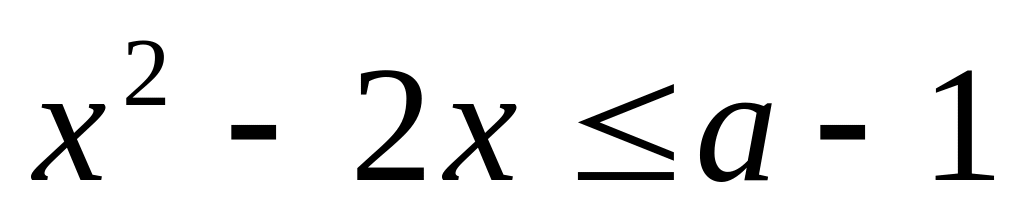 и
и
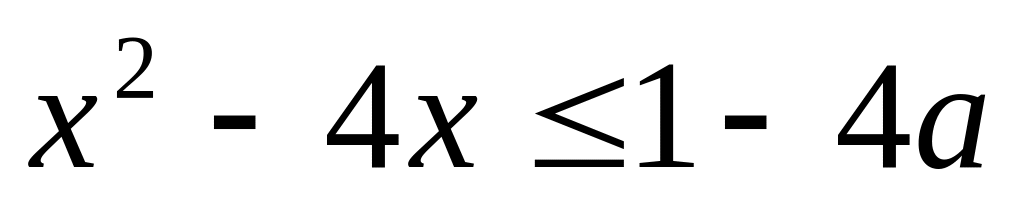 образуют на числовой оси отрезок длины
единица.
образуют на числовой оси отрезок длины
единица.
Решение.
Представим
данные неравенства в виде следующей
системы:
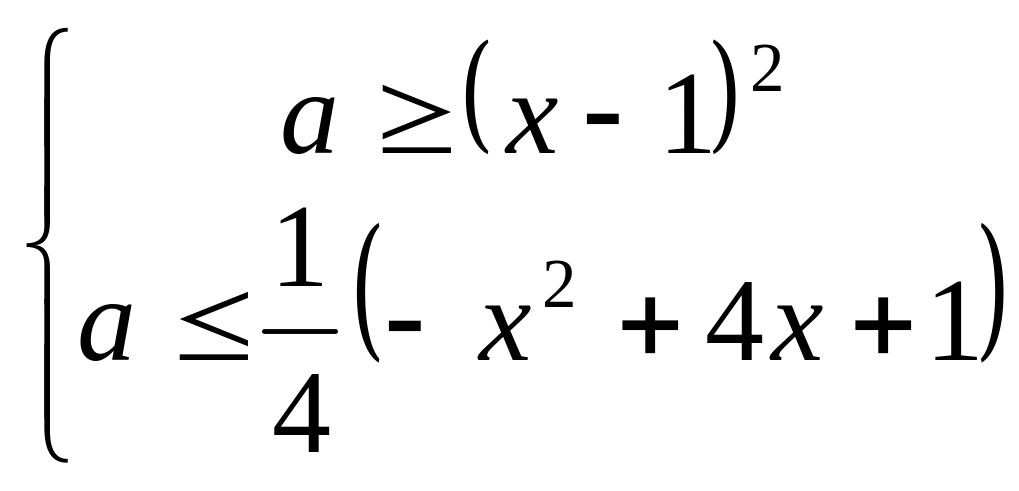 .
.
На
плоскости
![]() решением этой системы являются точки,
лежащие не ниже параболы
решением этой системы являются точки,
лежащие не ниже параболы
![]() и не выше параболы
и не выше параболы
![]() .
.
Найдем точки пересечения этих парабол:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отметим,
что так как
![]() ,
то точка пересечения парабол с координатами
,
то точка пересечения парабол с координатами
![]() лежит правее вершины параболы
,
координаты которой
лежит правее вершины параболы
,
координаты которой
![]() .
.
Решим относительно уравнения
![]() и
и
![]()
![]() ;
;
![]() .
.
Таким образом, следует рассмотреть три системы:
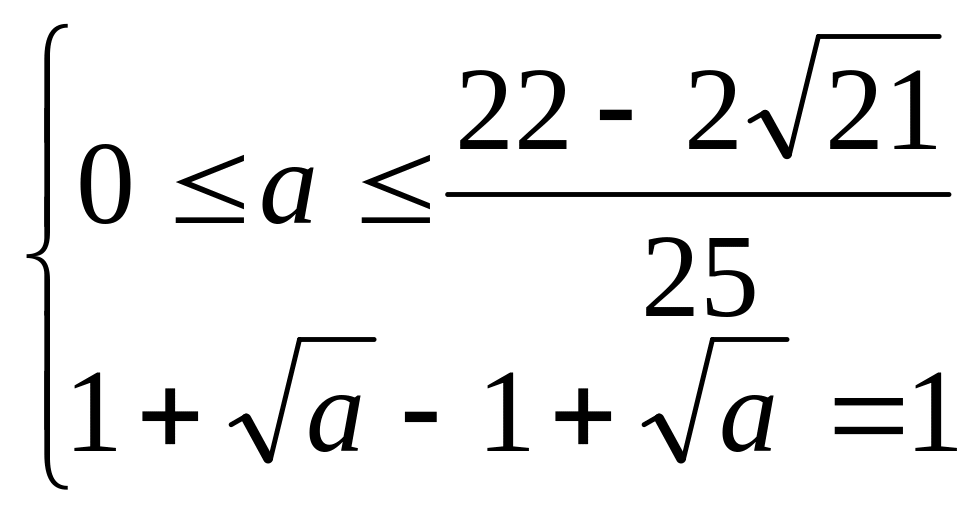 ;
;
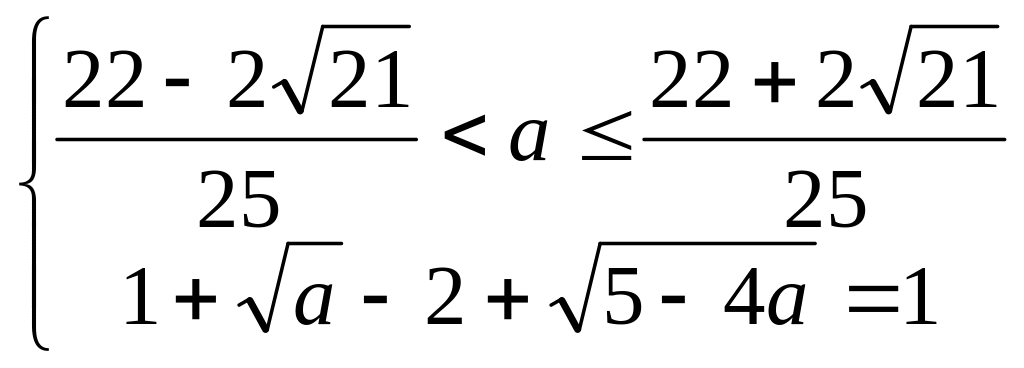 ;
;
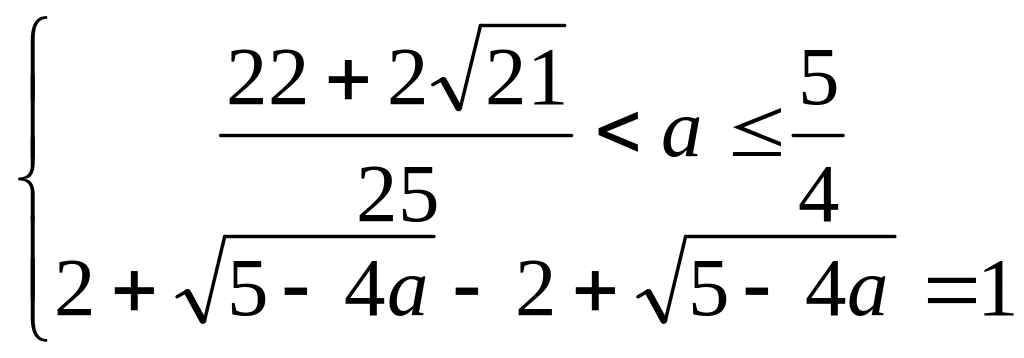
![]()

Решение
системы
:
![]() ;
системы
:
.
;
системы
:
.
Система
несовместна, так как решение второго
уравнения системы
![]()
![]() .
.
Ответ: ; .
5. Функциональный подход к решению уравнений и неравенств.
Для решения уравнений и неравенств, содержащих различные типы элементарных функций, достаточно часто приходится использовать общие методы исследования свойств функций, такие как область определения и множество значений, четность, монотонность, экстремумы и т.д.
Найти все значения , при которых уравнение
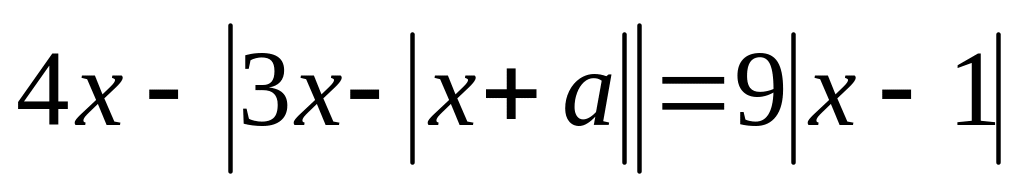 имеет хотя бы один корень.
имеет хотя бы один корень.
Решение.
Рассмотрим уравнение
![]() ,
где
,
где
![]() .
Здесь
.
Здесь
![]() - кусочно-линейная функция, графиком
которой является ломаная линия, имеющая
своими звеньями отрезки прямых и два
луча.
- кусочно-линейная функция, графиком
которой является ломаная линия, имеющая
своими звеньями отрезки прямых и два
луча.
Любое
звено этой ломаной при
![]() - часть некоторой прямой с угловым
коэффициентом
- часть некоторой прямой с угловым
коэффициентом
![]() Для
Для
![]() любое из звеньев имеет угловой коэффициент
любое из звеньев имеет угловой коэффициент
![]() Отсюда следует возрастание
при
и ее убывание при
.
Таким образом,
Отсюда следует возрастание
при
и ее убывание при
.
Таким образом,
![]()
![]() .
.
Условие
существования корня данного уравнения
имеет вид:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Ответ:
.
.
Ответ:
.
Найти все значения параметра , при которых неравенство
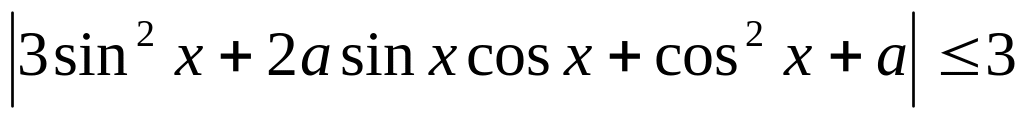 выполняется для любого значения
.
выполняется для любого значения
.
Решение.
Найдем
область изменения функции, стоящей под
знаком модуля.
![]() ,
где
,
где
![]() - дополнительный аргумент.
- дополнительный аргумент.
![]() .
.
Таким образом, получаем следующую систему
![]()
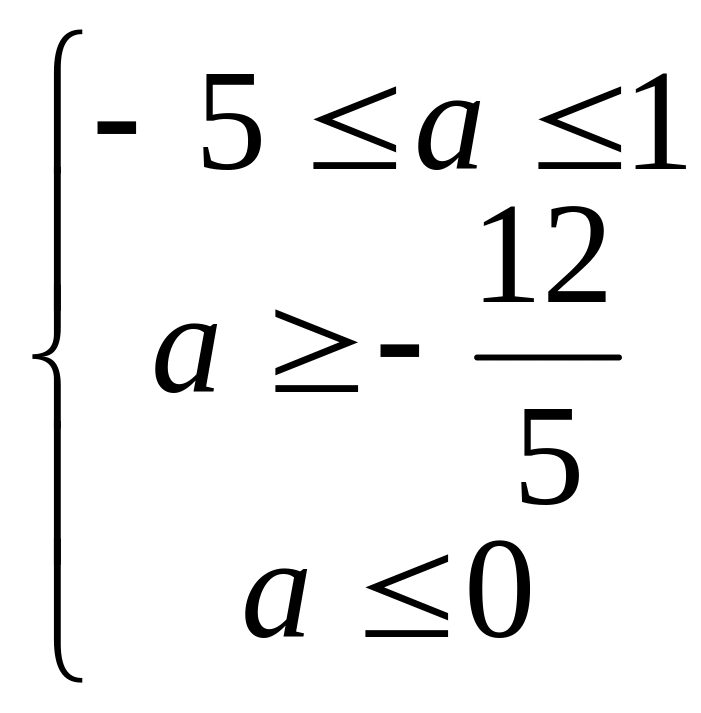
![]() .
Ответ:
.
Ответ:
![]() .
.
(ЕГЭ 2012). Найдите все значения параметра , при каждом из которых неравенство
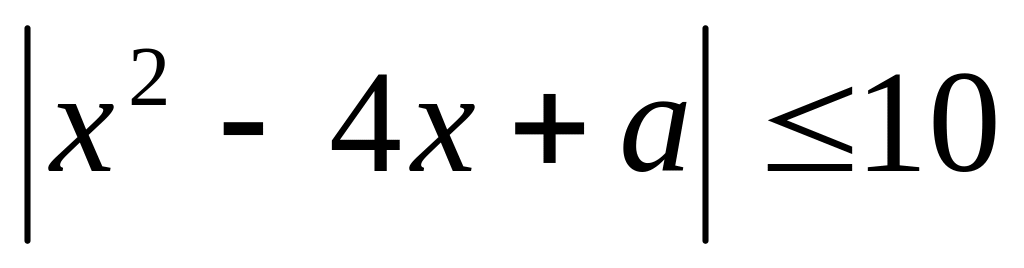 выполняется для всех
выполняется для всех
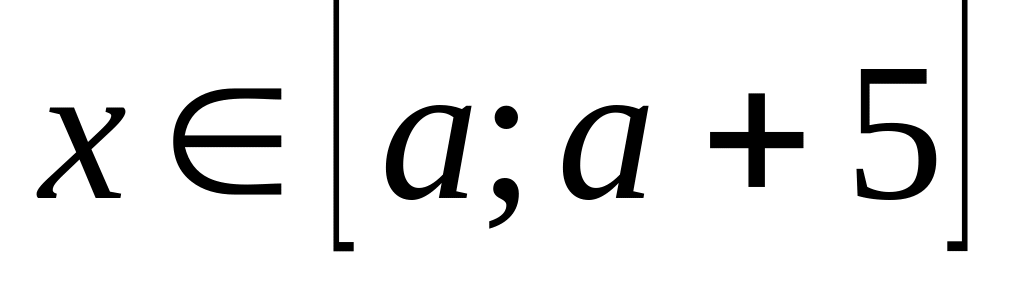 .
.
Решение.
Рассмотрим функцию
![]() =
=![]() .
.
Эта
функция возрастает на промежутке
![]() и убывает на промежутке
и убывает на промежутке
![]() .
.
![]() ;
;
![]() .
.
Отрезок
![]() не должен лежать на участке монотонности,
иначе
не должен лежать на участке монотонности,
иначе
![]() .
.
Следовательно,
![]() ;
;
![]() .
.
Наибольшее
значение
![]() достигается либо при
достигается либо при
![]() ,
либо при
,
либо при
![]() .
.
Наименьшее
значение
достигается при
![]() .
Итак, имеем систему:
.
Итак, имеем систему:
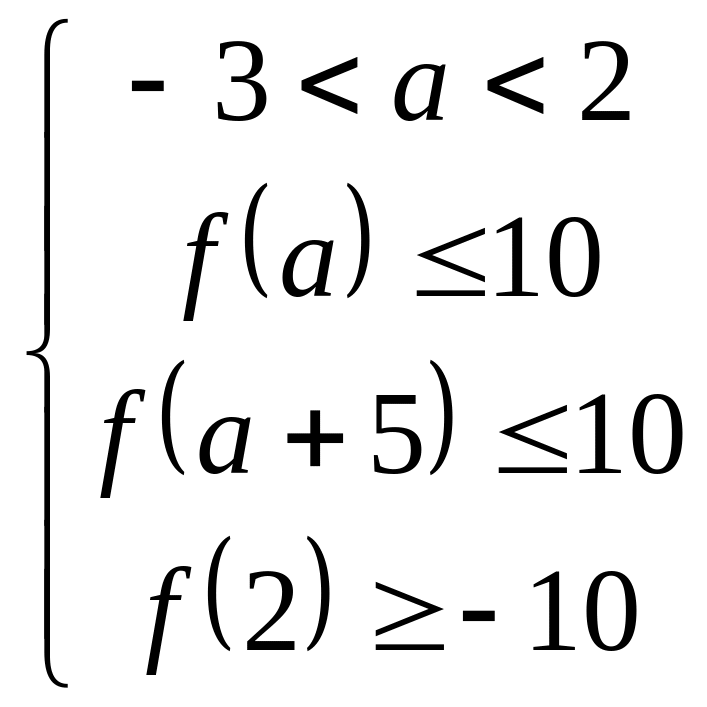
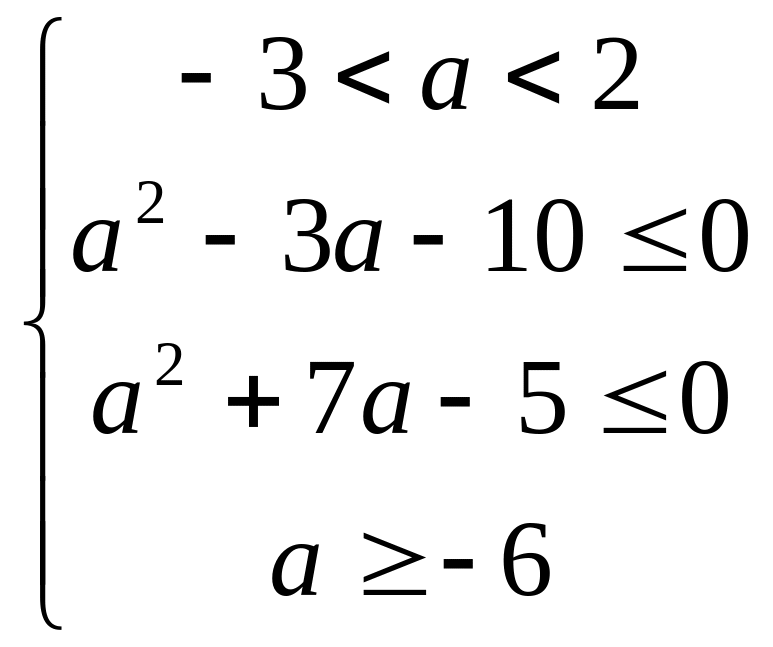
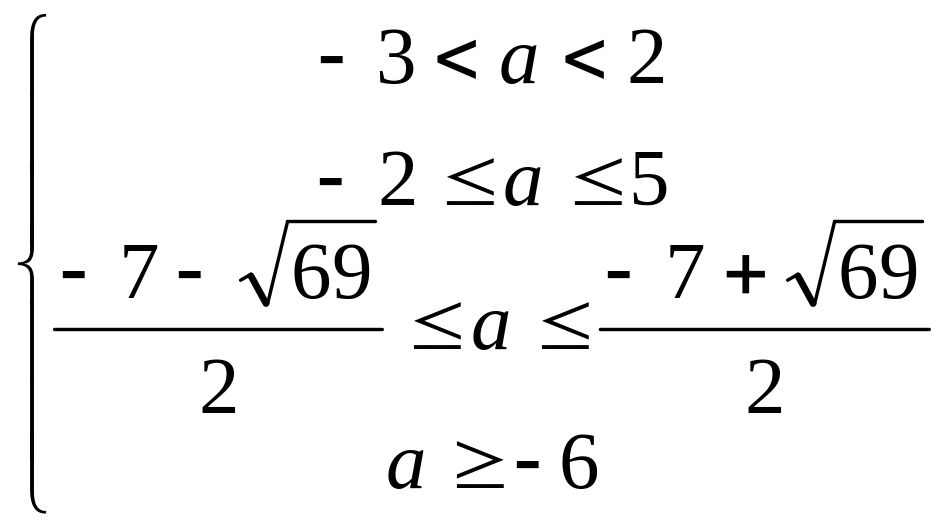
Ответ:
![]() .
.
(ЕГЭ 2013). Найдите все значения параметра , при каждом из которых уравнение
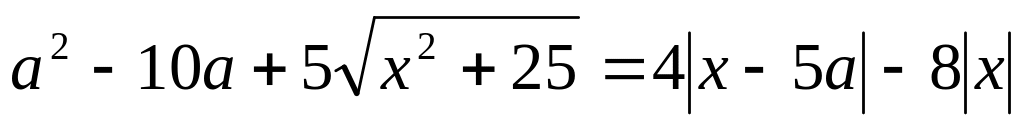 имеет хотя бы один корень.
имеет хотя бы один корень.
Решение.
Рассмотрим две функции:
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Функция является кусочно-линейной.
При
![]() угловой коэффициент либо 4 , либо 12.,
угловой коэффициент либо 4 , либо 12.,
при
![]() угловой коэффициент либо -4 , либо -12.
угловой коэффициент либо -4 , либо -12.
Значит,
![]() возрастает
при
и убывает при
,
поэтому
возрастает
при
и убывает при
,
поэтому
![]() .
.
Исходное
уравнение имеет хотя бы один корень
тогда и только тогда, когда
![]() .
.
![]()
![]() или
или
![]()
![]()
![]()
Ответ:
-5;
![]() ; .
; .
(ЕГЭ 2012). Найдите все значения параметра , при каждом из которых уравнение
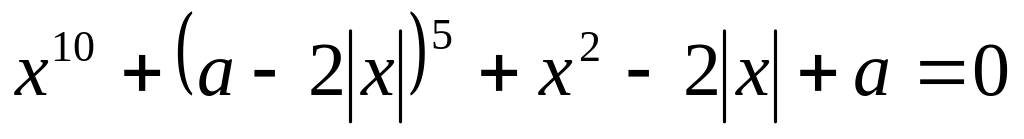 имеет более трех различных решений.
имеет более трех различных решений.
Решение.
Перепишем уравнение в виде
![]() или
или
![]() ,
где
,
где
![]() .
.
![]() ,
следовательно,
,
следовательно,
![]() - монотонно возрастающая функция.
- монотонно возрастающая функция.
![]() .
.
![]() ;
;
![]()
![]() -
два решения при
-
два решения при
![]() ;
;
![]() -
два решения при
,
отличных от решений первого уравнения.
-
два решения при
,
отличных от решений первого уравнения.
Ответ: .
.
Найдите все значения параметра , при каждом из которых уравнение
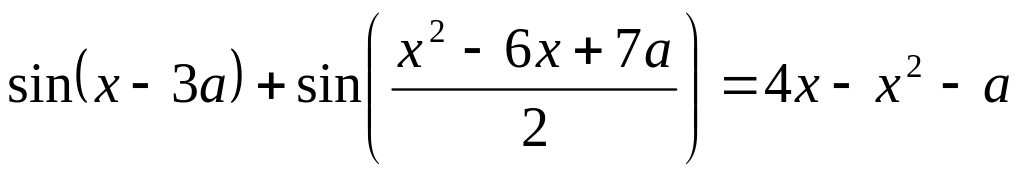 не имеет действительных решений.
не имеет действительных решений.
Решение.
Обозначим
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
В результате указанной замены исходное уравнение примет следующий вид:
![]() .
.
Введем
функцию
![]() и запишем уравнение в виде
и запишем уравнение в виде![]() или с учетом нечетности
:
или с учетом нечетности
:
![]()
Так
как
![]() ,
то
-монотонно
возрастающая функции, то
,
то
-монотонно
возрастающая функции, то
![]() .
.
Отсюда
имеем
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найдите наибольшее целое значение , при котором уравнение
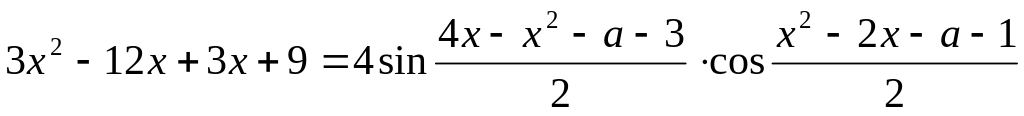
имеет ровно два различных решения.
Решение
Преобразуем
правую часть уравнения по формуле
![]() .
.
Получим
![]() .
.
Левую часть уравнения преобразуем следующим образом:
![]() .
.
Обозначим
![]() ;
;
![]() ,
тогда уравнение примет вид:
,
тогда уравнение примет вид:
![]() или
или
![]()
Введем
функцию
![]() .
.
Так
как
![]() ,
то
-монотонно
возрастающая функция.
,
то
-монотонно
возрастающая функция.
Следовательно,
![]()
![]() .
.
Отсюда
имеем
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ: .
Найти все значения параметра , при каждом из которых уравнение
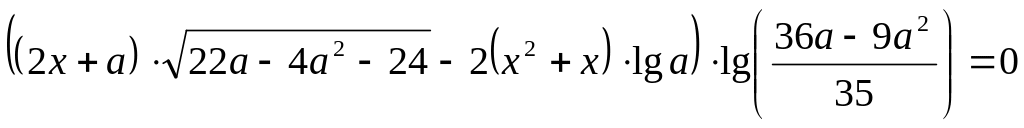 имеет по крайней мере два корня, один
из которых неотрицателен, а другой не
превосходит
имеет по крайней мере два корня, один
из которых неотрицателен, а другой не
превосходит
-1.
Решение. Найдем ОДЗ:
![]()
![]()

![]() .
.
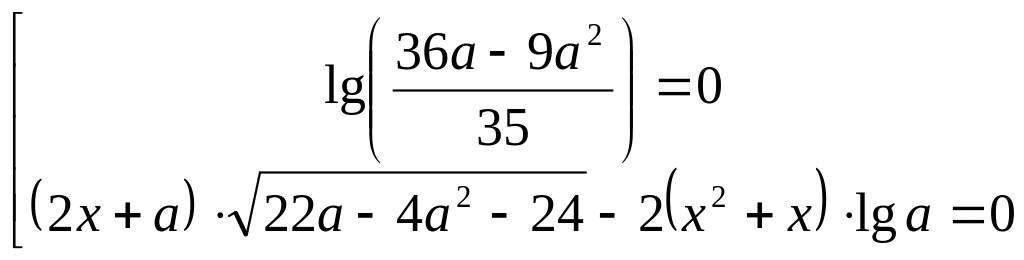
![]()
![]()
![]()
![]()
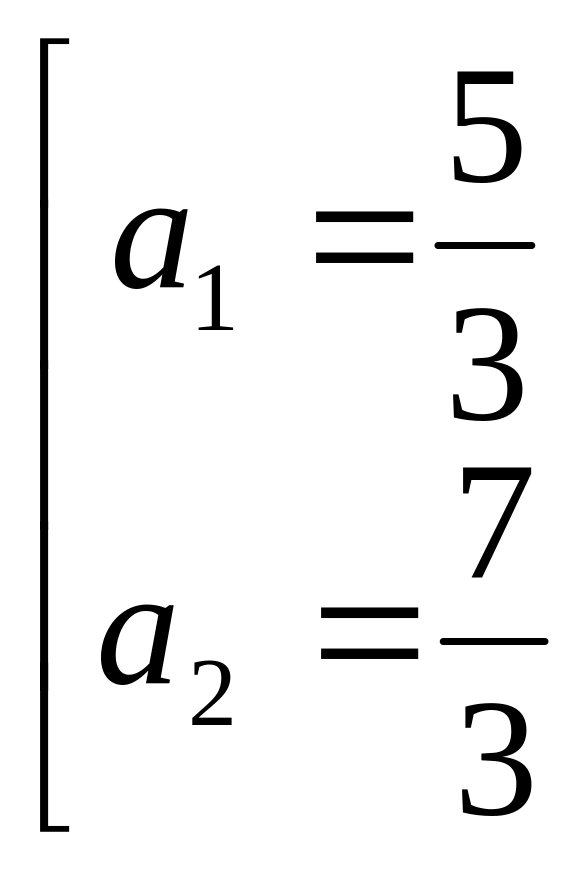
![]()
![]()
![]()
![]()
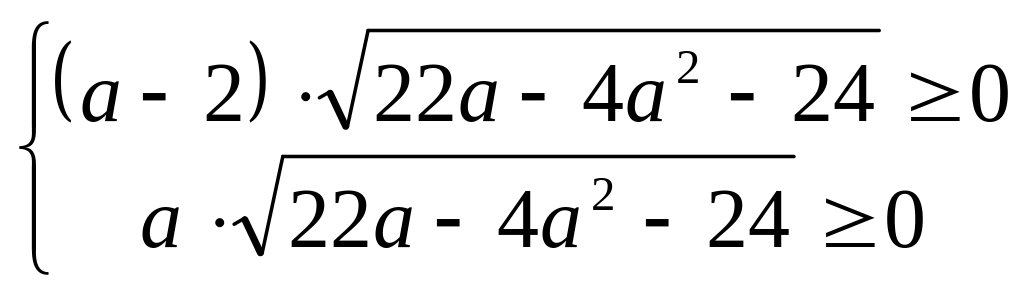
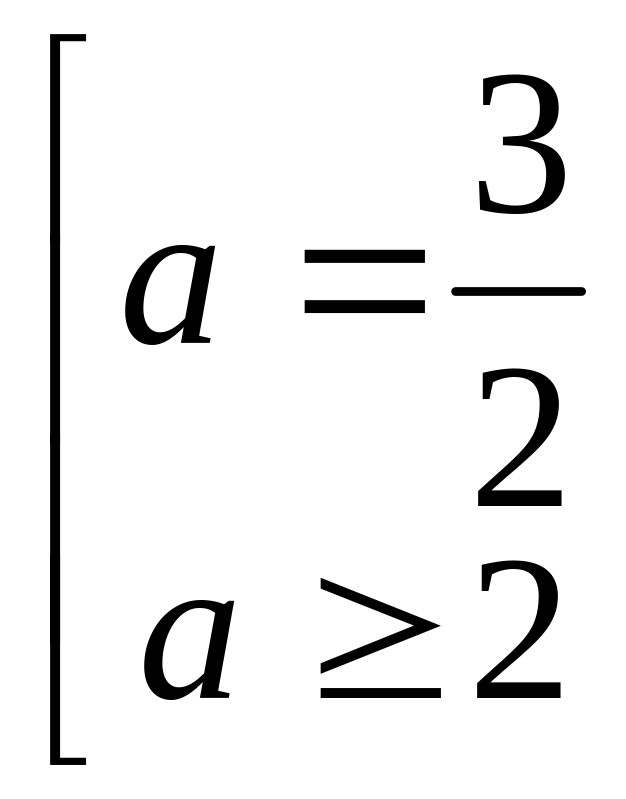
![]() .
.
Ответ:
![]() ;
;
![]() ;
;
![]() .
.
При каких значениях параметра неравенство
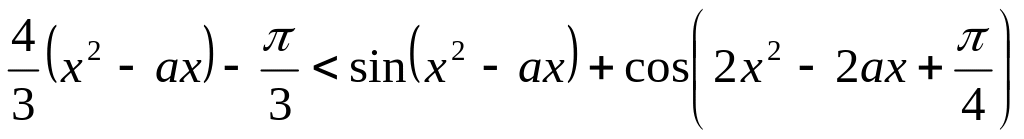 справедливо для всех значений
из отрезка
справедливо для всех значений
из отрезка
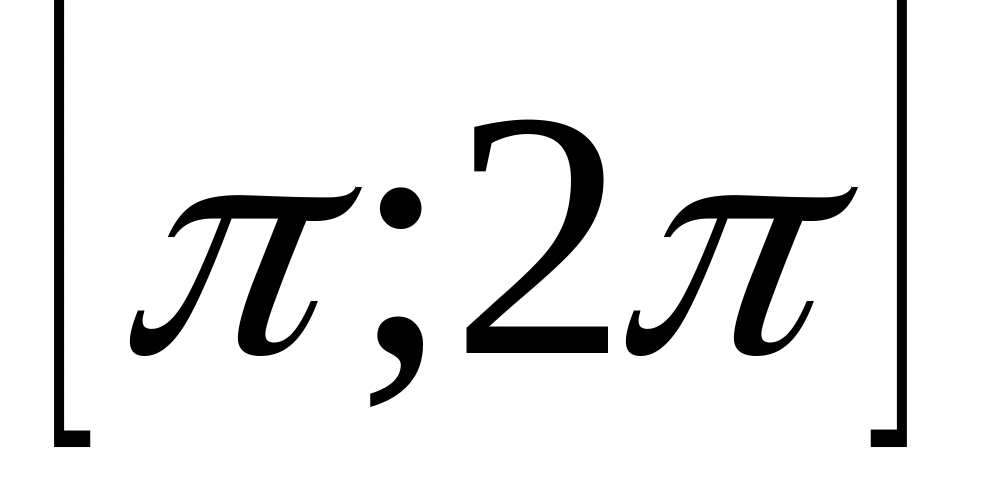 ?
?
Решение.
Обозначим
![]() ,
тогда неравенство будет иметь вид
,
тогда неравенство будет иметь вид
![]()
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]() -
монотонно возрастающая функция;
-
монотонно возрастающая функция;
![]() ;
;
![]() ;
;
![]() .
.
![]()
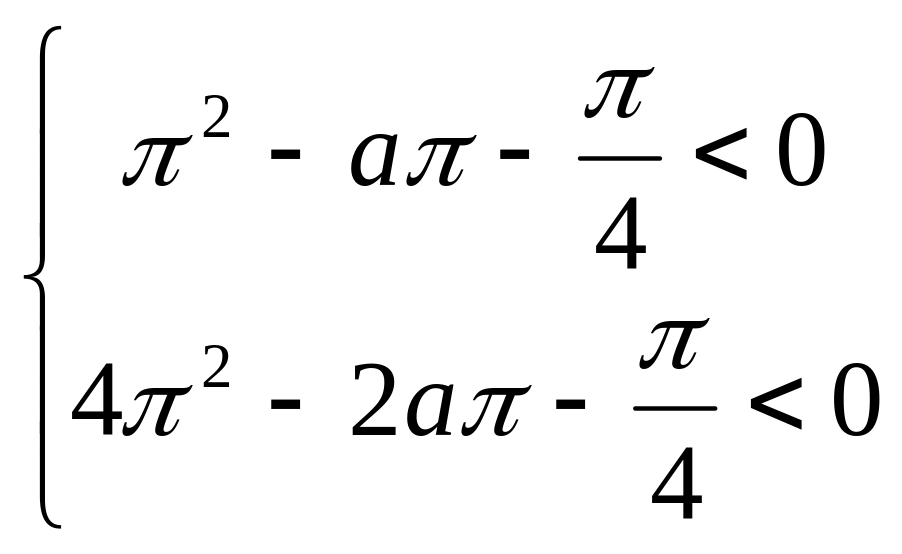

Ответ;
![]() .
.
(ЕГЭ 2014). Найдите все значения параметра , при которых для любого действительного выполнено неравенство
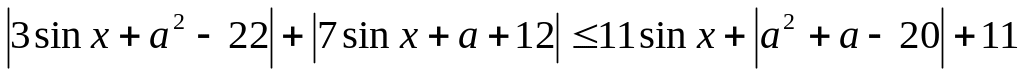
Решение.
Пусть
![]() ,
тогда неравенство запишется в виде
,
тогда неравенство запишется в виде
![]() .
Поскольку
.
Поскольку
![]() ,
нам требуется найти все значения
,
при которых неравенство выполнено при
,
нам требуется найти все значения
,
при которых неравенство выполнено при
![]() .
.
Рассмотрим
функции
![]()
![]() и
и
![]() .
Функция
- кусочно-линейная. Угловой коэффициент
ее звеньев не превосходит 10. Функция
.
Функция
- кусочно-линейная. Угловой коэффициент
ее звеньев не превосходит 10. Функция
![]() - линейная функция с угловым коэффициентом
11. Значит, функция
- линейная функция с угловым коэффициентом
11. Значит, функция
![]() возрастающая. Свое наименьшее значение
на промежутке
возрастающая. Свое наименьшее значение
на промежутке
![]() она принимает при
она принимает при
![]() .
Таким образом, если неравенство
.
Таким образом, если неравенство
![]() выполнено при
,
то оно выполняется и при
выполнено при
,
то оно выполняется и при
![]() .
.
При
неравенство принимает вид
![]() ;
;
![]() .
.
![]() при
при
![]() .
.
![]()
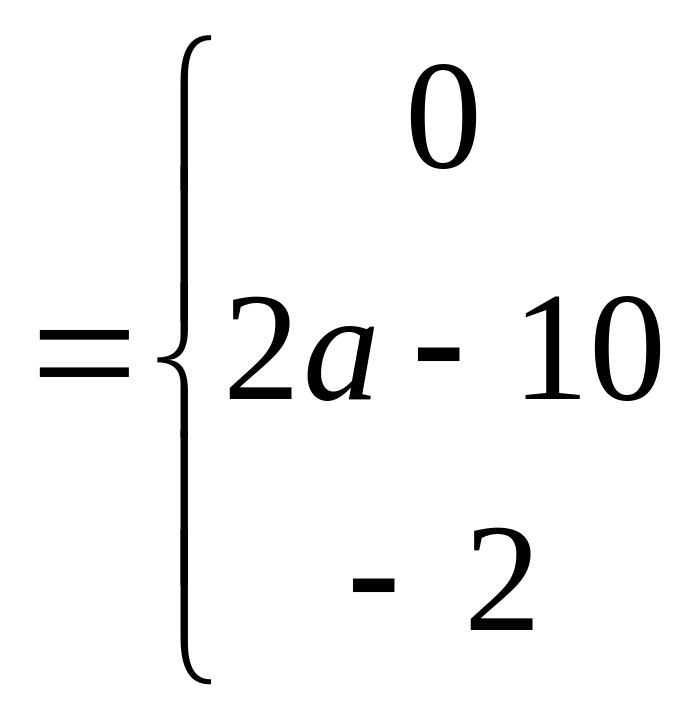
![]()
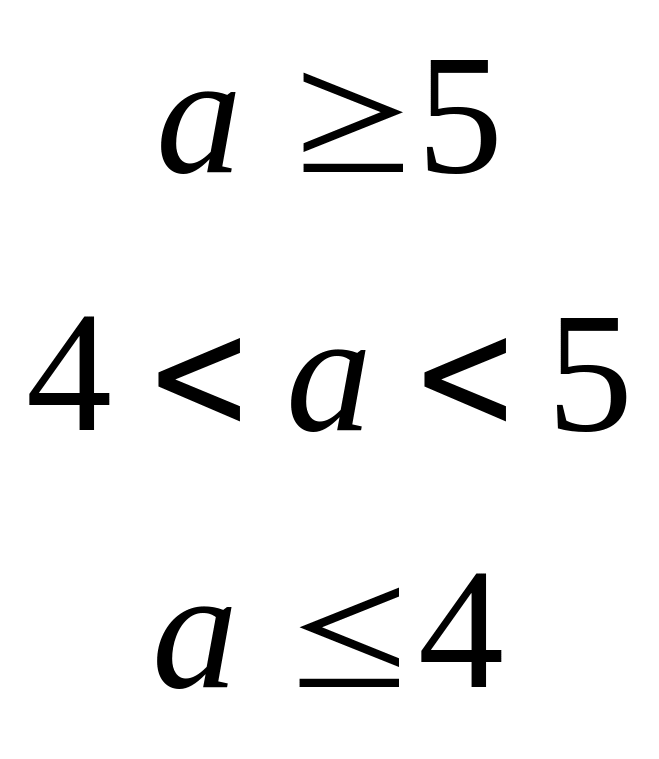 .
.
Таким
образом,
при
;
![]() .
.
Ответ:
![]() ;
;
![]() .
.
(ЕГЭ 2014). Найдите все значения параметра , при которых уравнение
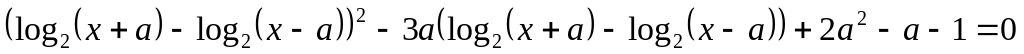 имеет ровно два решения.
имеет ровно два решения.
Решение.
Пусть
![]() ,
тогда уравнение имеет вид
,
тогда уравнение имеет вид
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
При
![]() решений
нет.
решений
нет.
ОДЗ:
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
![]() -
монотонно убывающая функция.
-
монотонно убывающая функция.
При
![]()
![]() ;
;
![]() .
.
Таким
образом, при
выражение
![]() принимает по одному разу все значения
из промежутка
принимает по одному разу все значения
из промежутка
![]() .
.
При
![]()
![]() ;
.
;
.
При
выражение
принимает по одному разу все значения
из промежутка
![]() .
При
.
При
![]() имеем одно решение
имеем одно решение
![]() .
.
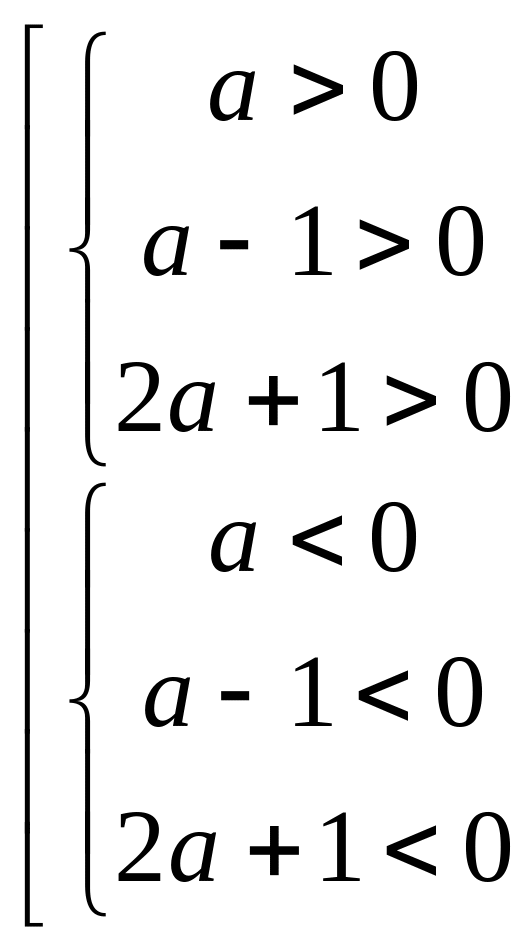 ;
;
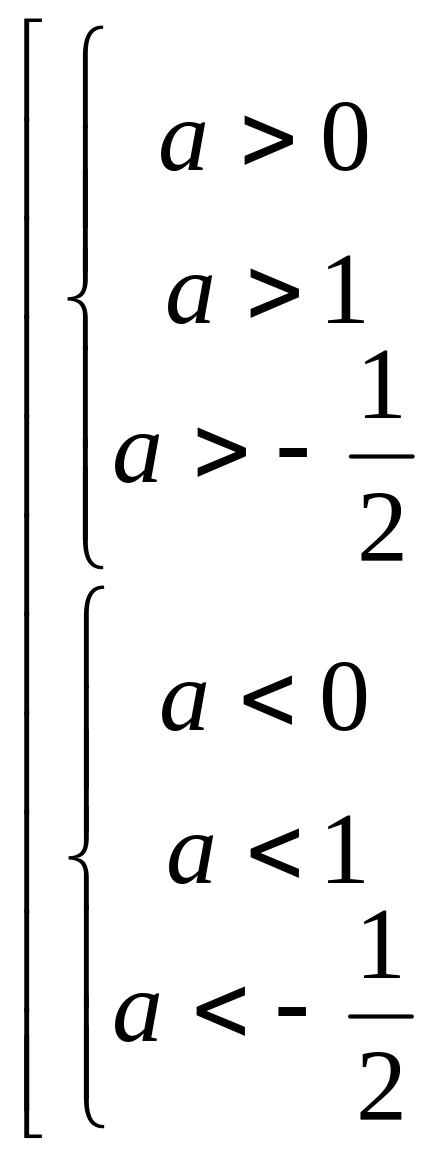 ;
;
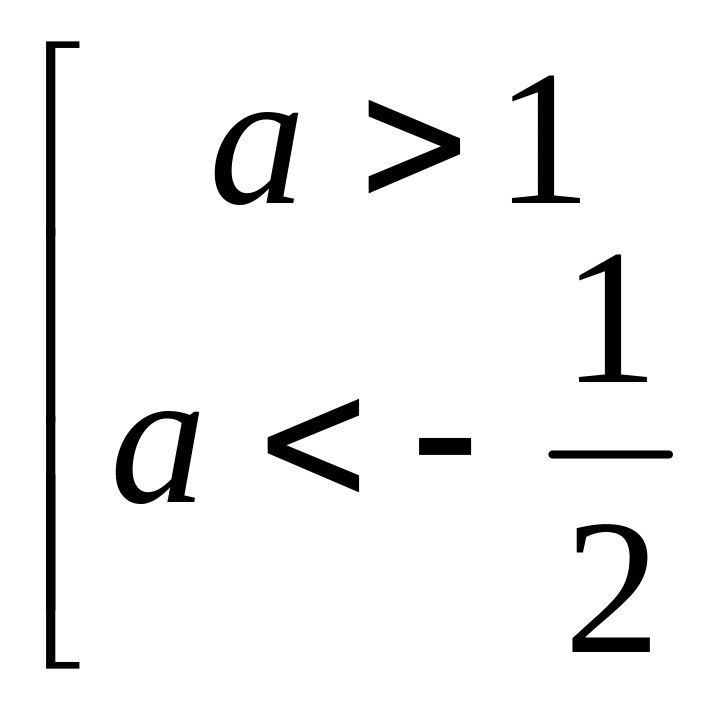 .
.
Ответ:
![]() ;
;
![]() ;
.
;
.
-
Содержание критерия
Баллы
Обоснованно получен правильный ответ
4
С помощью верного рассуждения получено множество значений , отличающееся от искомого только включением точек
 и/или
и/или
3
С помощью верного рассуждения получен один из промежутков множества : или ; возможно, с включением граничных точек и/или исключением точки
2
Верно найдена хотя бы одна из граничных точек множества значений или ; ИЛИ получено хотя бы одно из уравнений
1
Решение не соответствует ни одному из критериев, перечисленных выше.
0
Максимальный балл
4
Найдите все значения , при каждом из которых уравнение
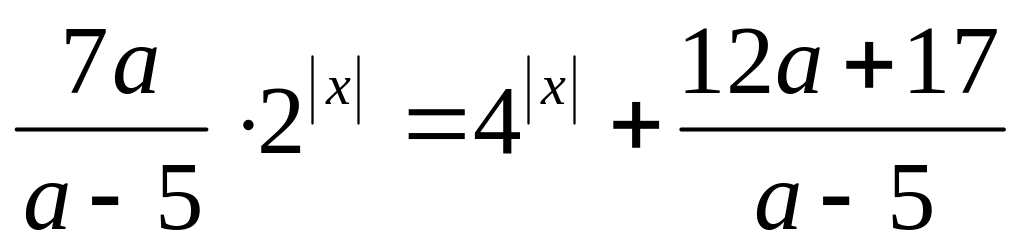 имеет ровно два различных корня.
имеет ровно два различных корня.
Решение.
Пусть
![]() ,
,
![]() .
.
Если
![]() ,
тогда
,
тогда
![]() ,
,
![]() и
и
![]() .
.
Если
![]() ,
тогда
,
тогда
![]() ;
;
![]() .
.
Обозначим
![]() .
.
Исходное
уравнение имеет ровно два корня тогда
и только тогда, когда уравнение
![]() имеет
единственный корень, больший 1, или два
корня, один из которых больше 1, а другой
меньше 1.
имеет
единственный корень, больший 1, или два
корня, один из которых больше 1, а другой
меньше 1.
Уравнение
имеет единственный корень, если его
дискриминант равен нулю:
![]() ;
;
![]() ;
;
![]() или
или
![]() .
.
При
уравнение
![]() имеет единственный корень
.
В этом случае исходное уравнение имеет
единственный корень
.
имеет единственный корень
.
В этом случае исходное уравнение имеет
единственный корень
.
При
уравнение
![]() имеет единственный корень
имеет единственный корень
![]() .
В этом случае исходное уравнение имеет
два корня.
.
В этом случае исходное уравнение имеет
два корня.
Графиком
функции
![]() является парабола, ветви которой
направлены вверх. Для того, чтобы
уравнение
имело два корня, один из которых больше
1, а другой меньше 1, необходимо и
достаточно, чтобы выполнялось неравенство
является парабола, ветви которой
направлены вверх. Для того, чтобы
уравнение
имело два корня, один из которых больше
1, а другой меньше 1, необходимо и
достаточно, чтобы выполнялось неравенство
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ: -170; (-2; 5).
Найти все значения параметра , при каждом из которых множество значений функции
 содержит отрезок
содержит отрезок
 .
.
Решение.
Перепишем заданную функцию так:
![]() .
.
Для
того, чтобы множество значений функции
содержало отрезок
,
необходимо, чтобы уравнения
![]() (1) и
(1) и
![]() (2) имели корни, т.е. нашлись такие
значения переменной
,
при которых выполняются равенства (1) и
(2). Тогда в силу свойства функции,
непрерывной на некотором отрезке,
функция будет принимать все промежуточные
значения между 0 и 1.
(2) имели корни, т.е. нашлись такие
значения переменной
,
при которых выполняются равенства (1) и
(2). Тогда в силу свойства функции,
непрерывной на некотором отрезке,
функция будет принимать все промежуточные
значения между 0 и 1.
Рассмотрим
уравнение (1):
![]()
![]()
![]()
Таким
образом, уравнение (1) имеет решение при
любых значениях
,
кроме
![]() .
.
Рассмотрим уравнение (2):
![]()
![]()
![]()
![]() .
.
![]() ;
;
![]() ;
;
 .
.
Ответ:
![]() .
.
(ЕГЭ – 04.06.15). Найдите все значения , при каждом из которых система уравнений
 имеет более двух решений.
имеет более двух решений.
Решение.
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
Если
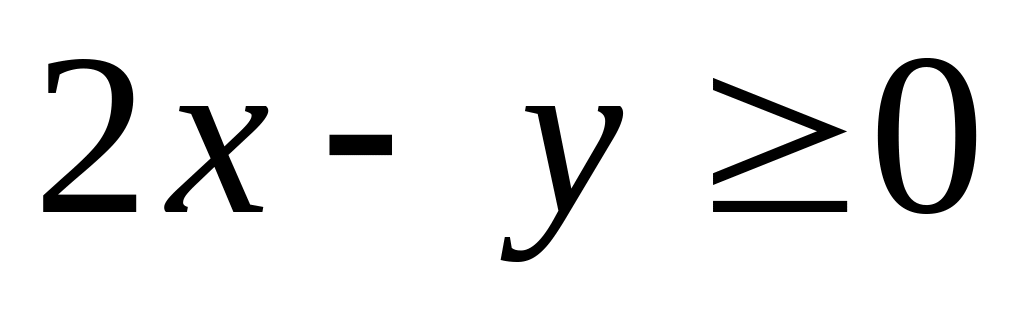 ,
то уравнение имеет вид
,
то уравнение имеет вид
![]() ;
;
![]() ;
;
![]() .
.
Полученное
уравнение задает окружность с центром
![]() и радиусом 5.
и радиусом 5.
Если
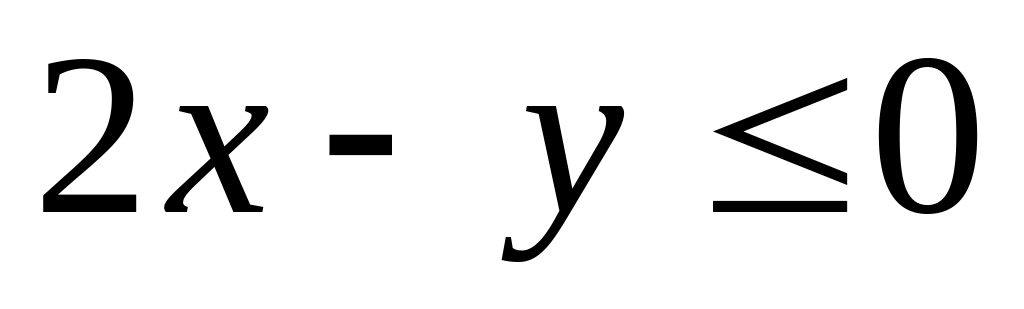 ,
то уравнение имеет вид
,
то уравнение имеет вид
![]() ;
;
![]() ;
;
![]() .
.
Полученное
уравнение задает окружность с центром
![]() и радиусом 5.
и радиусом 5.
Полученные
окружности пересекаются в точках
и![]() ,
лежащих на прямой
,
лежащих на прямой
![]() .
Найдем эти точки:
.
Найдем эти точки:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким
образом, искомое множество состоит из
двух дуг
![]() и
и
![]() с концами в точках
с концами в точках
![]() и
и
![]() .
.
Второе
уравнение системы задает семейство
параллельных прямых
![]() с
угловым коэффициентом
с
угловым коэффициентом
![]() .
Заметим, что эти прямые перпендикулярны
прямой
.
Заметим, что эти прямые перпендикулярны
прямой
![]() и
прямая
и
прямая![]() принадлежит этому семейству (при
принадлежит этому семейству (при
![]() ).
).
Найдем, при каких значениях параметра прямые проходят соответственно через точки и , то есть система имеет три решения:
![]() ;
;
![]() .
.
![]() .
.
Найдем,
при каких значениях
![]() прямые
касаются дуг
и
.
прямые
касаются дуг
и
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Следовательно,
дуги
и
имеют общие касательные. Прямые
касаются дуг
и
при
![]() ,
то есть при этих значениях параметра
система имеет два решения.
,
то есть при этих значениях параметра
система имеет два решения.

Ответ:
![]() ;
;
![]() .
.
(ЕГЭ – 27.09.15). Найдите все значения , при каждом из которых система
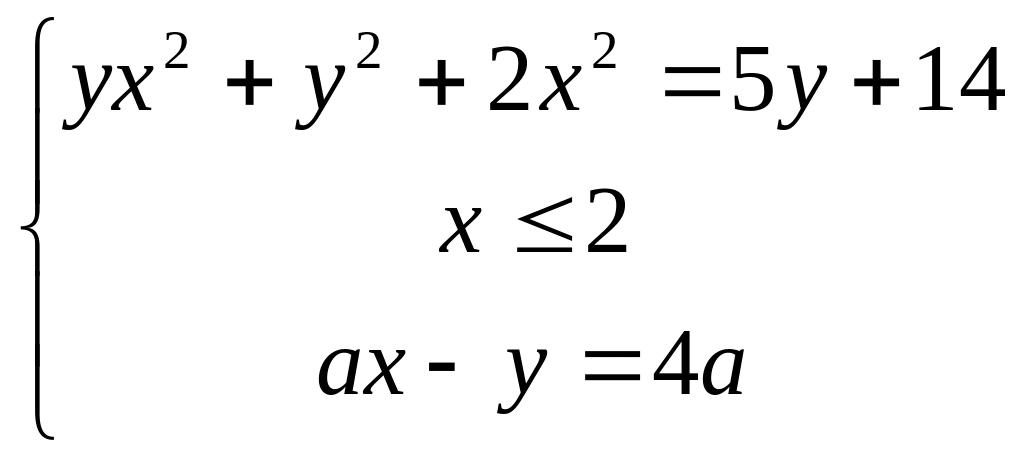 имеет единственное решение.
имеет единственное решение.
Решение.
Запишем первое уравнение в следующем
виде
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
При
уравнение
![]() принимает вид
принимает вид
![]() ,
откуда при
,
откуда при
![]() получаем
получаем
![]() .
С учетом условия
.
С учетом условия
![]() получаем, что при
получаем, что при
![]() и
и
![]() решений нет, а при
решений нет, а при
![]() имеется одно решение.
имеется одно решение.
При уравнение принимает вид
![]() ;
;
![]() .
.
Дискриминант
данного квадратного уравнения
![]() .
.
Таким
образом, уравнение
не имеет решений при
![]() ,
имеет единственное решение при
,
имеет единственное решение при
![]() и при
и при
![]() ,
имеет два решения при
,
имеет два решения при
![]() и
при
и
при
![]() .
При
.
При
![]()
![]() .
.
Таким
образом, при
![]() корни
уравнения
больше 2, поскольку
корни
уравнения
больше 2, поскольку
![]() ,
а минимум квадратичной функции
,
а минимум квадратичной функции
![]() достигается при
достигается при
![]() ;
при
;
при
![]() корни уравнения
не превосходят 2, поскольку
корни уравнения
не превосходят 2, поскольку
![]() ,
а минимум квадратичной функции
,
а минимум квадратичной функции
![]() достигается при
достигается при
![]() ;
при
;
при
![]() только один из двух корней уравнения
не превосходит 2 , поскольку
только один из двух корней уравнения
не превосходит 2 , поскольку
![]() .
.
Определим
значения
,
при которых возможны совпадения решений
из двух разобранных выше случаев. Имеем:
![]() ,
откуда
,
откуда
![]() или
или
![]() .
Случай
не
рассматривается, поскольку
.
Значит,
.
Случай
не
рассматривается, поскольку
.
Значит,
![]() .
.
Таким
образом, исходная система не имеет
решений при
![]() ,
имеет единственное решение при
;
,
имеет единственное решение при
;
![]() ;
и
,
имеет два решения при
;
и
,
имеет два решения при
![]() ;
;
![]() и
и
![]() .
.
Ответ: ; ; ; .
-
Содержание критерия
Баллы
Обоснованно получен правильный ответ
4
С помощью верного рассуждения получено множество значений , отличающееся от искомого только включением /исключением точек ,
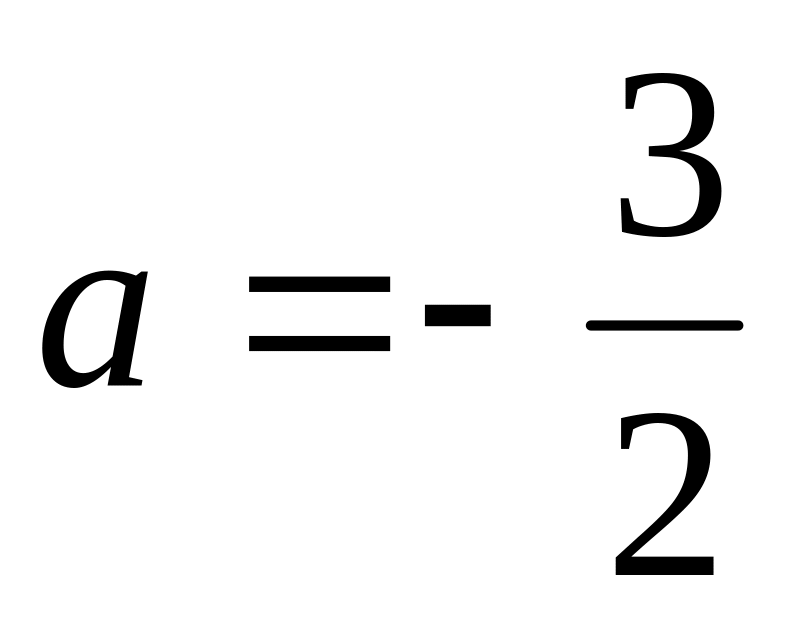 ,
,
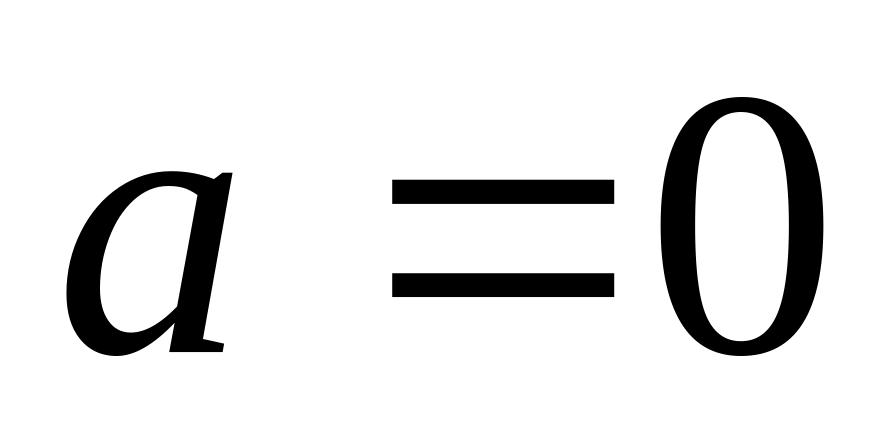 и/или
и/или
3
С помощью верного рассуждения получен один из промежутков множества :
 или
;
возможно, с включением граничных
точек
или
;
возможно, с включением граничных
точек2
Верно найдено хотя бы одно из значений : , или ; или получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
1
Решение не соответствует ни одному из критериев, перечисленных выше.
0
Максимальный балл
4
