Если Вы справились с этой задачей, попробуйте разобраться с задачей о полете баллистической ракеты:
Баллистической ракете сообщается скорость Vст под углом α к горизонту. Нужно определить дальность и время полёта.
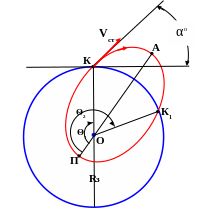
Рис. 6
На рисунке 6 представлена траектория полета баллистической ракеты.
Решение подобной задачи традиционно: по заданному радиусу вектору точки старта (R З) стартовой скорости (V ст ) определяем уже известным путем величину большой полуоси орбиты, по которой будет лететь ракета, и период её абстрактного обращения вокруг центра Земли. Это соотношения, которые известны нам как «интеграл энергии» и «обобщённый третий закон Кеплера».
-
интеграл энергии.
Применительно к нашему случаю, он запишется:
Так как ракета стартует с поверхности, то радиус вектор точки старта равен радиусу Земли. Из этого выражения мы находим большую полуось орбиты.
Далее, из третьего обобщённого закона Кеплера определяем период её «обращения» вокруг центра Земли – Т .
Т2/а3 = 4π2/GM = 4π2/ K
Дальнейшее решение отличается от того, как мы поступали в предыдущих задачах. В этом случае нам неизвестны (в отличие от предыдущих задач) ни перигейное, ни апогейное расстояния. Следовательно, нельзя определить эксцентриситет «орбиты» и все остальные характеристики полета ракеты.
В этом случае используем ещё один закон сохранения – закон сохранения момента импульса:
Попробуем применить этот закон к двум точкам орбиты – к точке старта и к точке перигея (можно и апогея).
Радиус вектор точки перигея равен радиусу Земли. Скорость ракеты в этой точке – это стартовая скорость. Направление радиуса вектора – от центра Земли и далее. Значит, укол между этими двумя векторами не α , а (90о- α) .
Тогда момент импульса ракеты в точке старта будет равен:
m × (RЗ× Vст×cos(90 – α)) = m × RЗ × Vст×sin α
Обе части уравнения можно сократить на массу ИСЗ - m
В точке перигея вектор скорости Vq направлен под углом 90 градусов к радиусу вектору (q) этой точки. Значит sin α =1. Момент импульса ракеты в точке перигея будет равен (см. соотношения 1 и 5) :
m × (q × Vq) = m × a(1-e)×(2πa/T×((1+e)/(1-e))0,5 = m × 2πа2(1-e2)0,5/T
Приравнивая значения моментов импульса ракеты в точках старта и перигея и сокращая обе части уравнения на массу ИСЗ – m, получим уравнение с одним неизвестным – е – эксцентриситетом:
RЗ × Vст×sin α = 2πа2(1-e2)0,5/T
Отсюда находим величину эксцентриситета и далее последовательно величины q, q, Hq , hq , Vq , vq .
Далее, подобно тому, как мы поступали в последней задаче, определяем истинные, эксцентрические и средние аномалии точек старта и точек падения, используя последовательно уравнения (4), (16), (15) .
На нашем рисунке истинные аномалии точек старта и падения обозначены буквами Θ1 и Θ2 соответственно. По рисунку легко сообразить, что дуга КК1 будет равна Lо = Θ2 - Θ1. Это и есть дальность полета ИСЗ. Мы определили её величину в градусах.
Чтобы выразить её в километрах – Lкм - достаточно вспомнить, что 2π R - длина дуги большого круга на поверхности Земли - соответствует 360 градусам. Значит, зная радиус Земли, можно сосчитать количество километров, приходящихся на один градус или на КК1 градусов.
Зная средние аномалии точек старта и падения, опираясь на соотношение (14):
М = 360о/T×∆t
можно определить - ∆t1 - время «полета» ракеты от перигея до точки старта и ∆t2 - время «полета» ракеты от перигея до точки падения. Тогда время полёта ракеты от запуска до падения будет равно:
∆Т = ∆t2 - ∆t1
Пробная задача № 4
Баллистической ракете сообщается скорость Vст = 8 км/сек. под углом α = 30 градусов к горизонту. Нужно определить все характеристики движения ракеты, дальность и время её полёта.
Если Вы всё рассчитали правильно у Вас должно получиться, что L = 13912 км., время полёта ∆Т = 5269 сек., или 1час. 27мин. 49сек.
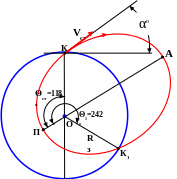После этого, осталось нарисовать
рисунок с примерным соблюдением всех
параметров полета:
Рис. 7
После того, как Вы справились со всеми пробными задачами, можно взять у преподавателя контрольную задачу. Правильное решение контрольной задачи будет расцениваться как зачёт по данноё лабораторной работе.