Ход выполнения работы:

При решении задач мы будем считать известными следующие величины:

R_  = 6.378  10⁶ м. - радиус Земли;

М_ = 5,97  10²⁴ кг. – масса Земли;

G = 6.63  10^-11 – постоянная тяготения (СИ).

Пробная задача 1

Задана стартовая скорость V_{ст. =} 8 км/с., направленная параллельно к поверхности Земли и H_ст = 500 км. – стартовая высота. Определите все, какие сможете, характеристики его движения, и положение спутника на орбите через 30 минут после старта. Так же в этот момент необходимо определить его высоту над поверхностью Земли и скорость.

Ниже подробно описан ход решения задачи, с описанием наиболее часто встречающихся ошибок, но значения всех рассчитанных величин не приводятся. Будут приведены только координаты ИСЗ через 30 минут после старта, его высота и скорость. Если результаты Ваших расчетов совпадут с приведёнными, значит всe остальные величины определены правильно.

Стандартное начало решения – это использование соотношения (7).

Применительно к нашему случаю (к точке старта):

V – стартовая скорость,

r = R_  + H_ст – радиус- вектор точки старта ;

а – большая полуось орбиты, по которой будет двигаться ИСЗ.

Из этого соотношения выразим большую полуось – а - и найдем ее.

Знание величины большой полуоси позволяет сразу определить из третьего обобщённого закона Кеплера период обращения ИСЗ вокруг Земли:

Т²/а³ = 4π²/GM = 4π²/ K

Чаще всего при определении большой полуоси и периода, численные значения используемых величин подставляют в разных системах единиц. Естественно, что при этом получаются совершенно невероятные результаты. Поскольку величину постоянной тяготения (и гравитационного параметра Земли) мы знаем в СИ, поэтому и остальные величины должны быть подставлены только в этой же системе единиц.

Далее, опираясь на рис. 1 и приводимые там соотношения, определяем перигейное расстояние – q, апогейное расстояние - Q, высоты в апогее и перигее - H_q и H_Q . Прежде чем присваивать конкретные численные значения H_{q ,}H_Q , q и Q , Вы должны понять, что точка старта, в зависимости от величины стартовой скорости может быть как перигеем, так и апогеем. Поэтому, прежде чем присваивать значения этим величинам, опираясь на уже известные значения α, R_ и H_ст , определите высоту ИСЗ в противоположной точке - H_{пр. .}

Дальнейшее решение задачи будет зависеть от того, какова величина Н_пр. Существует три возможные варианта, определяющие особенности дальнейшего решения задачи:

1. Если: Н_пр> Н_ст значит, спутник вышел на орбиту, и противоположная точка является точкой апогея, а точка старта – точка перигея;

2. Если: Н_пр< Н_ст значит, точка старта – точка апогея, противоположная точка – точка перигея.

3. Если: Н_пр< 0 значит, спутник не вышел на орбиту и упал;

В случае нашей пробной задачи стартовая скорость задана такой, что точка старта является перигеем. Это первый вариант этой задачи. Значит H_q = H_ст , q = R_з+ H_{ст ,} Q = R_з+ H_пр = R_з+ H_Q .

_{Только после этого можно рассчитать величину эксцентриситета, правильно выбрав нужное из двух соотношений:} (1) _или (2) . Если точка старта является точкой перигея, значит при определении эксцетриситета, будем пользоваться соотношением (1), которое применительно к такому случаю запишется:

q = R + H_ст= a×(1-е);

Далее, используя соотношения (5) и (6), находим значения перигейной и апогейной скоростей V_q и V_Q .

Последний этап решения этой задачи – определение положения ИСЗ на орбите через 30 минут после старта. Это значит, что нужно рассчитать полярные координаты ИСЗ: Θ – истинную аномалию и r – радиус вектор в этот момент времени.

Для этого, прежде всего, рассчитываем среднюю аномалию ИСЗ через 30 минут после старта:

М = 360^о/T×∆t (14)

Здесь:

М – средняя аномалия ИСЗ;

Т – период обращения спутника вокруг Земли;

∆t – промежуток времени, прошедший от момента нахождения ИСЗ в перигее до интересующего нас момента. В нашем случае это 30 мин.

Найденное значение М используем для определения эксцентрической аномалии спутника – Е. С дальнейшим Вы уже встречались при выполнении лабораторной работы № 2. Связь между эксцентрической и средней аномалиями задается уравнением Кеплера:

E = M +57^о,296 × e× sin E (15)

Здесь:

57^о,296 – величина одного радиана в градусах;

е – эксцентриситет орбиты ИСЗ.

Уравнения такого типа называются трансцендентными – неизвестная нам величина - Е - присутствует и под знаком тригонометрической функции. Такие уравнения решаются методом последовательных приближений. Первое приблизительное решение - Е1 – находим, подставляя под знак тригонометрической функции синуса найденную нами ранее величину средней аномалии - М :

E1 = M + 57^о,296× e× sin М

Втрое приблизительное решение находим, подставляя под знак синуса величину Е1:

E2 = M + 57^о,296 ×e× sin Е1

Совершенно аналогично находим третье, четвёртое и т.д. приближения.

Мы получим ряд сходящихся значений. Такие вычисления будем производить до тех пор, пока разница между двумя последними приближениями не будет меньше или равна нужной нам точности расчётов. Мы договорились все значения углов рассчитывать с точностью 0^о,1. Значит, вычисления будем продолжать до тех пор, пока разница между двумя последними приближениями не будет меньше (или равна) 0^о,1. Последнее из приближений считаем окончательным.

После этого рассчитываем первую полярную координату ИСЗ на нужный нам момент – Θ – истинную аномалию.

tg (Θ/2) = [(1+e)/(1-e)]^0,5 ×tg (E/2) (16)

Радиус вектор спутника рассчитываем исходя из уравнения эллипса в полярных координатах (4):

r = [a×(1 - e²)] / [1 + (e×cosΘ)]

Радиус вектор спутника в какой-то момент – это сумма радиуса Земли и высоты ИСЗ над её поверхностью в данный момент:

r = R_  + H

Отсюда находим H - высоту спутника над землёй.

Последний этап решения – это определение скорости ИСЗ в этой точке.

Для этого воспользуемся интегралом энергии (7). Используя это выражение, рассчитаем скорость ИСЗ в точке с найденным значением радиуса вектора.

Если Вы всё сосчитали правильно, Вас должно получиться:

Θ = 108,3

r = 7821 км.

H = 1443 км.

V = 7,7 км/сек.

Последнее что осталось сделать – это нарисовать рисунок с примерным соблюдением масштаба и положением ИСЗ на орбите :

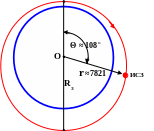
Рис 2

На этом заканчивается решение данной задачи, в которой высота спутника в противоположной точке оказалась больше стартовой высоты: Н_пр> Н_ст .

Рассмотрим сейчас ситуацию (это второй вариант нашей задачи) при которой высота ИСЗ в противоположной точке меньше стартовой высоты: Н_пр< Н_ст . Это значит, что точка старта – точка апогея, противоположная точка – точка перигея.

Ход решения такой задачи подобен решению предыдущей задачи с двумя существенными отличиями, непонимание которых приводит к не верным результатам.

Первое, что необходимо понять, что в таком случае, что при определении эксцентриситета нужно пользоваться соотношением (2), которое в таком случае запишется:

Q = R + H_ст = а×(1+е);

Второе понять значительно труднее. Оно касается определения положения ИСЗ на орбите через какой-то промежуток времени ∆t после старта. Дело в том, что все три угла: M - средняя аномалия, E - эксцентрическая аномалия и Θ - истинная аномалия измеряются от направления на точку перигея. А это не точка старта, а противоположная точка. Именно она будет точкой перигея. Это

значит, что если мы желаем в таком случае найти положение ИСЗ на орбите через ∆t после старта, в соотношение (14) нужно подставлять величину ∆t₁ - время, прошедшее после прохождения ИСЗ не точки старта, а точки перигея:

∆t ₁ = ∆t + Т/2

Здесь:

Т/2 - полупериод обращения ИСЗ вокруг Земли. Именно столько