Задача о наименьшей поверхности вращения
Пусть даны две точки
,
плоскости
,
пусть
.
Пусть далее
– уравнение кривой, соединяющей точки
и
,
т.е.
,
.
Кривая вращается вокруг оси
,
заметая некоторую поверхность вращения.
Спрашивается, что представляет собой
поверхность вращения, имеющая наименьшую
возможную площадь. Таким образом, мы
приходим к проблеме выбора функции
,
для которой интеграл
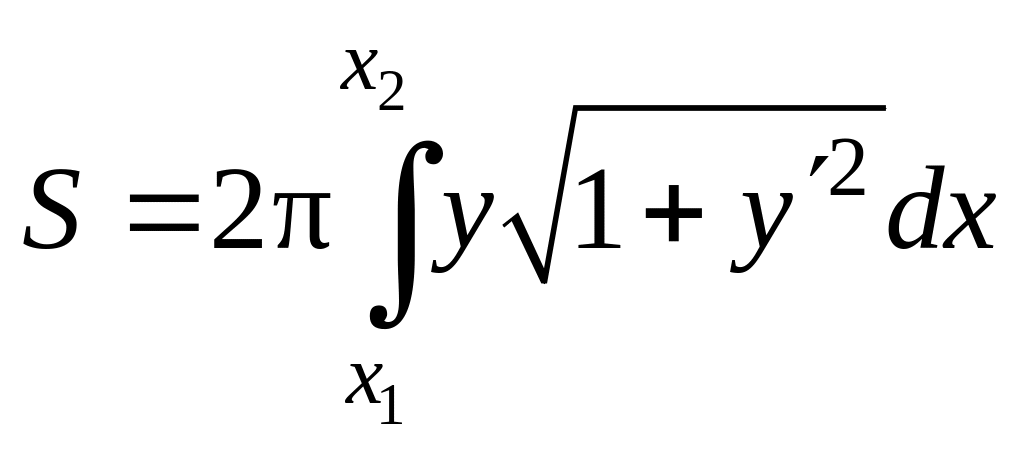
– площадь поверхности вращения – минимален. Такие минимальные поверхности вращения, при некоторых дополнительных ограничениях на точки и , называются катеноидами.
Функция F в этом случае
имеет вид
,
то есть не зависит от x. Первый
интеграл дается равенством
,
и тогда
.
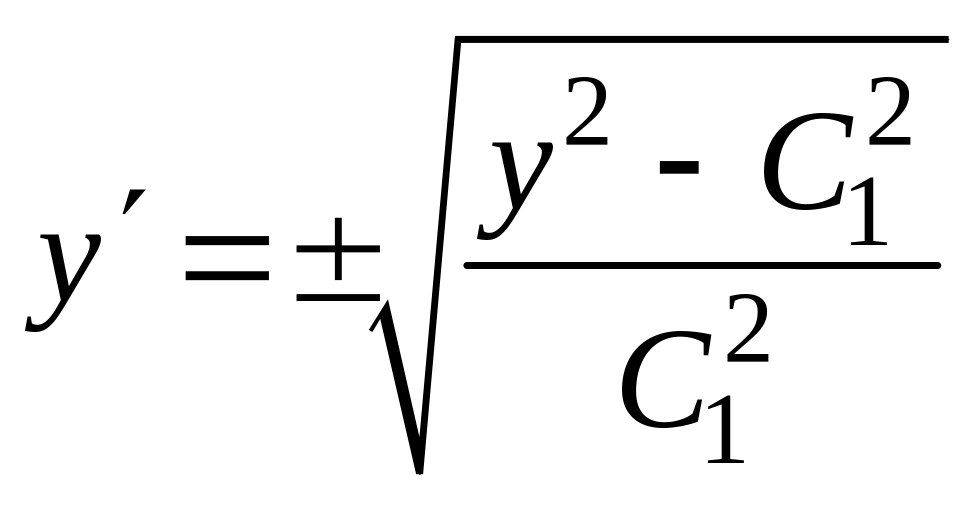Решая это уравнение в разделяющихся переменных, получаем
.
Удобно далее положить
.
Тогда
.
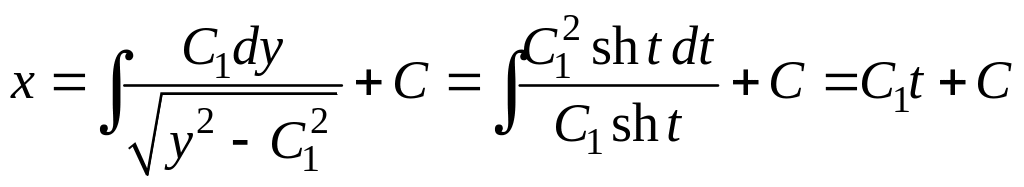Положим
и
,
тогда окончательно
– искомая кривая (цепная линия).
Список рекомендуемой литературы
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. – М.: Эдиториал УРСС, 2000. – 319 с.
Романко В.К. Курс дифференциальных уравнений и вариационного исчисления / В.К. Романко. – М., СПб.: Физматлит, 2000. – 342 с.
Пантелеев А.В. Вариационное исчисление в примерах и задачах / А.В. Пантелеев. – М.: Изд-во МАИ, 2000. – 227 с.
Варианты заданий Задание 5
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
,
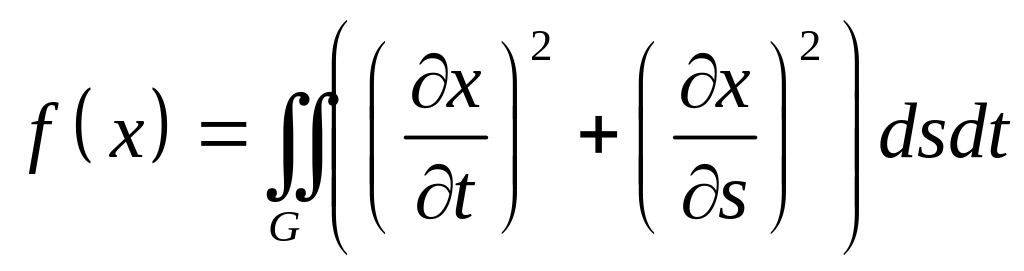– сектор круга:
.
Граничные условия:
,
.
,
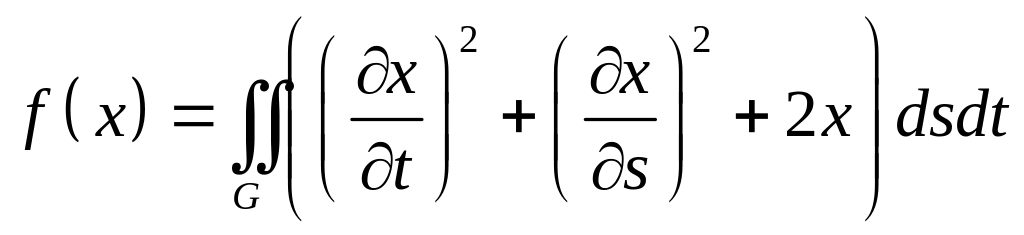– кольцо:
.
Граничные условия:
,
.
,
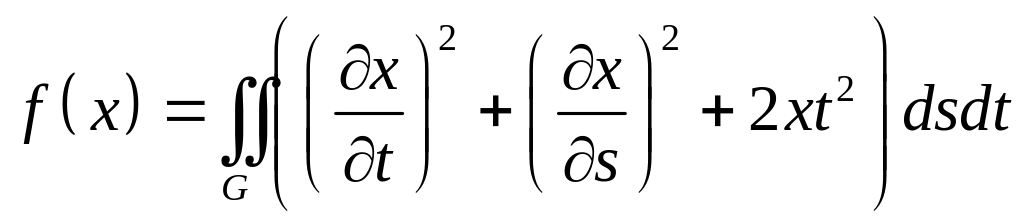– круг:
.
Граничные условия:
.
,
– квадрат:
.
Граничные условия:
,
.
,
– сектор кольца:
.
Граничные условия:
,
.
,
– сектор круга:
.
Граничные условия:
,
.
,
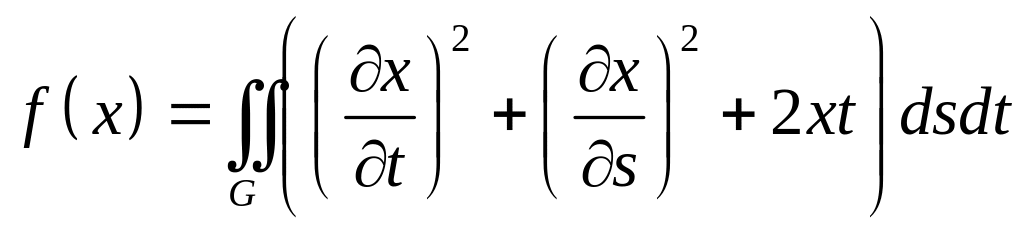– кольцо:
.
Граничные условия:
,
.
,
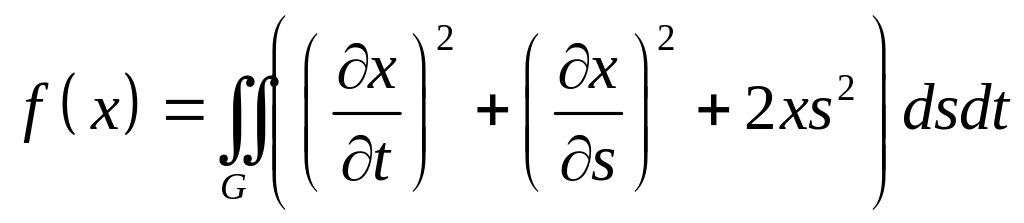– круг:
.
Граничные условия:
.
,
– квадрат: .
Граничные условия:
,
.
,
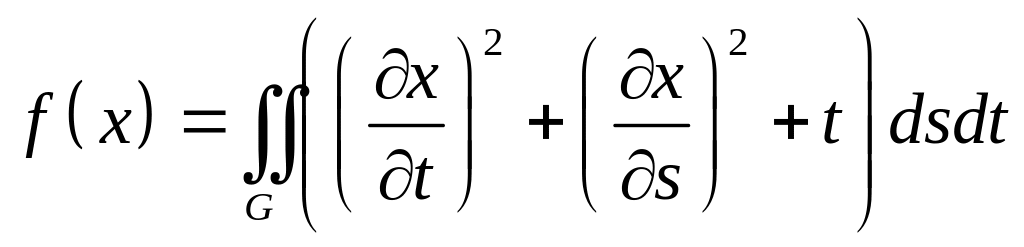– сектор кольца:
.
Граничные условия:
,
.
,
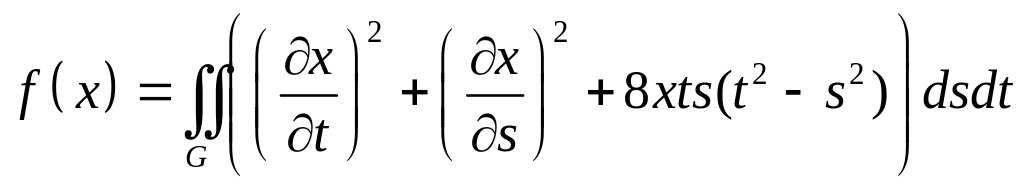– сектор круга:
.
Граничные условия:
,
.
,
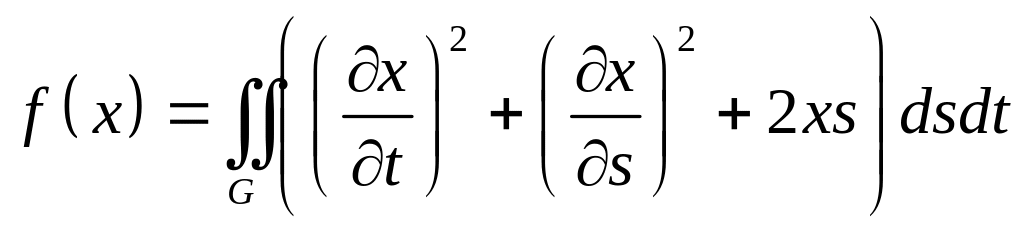– кольцо:
.
Граничные условия:
,
.
,
– круг:
.
Граничные условия:
.
,
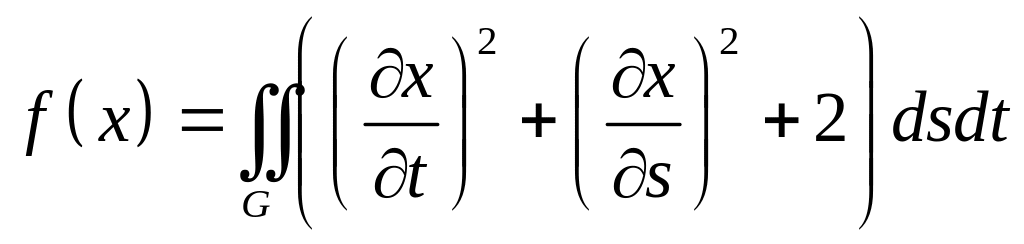– квадрат: .
Граничные условия:
,
,
.
,
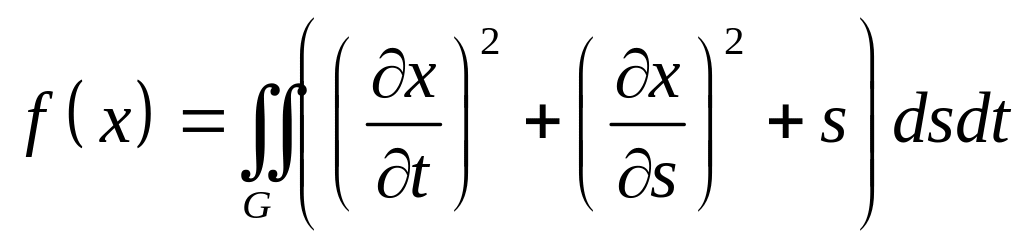– сектор кольца:
.
Граничные условия:
,
.
,
– сектор круга:
.
Граничные условия:
,
.
,
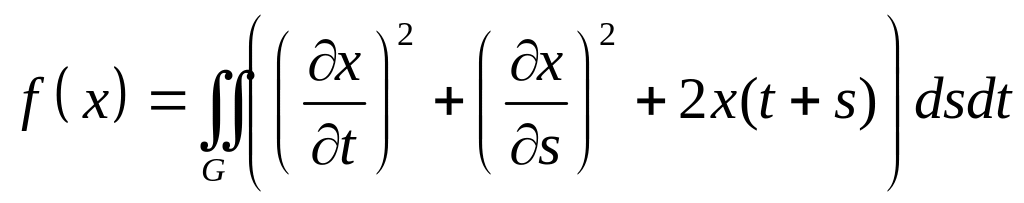– кольцо: .
Граничные условия:
,
.
,
– круг: .
Граничные условия:
.
,
– квадрат: .
Граничные условия:
,
,
.
,
– сектор кольца: .
Граничные условия:
,
.
,
– сектор круга:
.
Граничные условия:
,
.
,
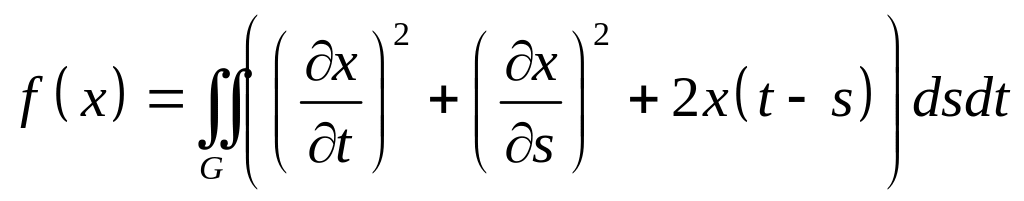– кольцо: .
Граничные условия:
,
.
,
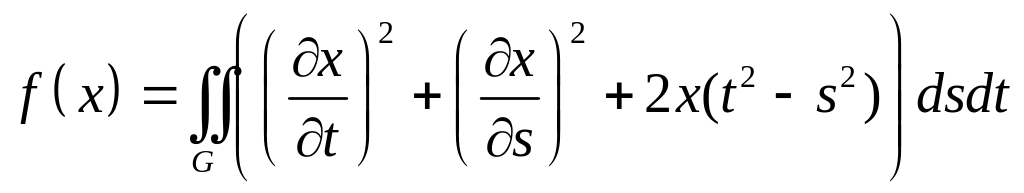– круг: .
Граничные условия:
.
,
– квадрат: .
Граничные условия:
,
,
.
,
– сектор кольца:
.
Граничные условия:
,
.
,
– сектор круга:
,
.
Граничные условия:
,
,
где
– произвольная непрерывная на отрезке
функция.
,
– кольцо: .
Граничные условия:
,
.
,
– круг: .
Граничные условия: .
,
– квадрат: .
Граничные условия:
.
,
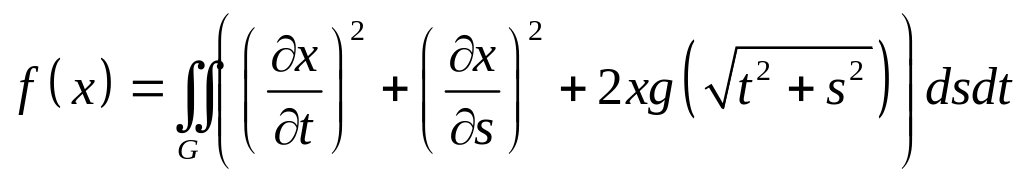– сектор кольца:
,
– непрерывная на отрезке
функция.
Граничные условия:
.